Данный подход лежит в основе ряда методов контроля качества, используемых в промышленности и производстве. Доверительные пределы служат ориентиром в том, что касается ожидаемого диапазона для конкретных переменных. Любое значение, оказавшееся в ходе исследования за пределами этого [c.86]
Кроме 95%-ных пределов, иногда при некоторых обстоятельствах используются и другие доверительные пределы, например [c.87]
Оставляем вам возможность рассчитать 99.8%-ные доверительные пределы для данного распределения. [c.87]
Использование альтернативных доверительных пределов важно при решении задач, требующих большей или меньшей степени точности. Например, избыточный или недостаточный вес упаковки с шоколадом не столь важен, сколь отклонения в весе основных химических компонентов лекарственного препарата. Таким образом, различные доверительные пределы используются в соответствии с важностью рассматриваемой переменной. [c.87]
Т Определение. Доверительные пределы определяют верхнее и нижнее значения, между которыми помещается центральная пропорция от совокупности. Например, 95%-ные доверительные пределы определяют границы, в пределах которых находится 95% всех возможных значений. А [c.87]
По таблице нормального распределения находим, что выделенный участок равен 0.10565. Таким образом, существует вероятность в 10.565% того, что выборочная средняя превышает 405 г. На основании той же самой информации мы можем рассчитать ожидаемую вариацию для выборочных средних. Например, при условии нормального распределения 95%-ные доверительные пределы для выборочных средних рассчитываются следующим образом [c.88]
Далее, для данной совокупности 95%-ные доверительные пределы значений выборочных средних определяются по формуле 2500 + 1.96 х 42.43 = 2500 + + 83.16 = от 2416.8 до 2583.2 изделия. [c.89]
Гипотеза проверяется путем рассмотрения того, является ли полученная выборочная средняя значимой , иначе говоря, находится ли это значение вне доверительных пределов. Вместо вычисления доверительных пределов и сравнения их с полученным значением мы можем пойти по другому пути. Необходимо только провести расчеты по следующей формуле [c.90]
Это значение затем можно сравнить с таким критическим значением, как 1.96, если мы берем 95%-ные доверительные пределы. Таким образом, в данном примере [c.91]
Итак, значение z (= 1) меньше 1.96 и поэтому не значимо при 95%-ных доверительных пределах. (В том, что касается предыдущего раздела, это означает, что выборочная средняя находится внутри 95%-ных доверительных пределов.) Следовательно, мы можем принять нулевую гипотезу, т. е. мы принимаем Н0. Отсюда следует, что данная выборка не заставила нас усомниться в допущении того, что средний вес изделия составляет 400 г. Таким образом, мы не можем воспользоваться фактами, полученным в ходе данного выборочного обследования, чтобы доказать, что параметры производства не выдерживаются. [c.91]
Значение z затем можно сравнить с 1.96 при 5%-ном уровне значимости, т. е. при 95%-ных доверительных пределах, или же с другими значениями, например 2.58 при 1%-ном уровне значимости, т. е. при 99%-ных доверительных пределах. [c.92]
Н) Если из данной совокупности взять выборку из 100 единиц, то каковы 95%-ные доверительные пределы для выборочного среднего [c.92]
Имеются различные статистические критерии, которые используются для оценки значимости данного значения г. Но их описание выходит за пределы данного пособия. Однако следует сказать, что эти критерии основываются на учете доверительных пределов для значений г Например, можно показать, что при условии отсутствия корреляции между двумя переменными 95%-ные доверительные пределы для значения г, где п = 10, составляют от —0.632 до +0.632. Следовательно, если две переменные не соотносятся вообще, то значение г, вероятно, лежит в указанном диапазоне. Таким образом, для того чтобы указать на значимость корреляции между двумя переменными, значение г должно оказаться вне этого диапазона, т. е. быть больше +0.632 или меньше —0.632. [c.113]
В таблице на рис. 3.7 приведены значимые значения г для п значений и 95%-ных доверительных пределов. Обратите внимание, что значения г могут быть как положительными, так и отрицательными. Из этой таблицы видно, что по мере увеличения объема выборки (п), критическое значение г уменьшается. Так, например, для = 3 значение г должно быть минимум 0.997, чтобы мы могли сделать вывод о наличии корреляции между двумя переменными. А при объеме выборки п = 100 значение г свыше 0.19 указывает на весьма слабую корреляцию. [c.113]
В этой ситуации мы должны установить, является ли значение г = 0.6, полученное при объеме выборки п = 10, значимым. Согласно таблице на рис. 3.7, значение г для этого объема выборки составляет 0.632. Следовательно, значение г (=0.6) не считается значимым при условии 95%-ных доверительных пределов. Таким образом, данная величина не является убедительным доказательством того, что имеется зависимость между расходами на рекламу и месячным объемом выручки от реализации. Однако значение / столь близко к значимому , что, вероятно, между данными показателями все же существует зависимость. Необходим сбор дополнительной информации, как-то о расходах на рекламу и объеме выручки от реализации за более продолжительный период времени. [c.114]
И) Будет ли эта корреляция значимой при 95%-ных доверительных пределах Каковы ваши выводы по итогам анализа относительно пригодности собеседования в процессе отбора [c.116]
В главе рассмотрен анализ зависимости между двумя или более наборами значений. Графики разброса можно использовать для иллюстрации любой связи между двумя переменными. Однако результаты, полученные из таких графиков, существенно субъективны. Для последующего и углубленного анализа зависимости необходимо использовать объективный показатель. Одним из таких показателей является линейный коэффициент корреляции, который оценивает близость соотношения двух переменных. Этот коэффициент, обозначаемый г, измеряет степень корреляции, или линейной зависимости, между двумя переменными. Значение коэффициента корреляции лежит в пределах от —1 до +1. Значения г, близкие к + 1 или — 1, указывают на наличие сильной зависимости между двумя переменными. И наоборот, значения, близкие к нулю, показывают, что зависимость мала. Фактические значения линейного коэффициента корреляции, которые указывают на наличие значимой корреляции, зависят от объема выборки. Так, коэффициент корреляции г= 0.8 при выборке из 10 пар значений менее значим, чем линейный коэффициент корреляции, равный г — 0.7, при выборке из 100 значений. Значимость коэффициента можно подтвердить с помощью доверительных пределов. Коэффициент детерминации, вычисляемый путем возведения в квадрат значения коэффициента корреляции, также можно использовать для определения зависимости между переменными. [c.128]
Это значение в определенной степени указывает на точность примененной модели прогнозирования. Малое значение среднеквадратического указывает на большую надежность прогнозной модели. Среднеквадратическое можно использовать для оценки доверительных пределов любого прогноза. Это значение можно применять как оценочный показатель среднеквадратического отклонения, и при условии того, что ошибки образуют нормальное распределение, 95%-ные доверительные пределы для фактического значения, основанного на прогнозе F, определяются следующим образом [c.213]
То есть при вычислении доверительных пределов мы берем формулу для нормального распределения, описанную во второй главе. Данная формула также предполагает отсутствие смещения в модели прогнозирования. Так, при большом объеме выборки средняя ошибка оказалась равной нулю. Если она не равна нулю, то остаточный член также необходимо включить в формулу определения доверительных пределов. [c.213]
Итак, давайте предположим, что в нашем примере согласно полученному прогнозу в какой-то из дней за помощью обратится 40 пациентов. Следовательно, мы можем вычислить 95%-ные доверительные пределы [c.213]
Итак, рассмотрим прогноз в 90 тонн в качестве объема производства на следующий период. Если предположить, что ошибки образуют нормальное распределение со средним, равным нулю, то доверительные пределы для значений фактического объема производства рассчитываются следующим образом [c.214]
Далее, целесообразно оценить показатель разброса (среднеквадратическое отклонение) с тем, чтобы проанализировать возможный разброс в продолжительности всего проекта. Методы нормального распределения, описанные в главе 3, позволяют оценить среднеквадратическое отклонение (ст) исходя из диапазона 99.8% доверительные пределы равняются приблизительно ц + Зст, что показано на графике на рис. 10.36. То есть три среднеквадратических отклонения в любую из сторон от среднего фактически захватят все из значений распределения. [c.380]
| Рис. 10.36. Доверительные пределы нормального распределения | 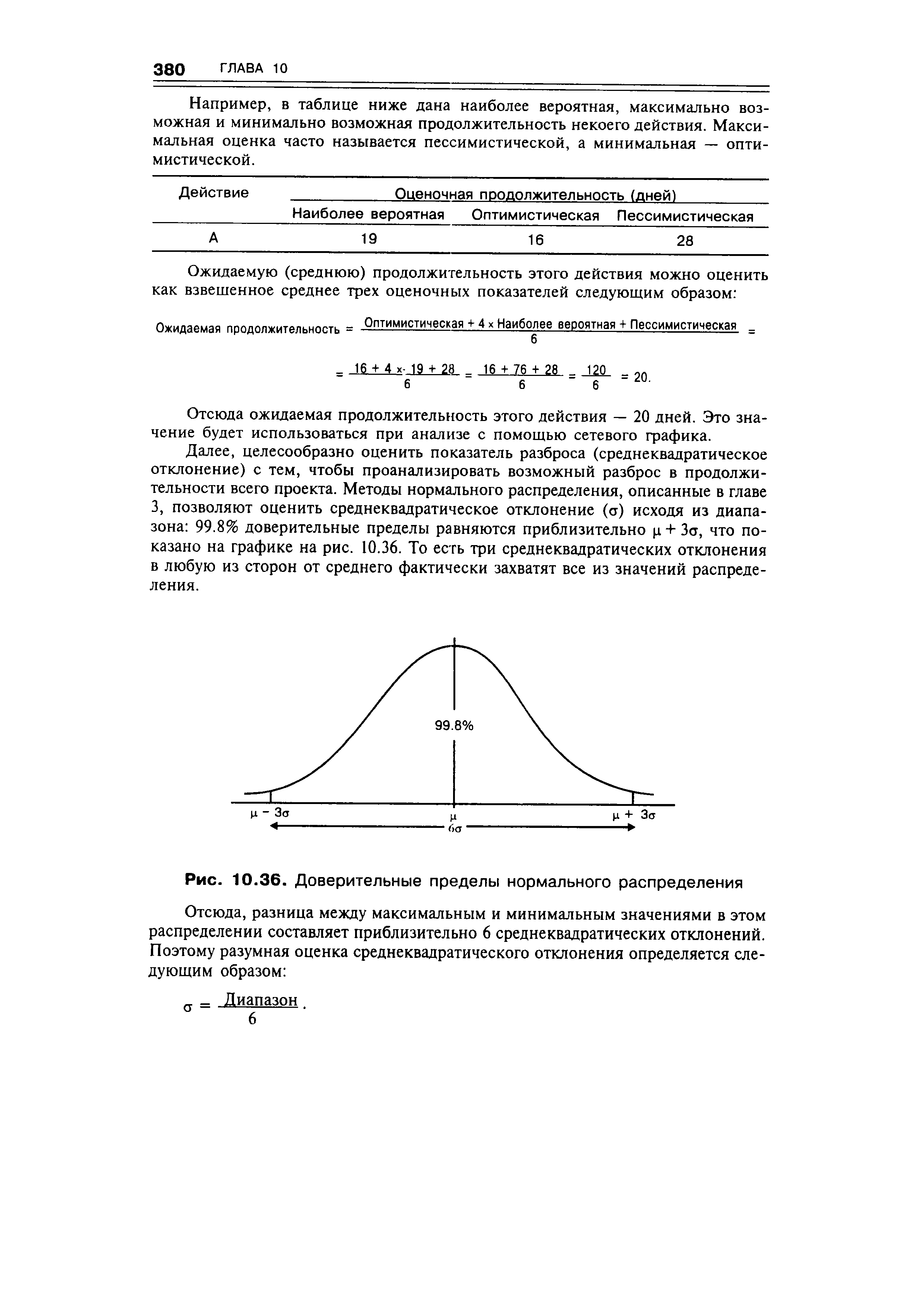 |
Стандартное отклонение Доверительный предел [c.406]
Например, менеджеры могут пожелать узнать, с определенной степенью доверия, вероятность того, что потоки средств сократятся ниже некоего уровня. (Термин "доверительные пределы" — это то же, что процент случаев, охватываемых при тех или иных стандартных отклонениях.) Очевидно, что необходимость выполнить обязательства по возврату ссуды предполагает некое минимальное поступление средств в результате операций. Если предположить, что кредитора интересует только один край распределения (нижняя часть), а вся верхняя часть распределения над средней (где фирма превышает минимум средств) не внушает беспокойства, каждый уровень стандартного отклонения внушает больше доверия, чем указано выше. [c.407]
Но если кредитор стремится быть более уверенным в том, что он предвидел все возможные события, он должен выбрать больший доверительный предел. При трех стандартных отклонениях и 10 наблюдениях (см. табл. 9.4) аналитик может быть на 99% уверен в том, что он учел все возможности. Умножив 12,83% на 3, аналитик устанавливает, что, если он хочет быть уверенным в погашении задолженности на 99%, способность фабриканта возвращать долг необходимо снизить до 61,51% (100% — 38,49%). [c.416]
Данный метод можно приспособить для вычисления доверительных пределов. Такие пределы обозначают диапазон значений, который содержит заданную пропорцию от общего количества значений вокруг среднего арифметического. Например, 95%-ные доверительные пределы в нормальном распределении можно получить по формуле ц 1.9а. Эти пределы, показанные на рис. 2.24, определяют два значения, между которыми помещаются центральные 95% значений распределения. Таким образом, шлейфовые участки, соответственно слева и справа от данных значений, составляют только 2.5% от общей площади каждый. Для такого шлейфового участка значение z из таблицы равно 1.96. Следовательно, значение z = (х — ц)/о = 1.96. Таким образом, имеем х — ц = = 1.96а и отсюда х = ц. + 1.96а. Аналогично получаем нижний предел, который равен ц — 1.96ст. [c.86]
Например, 95%ст доверительные пределы для веса упаковок с шоколадом производства компании Даунбрукс , где средний вес составляет 400 г, а сред-неквадратическое отклонение — 20 г, равны ц+ 1.9а = 400 + 1.96 х 20 = 400 + 39.2, или от 360.8 до 439.2 г. Итак, мы можем быть на 95% уверены, что вес упаковки с шоколадом находится в пределах от 360.8 до 439.2 г. [c.86]
Так, например, 99%-ные доверительные пределы для веса упаковки шоколада (сходный пример мы уже рассматривали) составляют ц 2.58ст = 400 + 2.58 х 20 = 400 + 51.6, т. е. от 348.4 до 451.6. [c.87]
И) Найдите 95%-ные доверительные пределы для среднего количества заказов, полученных за этот десятинедельный период. [c.93]
Смотреть страницы где упоминается термин Доверительные пределы
: [c.68] [c.69] [c.52] [c.52] [c.85] [c.86] [c.87] [c.87] [c.92] [c.92] [c.94] [c.95] [c.222] [c.385] [c.395] [c.396] [c.418]Смотреть главы в:
Количественные методы анализа хозяйственной деятельности -> Доверительные пределы
