| Рис. 10.5. Кривая нормального распределения Гаусса для значений функций долевого участия собственных средств | 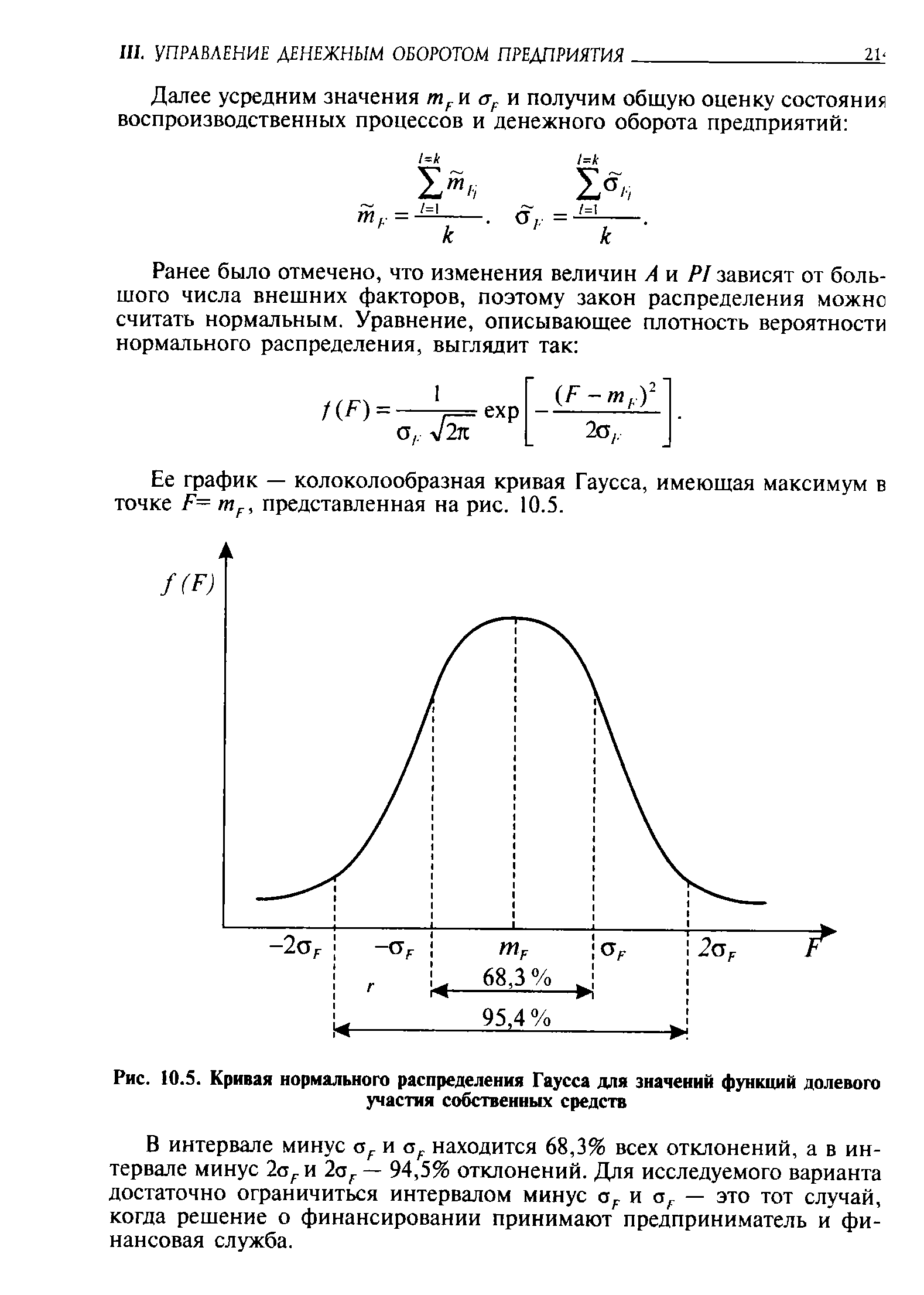 |
Распределение имеет вид симметричной колоколообразной кривой, распространяющейся по всей числовой оси. Распределение Гаусса зависит от двух параметров (//, сг). [c.34]
Плотность вероятности распределения Гаусса нельзя проинтегрировать для получения интегральной функции распределения вероятностей F(x) в явном виде. F(x) можно найти с использованием [c.35]
Распределение Гаусса можно использовать в качестве первого приближения для описания, например, логарифмов относительного изменения цен активов. Однако, только в качестве первого приближения, потому что на практике распределения этих величин отличаются от нормального, то есть имеют как правило более ярко выраженный пик и более "тяжелые" хвосты. Следовательно эти распределения являются островершинными и имеют эксцесс, превышающий три (иногда очень существенно). [c.35]
Параметры логнормального распределения выражаются через параметры соответствующего распределения Гаусса следующим образом [c.37]
Как и в случае распределения Гаусса, плотность вероятности логнормального распределения нельзя проинтегрировать [c.37]
Однако, значения интегральной функции логнормального распределения можно найти, используя значения интегральной функции распределения Гаусса, так как они связаны соотноше- [c.38]
Логнормальное распределение можно использовать в качестве первого приближения для описания относительного изменения цен активов, однако, с теми ограничениями, о которых было сказано при обсуждении распределения Гаусса. [c.38]
Как и распределение Гаусса, распределение Лапласа зависит от двух параметров (//, сг), [c.38]
Казалось бы, распределение Коши выглядит очень привлекательно для описания и моделирования случайных величин. Однако в действительности это не так. Свойства распределения Коши резко отличны от свойств распределения Гаусса, Лапласа и других экспоненциальных распределений. [c.39]
Выше в этой главе были рассмотрены два вида экспоненциальных распределений Гаусса и Лапласа. У них много общего они симметричны, зависят от двух параметров (//, сг), [c.41]
Обычно в справочниках распределения Гаусса, Лапласа и равномерное рассматриваются как разные распределения, хотя в излагаемой здесь концепции - это одно и тоже распределение. Единственным параметром, характеризующим форму (а значит и свойства) этих распределений является показатель ОС. [c.42]
Исходные данные к распределению Гаусса [c.44]
Сравнивая результат подсчета с критическим значением квантиля распределения Гаусса ta = 1,96 (J < ta) при ос = 0,05 [92], приходим к выводу о возможности принятия гипотезы. [c.46]
Пример 3.1. Оценка смещения центра группирования. В период отладки технологического процесса было установлено, что параметр изделия, который оказывает существенное влияние на качество готовой продукции, имеет распределение Гаусса с параметрами X - 50,20 мм 5 = 2,10 мм. Объем выборки п, по которой определяли эти значения, равен 300. [c.64]
Прежде всего найдем значение энтропии распределения Гаусса, соответствующее отлаженному производству. Для этого определим вначале вероятности [c.65]
Распределение Пирсона при m > 25 можно заменить распределением Гаусса с дисперсией а/ = 2т [52], что дает возможность определить доверительный интервал для информации [c.74]
В период отладки технологического процесса было установлено, что параметры Хи 7 имеют распределение Гаусса с параметрами х = 52,2 мм, [c.102]
Можно отметить, что параметры № 13, 16 имеют распределение Гаусса № 3,7 — распределение Рэлея № 10, 17 — распределение Максвелла №1,2, 4, 5, 8, 9, 11, 12, 14, 15 имеют одностороннее нормальное распределение. [c.148]
Согласившись с тем, что любой прогноз несет на себе определенную степень ошибки, мы должны отметить очевидность возможности прогнозирования показателя лишь в среднем, таким образом возможны случайные отклонения от реального значения влево и вправо. Такие отклонения обычно предполагаются распределенными нормально, т. е. их распределения совпадают с распределением Гаусса. [c.17]
Нормальной функцией распределения, или распределением Гаусса, является интеграл этой функции, определенный для значений от минус бесконечности до х (это означает — все возможные варианты удаления события от математического ожидания) [c.70]
Теорема (неравенство) Чебышева. В сравнении с распределением Гаусса эта теорема дает очень грубое приближение. Но зато она удобна в применении, поскольку позволяет сделать это быстро, не прибегая к обращению к сложным таблицам. [c.71]
Величина а определяет вероятные границы разброса диапазона годовой доходности инвестиций Y. Предполагая, что распределение случайных величин дневных доходностей г подчиняется распределению Гаусса, можно получить формулу, связывающую вероятность реализации годовой доходности инвестиций Y, меньшую заданной величины Yv на временном горизонте, состоящем из Т периодов [c.467]
Мы отметили в гл. 2, что наиболее широко из распределений частот используется нормальное распределение, или распределение Гаусса. Отсюда вытекает то обстоятельство, что наиболее широко используемым распределением вероятностей является нормальное распределение. Это распределение непрерывное, но часто применяется при моделировании дискретных случайных переменных. [c.191]
Нормальное распределение (распределение Гаусса) представляет собой вид распределения случайных величин, с достаточной [c.136]
Для большинства финансовых операций характерно нормальное распределение вероятностей (распределение Гаусса), хотя в практике оценки риска отдельных реальных инвестиционных проектов могут использоваться и другие их виды (распределение Лапласа, распределение Стьюдента, треугольное распределение). График нормального распределения представлен на рис. 33.5. [c.162]
При установлении оптимального размера страхового запаса также учитывают разнонаправленное влияние его величины на разные элементы затрат или потерь. При уменьшении страхового запаса пропорционально сокращаются издержки его хранения, но одновременно с тем возрастает вероятность потерь и убытков, к-рые несет предприятие в случае исчерпания запаса и невозможности удовлетворить требования на данный вид ресурсов. Оптимальным считается страховой запас, при к-ром сумма этих издержек и потерь является минимальной. Для определения этого оптимума нужны расчеты по выявлению вероятности исчерпания запаса и возникновения дефицитности ресурсов (с оценкой ее размеров и длительности) и по измерению потерь или убытков, к-рые вызываются такой дефицитностью. Для выявления вероятности исчерпания запаса изучают статистич. данные за довольно длительный период времени и определяют закономерность колебаний потребления соответствующего материала и сроков выполнения заказов на пополнение запаса поставщиками. Упрощенное и достаточно надежное решение этой задачи достигается применением методики Монте-Карло, сущность к-рой заключается в имитации движения запаса на основе эмпирически установленных средних значений изучаемого показателя, показателя дисперсии (8) и таблицы случайных чисел для определенного типа распределения. Так, зная, что среднесуточное потребление данного материала а = 333 единицам, а его колеблемость 8= 64, и принимая, что распределение этих отклонений следует закону нормального распределения Гаусса, можно рассчитать сколь угодно длинный ряд суточного потребления, пользуясь таблицей случайных чисел и формулой А = а+3 Е, где Е — нормализованное отклонение по таблице случайных чисел. В табл. 1 приводятся значения суточного потребления, исчисленные по данной формуле. Аналогично строится модель вероятных сроков выполнения заказов на очередные поставки. Но при этом пользуются др. рядами случайных чисел, т. к. колебания сроков выполнения заказов лучше могут быть описаны законом распределения Пуассона. Допустим, что для данных условий ряд случайных чисел, характеризующих сроки выполнения заказов, можно записать так 6,9, 5, 5, 8, 6, 7 и т. д. Отправляясь от к.-л. исходной величины остатка материалов, от полученных расчетом рядов суточного потребления и наиболее вероятных сроков выполнения заказов, строят модель движения запаса. В табл. 2 принята нормальная партия заказа в 7500 шт., а уровень запаса, при к-ром выдается заказ на его пополнение, — 2000 шт. Чтобы эта модель давала достаточно надежную базу для выводов, ее рекомендуется продолжить условно на несколько тысяч дней, для чего обычно используют электронно-вычислительные машины. [c.270]
Нормальное распределение (распределение Гаусса) является предельным случаем почти всех реальных распределений вероятности. Поэтому оно используется в очень большом числе реальных приложений теории вероятностей. Говорят, что СВ X имеет нормальное распределение, если ее плотность вероятности имеет вид [c.23]
При обработке выборочных данных, в силу случайной природы процесса получения выборки, важно знать, каким вероятностным законам подчиняются выборочные значения исследуемого экономического показателя. Существует целый ряд распределений вероятности, которые играют роль эталона в статистических выводах. Это прежде всего равномерное распределение, нормальное распределение (распределение Гаусса) и распределение Стьюдента (/-распределение). [c.271]
Если отклонения доходности имеют случайный характер, то можно оценить вероятность реализации той или иной доходности в любом заданном интервале ее значений. Обычно для этой цели используют гауссово (или нормальное) распределение вероятностей, наиболее часто встречающееся в природе. Распределение Гаусса применяют, в частности, для оценки случайных погрешностей измерений. В пользу применения нормального распределения имеются веские основания оно всегда проявляется тогда, когда суммарная погрешность есть результат неучтенного совместного воздействия целого ряда факторов, каждый из которых дает сравнимый с другими вклад [c.201]
Наиболее известным и, наверное, наиболее распространенным в практической деятельности является нормальное распределение, иногда называемое распределением Гаусса. Данный вид распределения часто встречается в природе. Например, закону нормального распределения подчиняется случайная выборка людей по росту, весу и даже интеллектуальному развитию. Выглядит нормальное распределение как симметричная колоколообразная кривая. Среднеарифметическая ряда, подчиняющегося закону нормального распределения, равна моде и медиане этого ряда. [c.185]
Нормальное распределение (распределение Гаусса) представляет собой вид распределения случайных величин, с достаточной точностью описывающий распределение плотности вероятности результатов производственно-хозяйственной, финансовой, инновационной деятельности или изменений условий внешней среды, поскольку показатели, характеризующие их, определяются большим числом независимых случайных величин, каждая из которых в отдельности относительно других играет незначительную роль и непредсказуема. Применение нормального распределения для оценки рисков также связано с тем, что в основе данных, как правило, используется ряд дискретных значений. Эти теоретические [c.407]
Распределение нормированного отклонения выборочной средней от генеральной средней при численности выборки и —> оо определяется уравнением Лапласа-Гаусса [c.167]
Часто нормальное распределение называют распределением Гаусса, или Муавра, в честь тех, кто, как считается, открыл его — Карл Фридрих Гаусс (1777-1855) и, веком ранее, что не так достоверно, Авраам де Муавр (1667-1754). Нормальное распределение считается наиболее ценным распределением, благодаря тому, что точно моделирует многие явления. Давайте рассмотрим приспособление, более известное как доска Галтона (рисунок 3-5). Это вертикально установленная доска в форме равнобедренного треугольника. В доске расположены колышки, один в верхнем ряду, два во втором, и так далее. Каждый последующий ряд имеет на один колышек больше. Колышки в сечении треугольные, так что, когда падает шарик, у него есть вероятность 50/50 пойти вправо или влево. В основании доски находится серия желобов для подсчета попаданий каждого броска. [c.89]
Концепция случайных блужданий проста, но богата своими приложениями не только в финансах, но и в физике, и в описании естественных процессов. Бесспорно, это одна из наиболее важных фундаментальных концепций, как в современной физике, так и в современных финансах, как являющаяся основанием теории элементарных частиц, представляющих собой строительные блоки Вселенной, так и описывающая сложные процессы вокруг нас. В простейшей вы бросаете монету, в результате чего двигаетесь вверх, если выпал "орел" или вниз -если выпала "решка". Где вы окажетесь после множественного повторения таких подбрасываний Ответ на поставленный вопрос многозначен в среднем вы остаетесь в той же самой позиции, так как среднее от одного шага вверх и одного шага вниз эквивалентно отсутствию какого-либо движения. Однако, ясно, что существуют флуктуации вокруг этого нулевого среднего значения, которые увеличиваются с увеличением числа подбрасываний. На Рис. 19 представлена траектория синтетически случайной рыночной цены, смоделированная компьютером, для определения конечного ценового сдвига в результате многократного изменения "цен". В данном случае, шаг или приращение имеет случайный "знак", а амплитуды приращений последовательных распределены согласно так называемому закону распределения Гаусса, графически изображаемого в виде хорошо известной колоколообразной кривой. [c.51]
| Рис. 19. Синтетически случайная рыночная цена (или позиции случайного блуждания полученная бросанием "компьютерной монеты" для определения направления изменени цены вверх или вниз. В этой модели шаг или интервал приращения имеет случайный знак амплитуду, распределенную согласно, так называемому распределению Гаусса с 11 стандартным отклонением. Те же самые приращения использованы при построении Рис. К синтетическая траектория, построенная здесь, таким образом, есть не что иное, ка нарастающая сумма приращений, представленных на Рис. 16. | 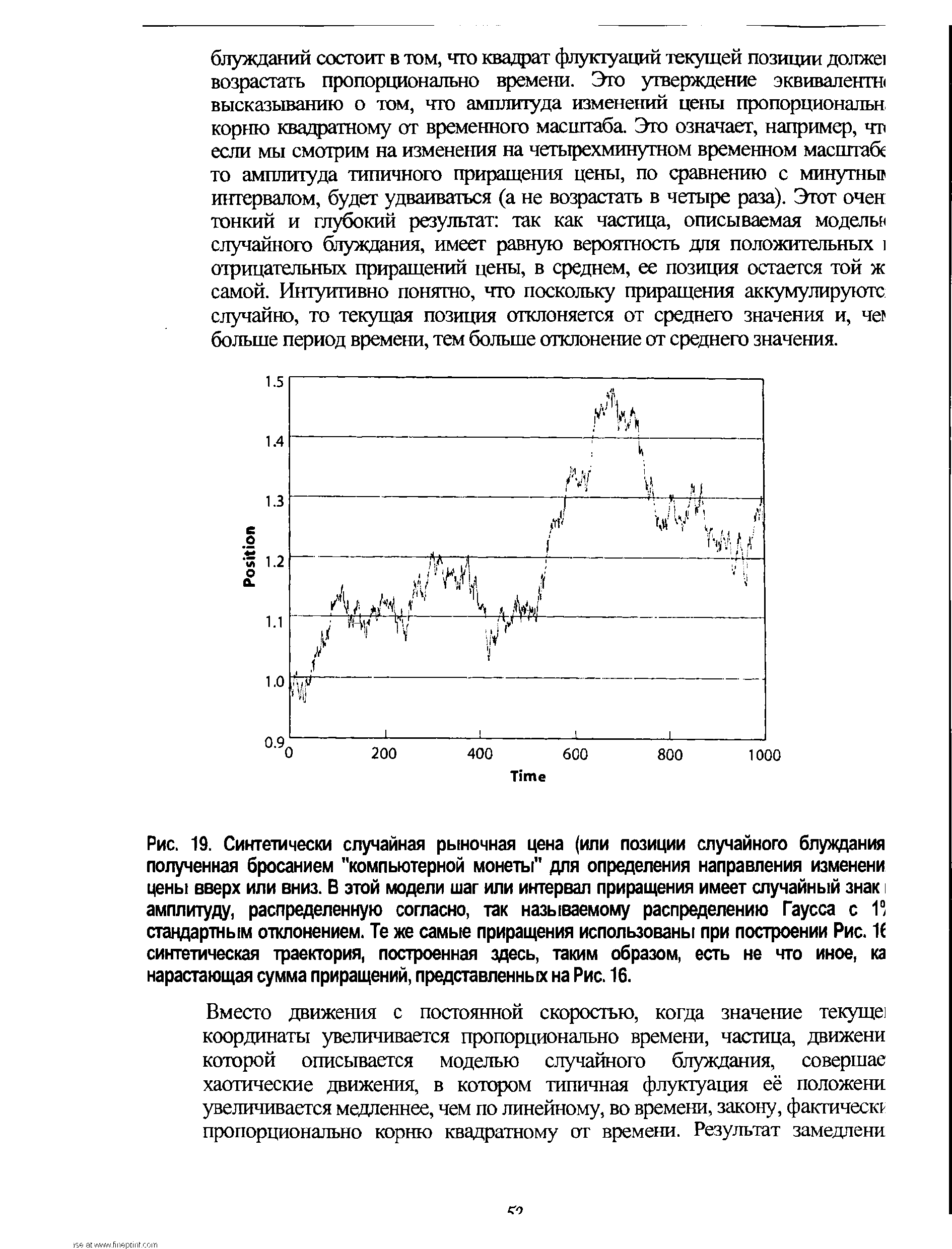 |
Значение функции принадлежности ЦА(Щ) определяется экспертом или руководителем. У каждого специалиста эта функция может иметь различный вид. Один человек может считать, что высокий рост начинается с -1.6 м, а другой считает, что сейчас время акселератов и поэтому высокий рост начинается с 1,7 м. И сам вид функции VAfaJ, описывающей один и тот же объект, разные люди могут формировать по-разному. Один считает, что для данного объекта она симметрична и имеет вид равнобедренного треугольника, другой -что это равнобедренная трапеция, а третий - что она имеет вид фигуры неправильной формы. В этом принципиальное отличие функции /2A(Uj) от функции распределения в теории вероятностей. Сотнями экспериментов установлено, что рассеивание снарядов артиллерийских орудий подчиняется закону распределения Гаусса. И ни один специалист не имеет права считать, что оно подчиняется какому-нибудь другому закону распределения, например Пуассона. Если он так считает, он должен это доказать. Т.е. функция JUA(UJ) - это функция, определяющая субъективное мнение специалиста, а скажем, функция распределения случайной величины или закон Байеса - это выражение объективной закономерности, независимой от отношения специалиста к этой закономерности. [c.92]
Используя R/S-анализ для поддержки гипотезы фрактального рынка, я показываю модели, объясняющие полученные результаты. Часть 4 рассматривает деятельность рынка с точки зрения стохастических процессов по существу, в ней разбирается фрактальный шум. В Главе 13, на основе использования R/S-анализа, различные "цветные" шумы анализируются и сравниваются с анализом рынка. Полученные результаты удивительно похожи. Кроме того, дается значимое объяснение поведению волатильности. В Главе 14 обсуждается статистика процессов фрактального шума, которые выдвигаются в качестве альтернативы традиционному нормальному распределению (распределению Гаусса). Обсуждается влияние фрактальных распределений на модели рынка. В Главе 15 показано влияние фрактальной статистики на проблему выбора портфеля и опционное ценообразование. Рассматриваются методы адаптирования таких моделей к фрактальным распределениям. [c.7]
Устойчивый паретиан или фрактальная гипотеза. Теория, утверждающая, что в характеристической функции семейства фрактальных распределений величина характеристического показателя альфа может варьироваться между 1 и 2. См. альфа , фрактальное распределение , гауссиана . [c.290]
