Оператор 25. Подпрограмма определения плотности вероятности теоретического распределения для каждого интервала группировки. Выборка может быть произведена из таблиц, приведенных в [20]. [c.77]
Как легко понять, функция F(r ) должна изменяться от нуля до единицы и не убывать с ростом ч. Если функция F(r)) достаточно гладкая, то вместо нее можно использовать функцию плотности вероятностей /(т)), связанную с F(-n) соотношением [c.153]
Функция плотности вероятностей в каждой точке т] имеет следующий смысл вероятность того, что величина у примет значение из интервала (ц, f +dt ), приблизительно равна f(i )dr. Функция Р(ц) (или /(т))) содержит всю имеющуюся информацию о величине у, которая в данном случае называется случайной величиной. Можно, например, подсчитать среднее значение величины у . [c.153]
Закон нормального распределения, как известно, характеризуется плотностью вероятностей, которая определяется как [c.59]
Под зависимостью вероятности р от цены х будем понимать тот факт, что в данный момент времени цена на товар будет не больше х. Иногда удобнее работать не с вероятностью некоторого события, а с плотностью вероятностей этого события. [c.451]
Отсюда вытекает связь между вероятностью и плотностью вероятностей [c.452]
Графически связь между плотностью вероятностей и вероятностью проиллюстрирована на рис. 17.2. В качестве примера взят нормальный закон распределения с параметрами среднее значение равно 2,4, дисперсия — 0,8. [c.452]
Постановку задачи, определения ситуации на рынке товаров и услуг рассмотрим на примере одного продукта. Поскольку эволюция экономической системы представляет собой сочетание двух процессов — один детерминированный, обусловленный объективными причинами, действующими в данной экономической системе, а второй — вероятностный, то для ее описания применяют уравнение Колмогорова, отображающее изменение плотности вероятности в различные моменты времени [c.452]
| Рис. 17.2. Распределение плотности вероятностей для нормального закона (1) и вероятности (2) в зависимости от цены х | 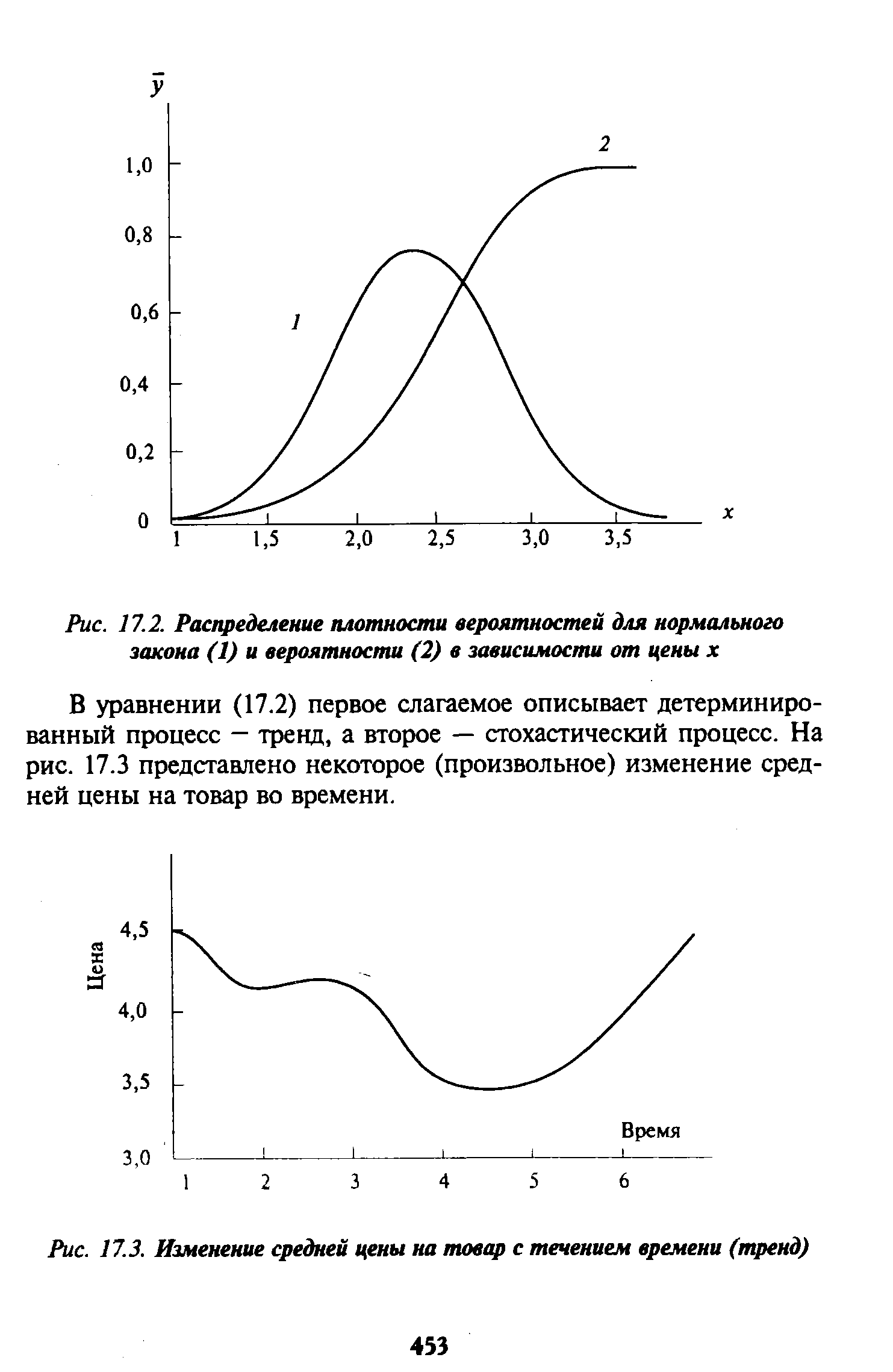 |
На рис. 17.4 представлено распределение плотности вероятностей для некоторого момента времени в зависимости от цены на товар. [c.454]
Изменение распределения плотности вероятностей в зависимости от условной цены, начиная для некоторого момента времени, представлено на рис. 17.5. Из зависимости между плотностью вероятностей и вероятностью (17.1) вытекает, что для одной и той же цены вероятность будет различной в разные моменты времени. [c.454]
| Рис. 17.4. Зависимость плотности вероятностей от цены на товар в некоторый момент времени | 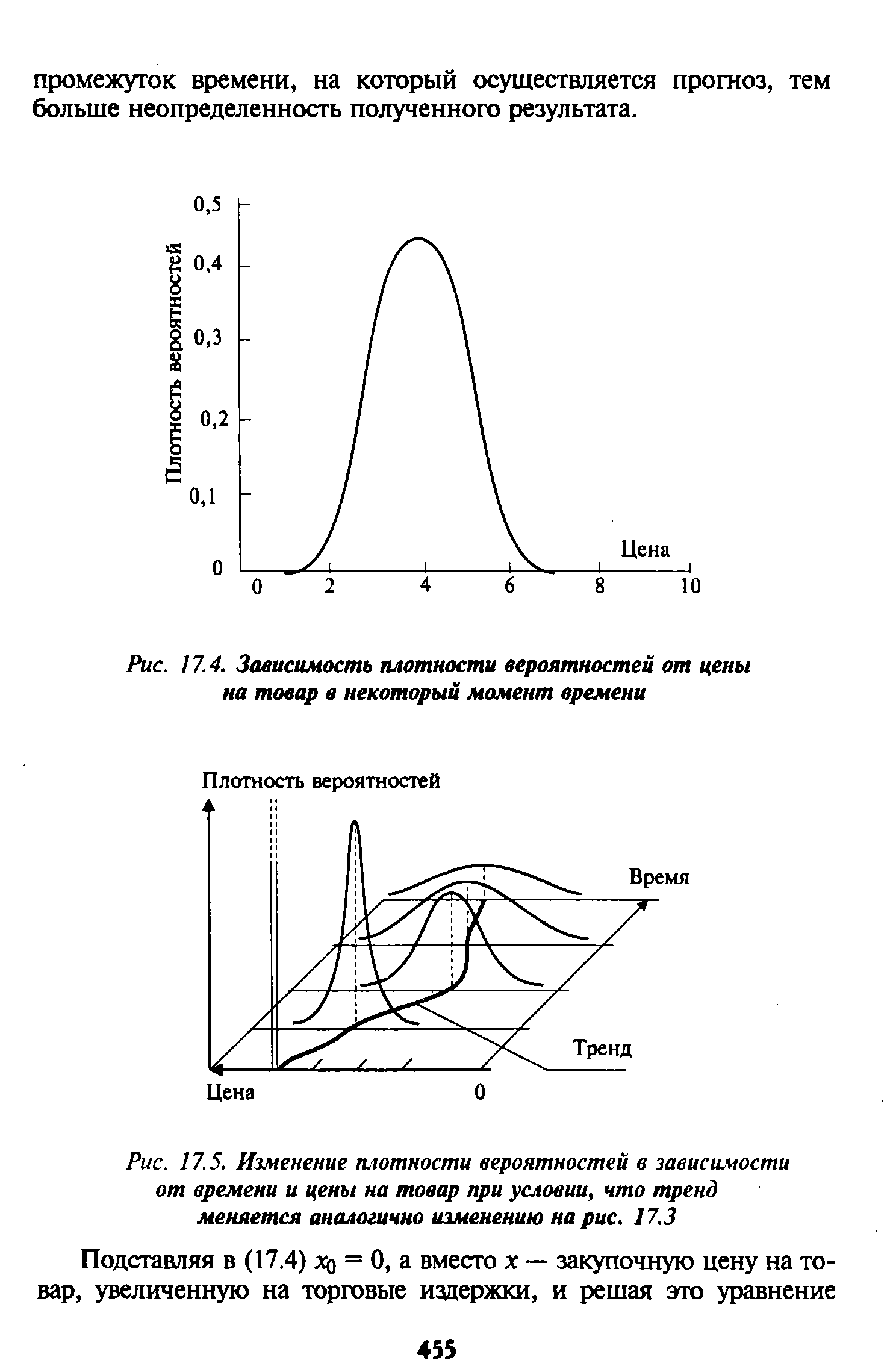 |
Вероятностные модели прогнозирования рыночной ситуации учитывают случайную составляющую развития экономической системы. Для описания стохастической системы применяется уравнение Колмогорова, его решение представляет собой распределение плотности вероятностей. Причем чем более длительный промежуток времени выбирается для прогноза, тем больше дисперсия распределения вероятностей и тем больше неопределенность полученного результата. Однако оценка риска прогнозируемой ситуации на рынке на основе изученных методов обеспечивает предпринимателя информацией о возможных (вероятных) потерях и позволяет принять меры по их снижению. [c.459]
После предварительной обработки статистического материала была принята гипотеза о нормальном законе распределения показателей фактической надежности, т.е. плотность вероятности [c.233]
Непрерывная случайная величина может принимать все возможные значения и задаваться в виде функции плотности вероятности. Одним из наиболее простых примеров служит величина, равномерно распределенная по некоторому интервалу, т.е. принимающая все значения из этого интервала с равной вероятностью и не принимающая значений вне этого интервала. [c.262]
Плотность вероятности такой величины равна [c.262]
В формуле для определения математического ожидания непрерывной случайной величины вместо вероятности используется функция плотности вероятности [c.263]
Плотностью вероятности (плотностью распределения или просто плотностью) ф(х) непрерывной случайной величины X называется производная ее функции распределения [c.30]
Плотность вероятности <р(х), как и функция распределения [c.31]
График плотности вероятности называется кривой распределения. [c.31]
Пример 2.7. По данным примера 2.6 найти плотность вероятности случайной величины X. [c.31]
Решение. Плотность вероятности q> (x) = F (x т. е. [c.31]
Свойства плотности вероятности непрерывной случайной величины [c.31]
Плотность вероятности — неотрицательная функция, т.е. <р(х)>0. [c.31]
Вероятность попадания непрерывной случайной величины в интервал [a,b] равна определенному интегралу от ее плотности вероятности в пределах от а до Ъ (см. рис. 2.2), т.е. [c.31]
Функция распределения непрерывной случайной величины (см. рис. 2.3) может быть выражена через плотность вероятности по формуле [c.31]
Несобственный интеграл в бесконечных пределах от плотности вероятности непрерывной случайной величины равен единице [c.32]
Геометрически свойства 1 и 4 плотности вероятности означают, что ее график — кривая распределения — лежит не ниже оси абсцисс, и полная площадь фигуры, ограниченной кривой распределения и осью абсцисс, равна единице. [c.32]
Непрерывная случайная величина X имеет равномерный закон распределения на отрезке [а, Ь], если ее плотность вероятности постоянна на этом отрезке и равна нулю вне его, т.е. [c.34]
Непрерывная случайная величина X имеет показательный (экспоненциальный) закон распределения с параметром Я,, если ее плотность вероятности имеет вид [c.34]
Плотностью вероятности (плотностью распределения или совместной плотностью) непрерывной двумерной случайной величины (X,Y) называется вторая смешанная частная производная ее функции распределения, т.е. [c.37]
Свойства плотности вероятности двумерной случайной величины q>(x, у) аналогичны свойствам плотности вероятности одномерной случайной величины [c.37]
Условные плотности вероятности <ру(х) и ух(у) двумерной случайной величины (X, Y) определяются по формулам [c.37]
Числовые характеристики условных распределений условные математические ожидания Мх( Y) и Му(Х) и условные дисперсии DX(Y) и Dy(X). Эти характеристики находятся по обычным формулам математического ожидания и дисперсии, в которых вместо вероятностей событий или плотностей вероятности используются условные вероятности или условные плотности вероятности. [c.38]
Плотность вероятностей распределения Стыодента описывается функцией [c.191]
Асимметрия служит для оценки симметричности распределения случайной величины относительно средней. Если асимметрия — положительное число, распределение имеет сдвиг в сторону положительных значений, иначе — в сторону отрицательных значений. Эксцесс является характеристикой остроконечности или сглаженности кривой распределения плотности вероятности случайной величины. Эксцесс равен нулю для нормального распределения, положителен для остроконечных и отрицателен для сглаженных по сравнению с нормальной плотностью распределения. [c.462]
Смотреть страницы где упоминается термин Плотность вероятности
: [c.81] [c.154] [c.392] [c.59] [c.167] [c.452] [c.452] [c.454] [c.455] [c.263] [c.276]Вводный курс эконометрики (2000) -- [ c.19 , c.34 ]
