Построение на факторном пространстве векторов ковариационной матрицы (рис. 4.9) позволило отобрать и объединить значимые факторы в следующие группы [c.216]
| Рис. 4.9. Положение собственных векторов ковариационной матрицы, | 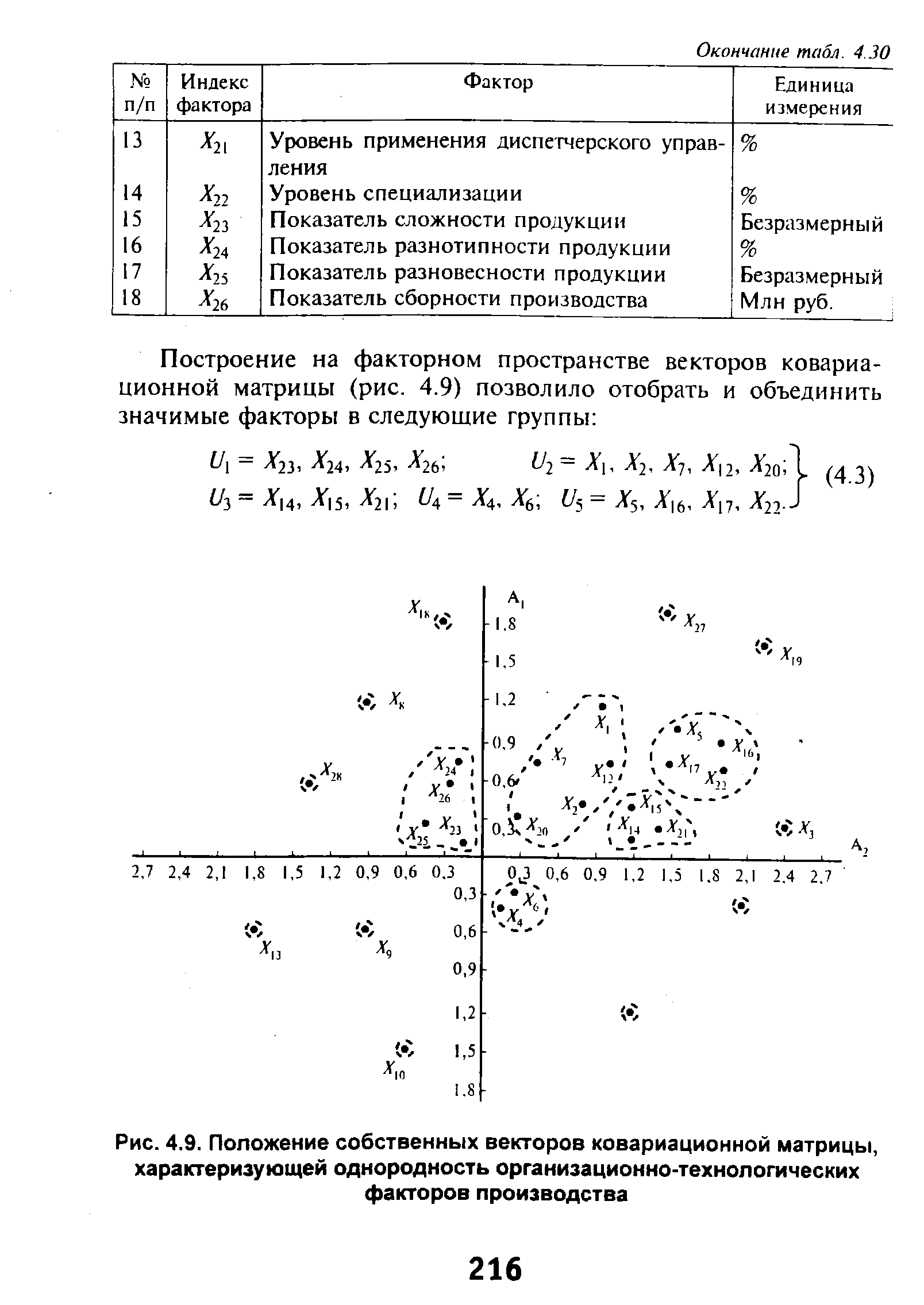 |
Ковариационная матрица и ее определитель, называемый обобщенной дисперсией n-мерной случайной величины, являются аналогами дисперсии одномерной случайной величины и характеризуют степень случайного разброса отдельно по каждой составляющей и в целом по и-мерной величине. [c.41]
Ковариационная матрица и ее выборочная оценка [c.91]
Рассматривая ковариационную матрицу Y , легко заме- [c.92]
В сокращенном виде ковариационная матрица вектора оценок параметров У t имеет вид [c.92]
Теперь с помощью преобразований, аналогичных проведенным при получении формул (4.15), (4.16), найдем, что ковариационная матрица вектора оценок Ь, т. е. [c.94]
Матрица СС также, как и ковариационные матрицы V, и У . является [c.95]
В то же время вектор оценок b и его ковариационная матрица У t в соответствии с формулами (4.8) и (4.16) пропорциональны [c.109]
При моделировании реальных экономических процессов мы нередко сталкиваемся с ситуациями, в которых условия классической линейной модели регрессии оказываются нарушенными. В частности, могут не выполняться предпосылки 3 и 4 регрессионного анализа (см. (3.24) и (3.25)) о том, что случайные возмущения (ошибки) модели имеют постоянную дисперсию и не коррелированы между собой. Для линейной множественной модели эти предпосылки означают (см. 4.2), что ковариационная матрица вектора возмущений (ошибок) е имеет вид [c.150]
Сравнивая обобщенную модель с классической ( 4.2), видим, что она отличается от классической только видом ковариационной матрицы вместо ]Г Е= а2Е для [c.151]
Однако полученная ранее формула для ковариационной матрицы вектора оценок оказывается неприемлемой в условиях [c.151]
Следовательно, если в качестве оценки ковариационной матрицы У t в соотношении (7.3) заменить а2 на s2, т. е. взять [c.152]
В заключение отметим, что для применения обобщенного метода наименьших квадратов необходимо знание ковариационной матрицы вектора возмущений Q, что встречается крайне редко в практике эконометрического моделирования. Если же считать все я(л+1)/2 элементов симметричной ковариационной матрицы Q неизвестными параметрами обобщенной модели (в дополнении к (р+l) параметрам (3/), то общее число параметров значительно превысит число наблюдений я, что сделает оценку этих параметров неразрешимой задачей. Поэтому для практической реализации обобщенного метода наименьших квадратов необходимо вводить дополнительные условия на структуру матрицы Q. Так мы приходим к практически реализуемому (или доступному) обобщенному методу наименьших квадратов, рассматриваемому в 7.11. [c.155]
В самом деле, при построении t- и / -статистик, которые служат инструментом для проверки (тестирования) гипотез, существенное значение имеют оценки дисперсий и ковариаций параметров р, (/= 1,..., и), т. е. ковариационная матрица 6. Между [c.157]
Однако, даже если с помощью взвешенного метода наименьших квадратов не удается устранить гетероскедастичность, ковариационная матрица ь оценок параметров регрессии (3 [c.167]
Учитывая (7.37), (7.38), ковариационную матрицу вектора возмущений е для модели с автокорреляционными остатками можно представить в виде [c.183]
Приведем теперь (опуская промежуточные вычисления) формулы для вычисления ковариационных матриц оценок b, b , g. [c.245]
При равенстве ковариационных матриц классов / и / [c.204]
Следует отметить некоторые интересные свойства ковариационной матрицы. Во-первых, матрица является квадратной, т.е. количество столбцов равняется количеству строк, а общее число ячеек для N ценных бумаг равняется N2. [c.185]
Вычислите стандартное отклонение портфеля по заданной ковариационной матрице для трех ценных бумаг и процентному содержанию бумаг в портфеле. [c.189]
Ниже, в 4.3, рассматривается ковариационная матрица вектора возмущений ]Г , являющаяся многомерным аналогом дисперсии одной переменной. Поэтому в новых терминах1 приведенные ранее (с. 61, 82 и здесь) предпосылки для множественного регрессионного анализа могут быть записаны следующим образом 2 [c.86]
МатрицаА/(ее ) представляет собой ковариационную матрицу вектора возмущений [c.93]
Будем считать, что модель (7.25) гетероскедастич-н а, т. е. дисперсии возмущений (ошибок) ст (/ = ,...,п) не равны между собой, и сами возмущения е/ и е (k = 1,..., я) не кор-релированы. Это означает, что ковариационная матрица вектора возмущений ХЕ = —диагональная [c.163]
Очевидно, дисперсия D(v,)=l, т. е. модель (7.27) гомоскедас-тична. При этом ковариационная матрица Z<= становится единичной, а сама модель (7.27) — классической. [c.164]
Применение формулы (7.28) для отыскания параметра р, т. е. обобщенный метод наименьших квадратов для модели с гете-роскедасттностъю, когда ковариационная матрица возмущений ZE= есть диагональная матрица (7.26), называется взвешенным методом наименьших квадратов. [c.164]
Затем найдем линейное преобразование, д наго нал изующее ковариационную матрицу. Соответствующая матрица составлена из столбцов - собственных векторов ковариационной матрицы [c.133]
Элемент, находящийся в ячейке (/, у), обозначает ковариацию между ценными бумагами / и/. Например, элемент в ячейке (1,3) обозначает ковариацию между первой и третьей ценными бумагами, которая в данном случае равна 145. Элемент в ячейке (/, /) обозначает дисперсию /-ой ценной бумаги. Например, дисперсия второй ценной бумаги находится в ячейке (2,2) и равняется 854. Стандартное отклонение любого портфеля, состоящего из инвестиций в акции компаний Able, Baker и harlie, может быть вычислено с помощью ковариационной матрицы и формулы, приведенной в уравнении (7.66). [c.184]
Любой ковариационной матрице соответствует корреляционная матрица, которая может быть определена по данным ковариационной матрицы и уравнению (7.5). С помощью данного уравнения можно показать, что корреляция между двумя ценными бумагами /и/равняется о,../о,о.. Значения а, а и а могут быть получены из ковариационной матрицы. Например, г.. = 187/(Vl46x V854) = = 0,53, [c.193]
Хотя данный алгоритм и выходит за рамки данной книги, необходимо понимать, как он работает. Для начала инвестор должен оценить вектор ожидаемых доходностей и ковариационную матрицу. Например, рассмотрим портфель из трех акций, представленный ранее в данной главе14. Проведем оценку вектора ожидаемых доходностей, обозначенного как ER, и ковариационной матрицы, обозначенной как УС [c.221]
Смотреть страницы где упоминается термин Ковариационная матрица
: [c.92] [c.93] [c.152] [c.152] [c.157] [c.157] [c.185] [c.197] [c.237] [c.300] [c.204] [c.172] [c.51] [c.133] [c.184] [c.184] [c.189] [c.193]Матричное дифференциальное исчисление с приложениями к статистике и эконометрике (2002) -- [ c.310 , c.311 ]
Эконометрика начальный курс (2004) -- [ c.514 ]
