| Рис. 4.9. Положение собственных векторов ковариационной матрицы, | 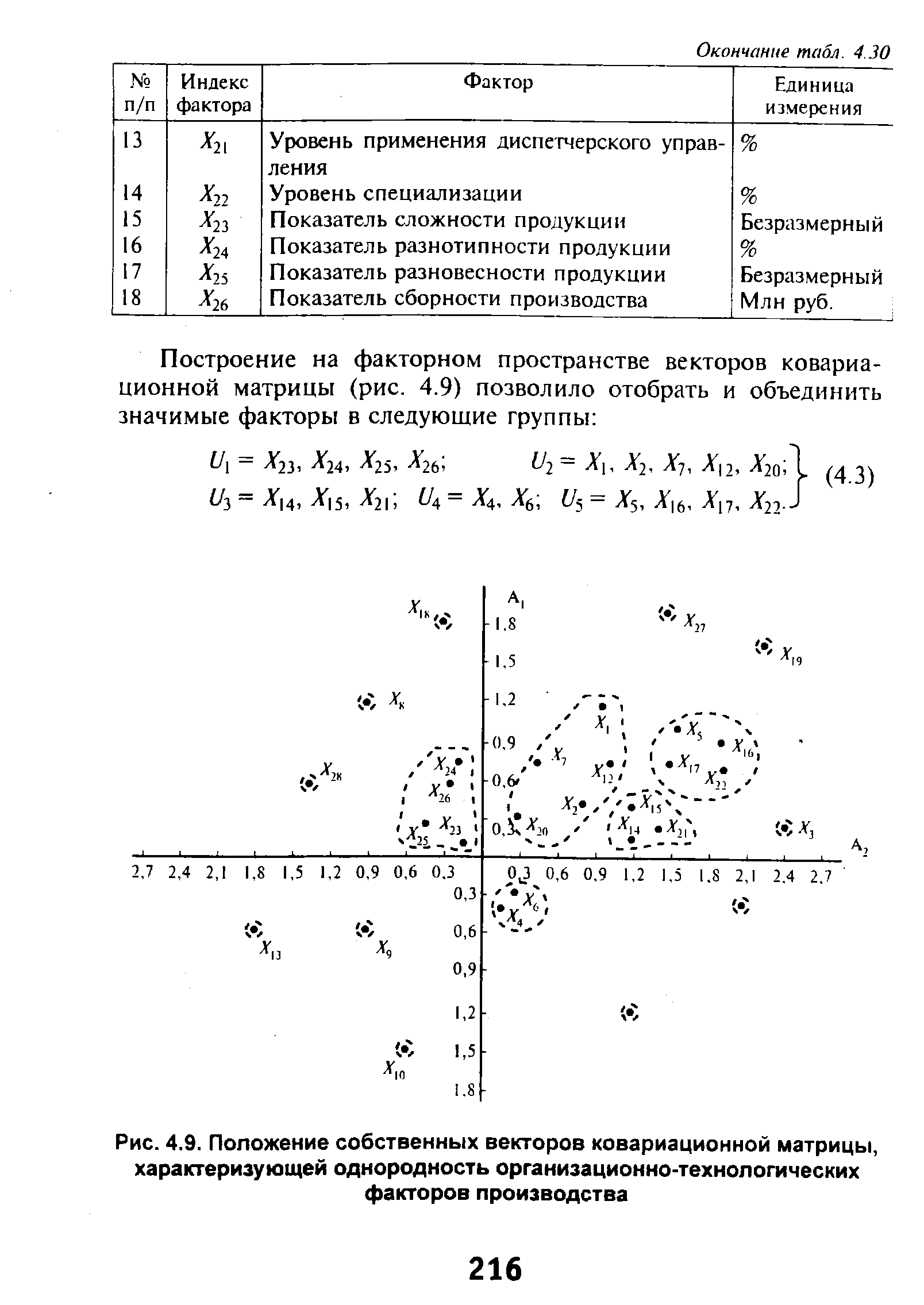 |
Вектор с 0 называется собственным вектором квадратной [c.271]
Собственный вектор х определен с точностью до коэффициента пропорциональности. [c.271]
Найти собственные значения и собственные векторы матрицы [c.272]
Разным собственным значениям матрицы соответствуют линейно независимые собственные векторы. [c.272]
Так как собственные векторы известны, по формуле (7.29) можно определить главные компоненты. При этом обычно довольствуются меньшим, чем л, числом главных компонент, но достаточным, чтобы воспроизвести большую часть дисперсии. По мере выделения главных компонент доля общей дисперсии становится все меньше и меньше. Процедуру вычисления главных компонент прекращают в тот момент, когда собственные значения, соответствующие каждый раз наибольшим дисперсиям, становятся пренебрежимо малыми. Количество выделенных главных компонент г в общем случае значительно меньше числа объясняющих переменных т. По г главным компонентам строится матрица Z. С помощью главных компонент оцениваются параметры регрессии [c.317]
Используя иерархический синтез для взвешивания собственных векторов матриц весами критериев, вычисляется сумма по всем соответствующим взвешенным компонентам собственных векторов матриц целей уровня иерархии, лежащего ниже. [c.98]
Вычисление главного собственного вектора примитивных матриц [c.23]
Собственный вектор А, соответствующий собственному значению 2 , , [c.25]
Вычислять вектор приоритета (собственный вектор) для каждой мат- [c.61]
Urn -г.—JT = w, A = e A e, где с - постоянная, aw- собственный вектор, [c.73]
Оценка метода собственного вектора в ряду методов построения [c.94]
Собственные векторы неотрицательных матриц [c.262]
Среди собственных векторов, принадлежащих ХА, имеется неотрицательный вектор. [c.262]
Затем найдем линейное преобразование, д наго нал изующее ковариационную матрицу. Соответствующая матрица составлена из столбцов - собственных векторов ковариационной матрицы [c.133]
Собственные векторы оказываются связанными с полино- [c.277]
В случае А > О все неотрицательные собственные векторы матрицы А положительны и принадлежат только ее максимальному по модулю сйбственному значению ХА. Кроме того, в этом случае любые два положительных собственных вектора х и У отличаются лишь числовым множителем у = ССх. [c.262]
Смотреть страницы где упоминается термин Собственный вектор
: [c.272] [c.272] [c.305] [c.317] [c.317] [c.24] [c.24] [c.25] [c.25] [c.25] [c.25] [c.25] [c.26] [c.26] [c.57] [c.57] [c.68] [c.72] [c.76] [c.79] [c.79] [c.80] [c.101] [c.101] [c.103] [c.110] [c.124] [c.277]Эконометрика начальный курс (2004) -- [ c.496 ]
