Где каждое B(ijt) представляет собой фактор, выраженный в терминах корреляционного коэффициента (t, t) и, обычно, называется коэффициентом (i,t) инверсной корреляционной матрицы. Формула (1) выражает тот факт, что каждое прошлое изменение г,- влияет на будущее изменение г, пропорционально величине этого изменения и коэффициенту B(i,t)/B(t,t), который не равен нулю только, если существует ненулевая корреляция между моментами времени int. С помощью формулы (1) мы получаем наилучший линейный прогноз, в том смысле, что мы можем минимизировать ошибку в предсказании (минимизация вариации). Принимая на вооружение эту линейную модель, можно получить мощную торговую стратегию покупать, если mt > 0 (ожидаемый рост будущих цен) и продавая, если /я, < О (ожидаемое падение будущих цен). [c.50]
Формальное содержание этого подхода заключается в гипотезе о полностью специфицированной линейной рекурсивной причинной модели, оценке ее параметров, а затем использовании этих значений для воспроизведения эмпирической корреляционной матрицы. Основная идея процедуры — это положение о том, что модель, которая не воспроизводит эмпирических корреляций, должна быть отвергнута. [c.222]
Второй ситуацией является случай с неизвестным каузальным приоритетом среди переменных. Допустим, что мы имеем набор переменных, для которых не известен каузальный порядок причина-следствие, и имеются две гипотезы, каждая по-своему устанавливающая его, постулируя отсутствие тех или иных возможных отношений. Описываемый подход может быть применен как для сравнения этих теорий, так и для их отбрасывания. Заметим, что в процедуре сравнения одна модель-гипотеза может оказаться лучше другой, но никогда — правильной. Более того, если одна из гипотез близка к тому, чтобы описываться полной рекурсивной системой, то обычно она работает, лучше воспроизводя корреляционную матрицу, и, естественно, будет выбираться как более удачная, даже если она весьма далека от истины. [c.223]
Корреляционная матрица активов, построенная как точечная оценка за два [c.101]
| Таблица 7.4. Корреляционная матрица российских фондовых активов |  |
| Рис. 7.6. Корреляционная матрица приоритизации | 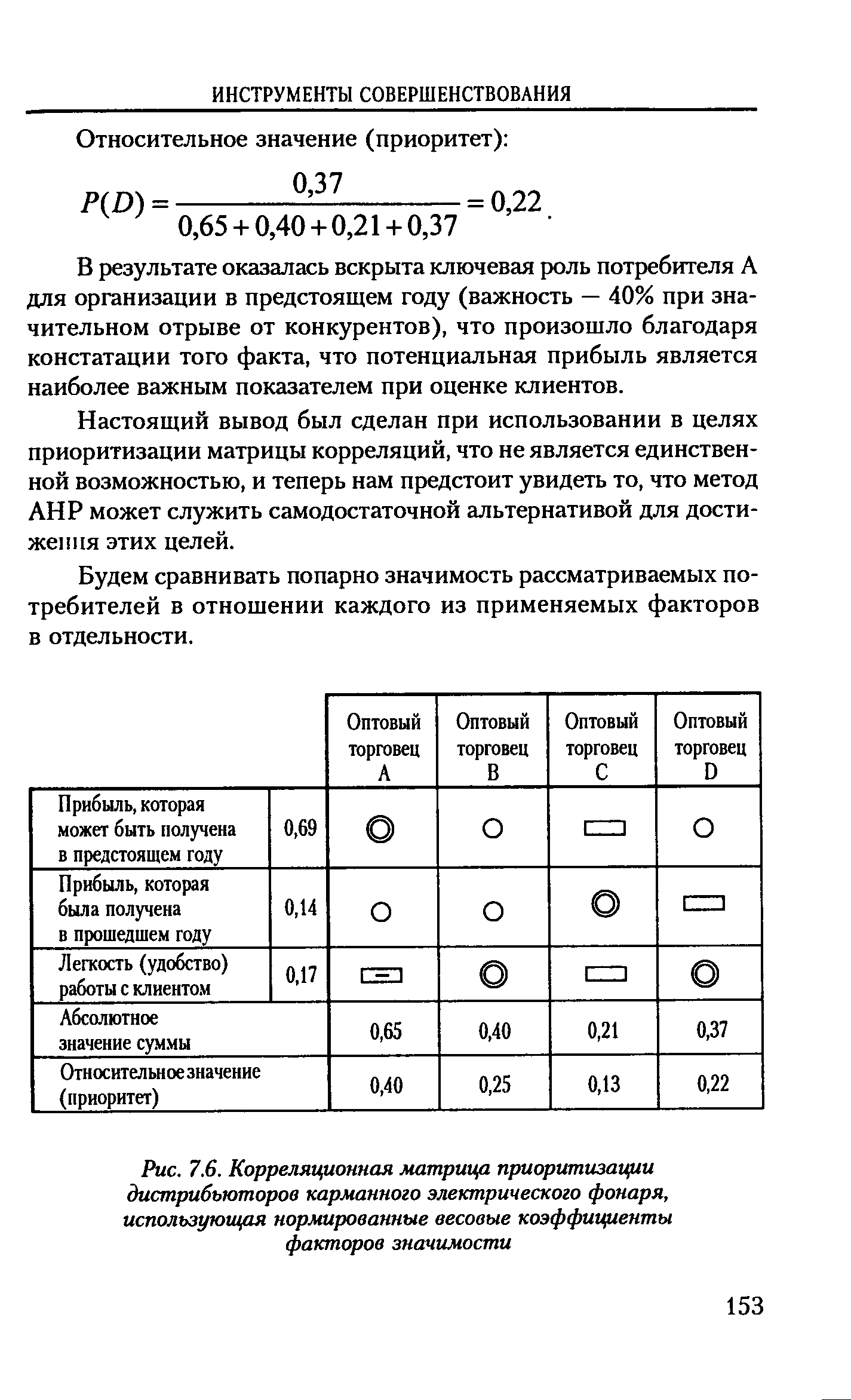 |
| Рис. 8.4. Корреляционная матрица, используемая | 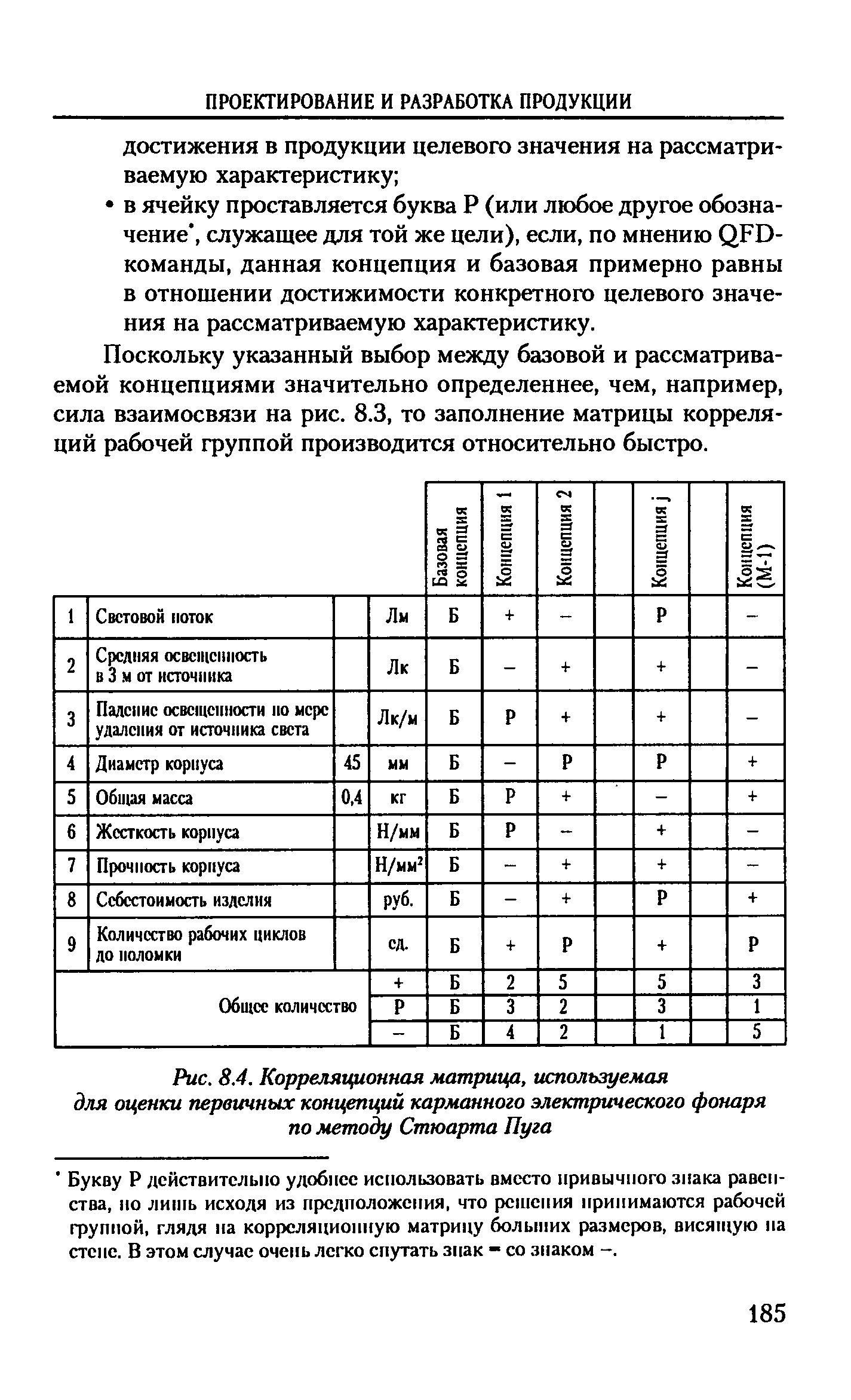 |
Корреляционная матрица, позволяющая оптимизировать значе- [c.196]
Примененные вместе, корреляционные матрицы позволят [c.221]
Составляем корреляционную матрицу [c.118]
Величину звездного плеча а (табл. 4.19) выбирают из условия равенства нулю недиагонального члена корреляционной матрицы [c.183]
Факторы Корреляционная матрица признаков [c.493]
Любой ковариационной матрице соответствует корреляционная матрица, которая может быть определена по данным ковариационной матрицы и уравнению (7.5). С помощью данного уравнения можно показать, что корреляция между двумя ценными бумагами /и/равняется о,../о,о.. Значения а, а и а могут быть получены из ковариационной матрицы. Например, г.. = 187/(Vl46x V854) = = 0,53, [c.193]
Следует также проверить, скоррелированны ли действия скрытых элементов. В многомерном регрессионном анализе при росте муль-тиколлинеарности значения коэффициентов регрессии становятся все менее надежными. Так же и здесь предпочтительно, чтобы выходы скрытых элементов одного слоя были некоррелированны. Нужно найти собственные значения корреляционной матрицы для выходов скрытых узлов по данным обработки всех обучающих примеров. При полной некоррелированности все собственные значения будут равны единице, а отличия от единицы говорят об избыточном числе скрытых элементов. Кроме того, для анализа внутреннего представления нейронно-сетевой модели часто применяются методы кластерного анализа (см. [ 127]). [c.64]
Коинтеграция временных рядов 282-285, 334-335 Коллинеарность факторов 92 Конфлюэнтный анализ 17 Коррелограмма 23 3 Корреляционная матрица 112 Корреляция 10, 12, 14, 20 Коэффициент [c.338]
Вычислим в Ex el коэффициент корреляции. Для этого выбираем Сервис / Анализ данных / Корреляция и после заполнения диалогового окна получаем корреляционную матрицу [c.18]
