Как легко понять, функция F(r ) должна изменяться от нуля до единицы и не убывать с ростом ч. Если функция F(r)) достаточно гладкая, то вместо нее можно использовать функцию плотности вероятностей /(т)), связанную с F(-n) соотношением [c.153]
Функция плотности вероятностей в каждой точке т] имеет следующий смысл вероятность того, что величина у примет значение из интервала (ц, f +dt ), приблизительно равна f(i )dr. Функция Р(ц) (или /(т))) содержит всю имеющуюся информацию о величине у, которая в данном случае называется случайной величиной. Можно, например, подсчитать среднее значение величины у . [c.153]
Как уже отмечалось, часто пользуются типом распределения, которое называется нормальным. Формула функции плотности нормального распределения [c.197]
Непрерывная случайная величина может принимать все возможные значения и задаваться в виде функции плотности вероятности. Одним из наиболее простых примеров служит величина, равномерно распределенная по некоторому интервалу, т.е. принимающая все значения из этого интервала с равной вероятностью и не принимающая значений вне этого интервала. [c.262]
В формуле для определения математического ожидания непрерывной случайной величины вместо вероятности используется функция плотности вероятности [c.263]
Несмотря на то, что метод Монте-Карло обладает радом достоинств, он не распространен и широко не используется в бизнесе, причина этого — неопределенность функций плотности переменных, используемых при подсчете потоков наличности. Другая проблема та же, что и при использовании метода сценариев — применение обоих методов не дает однозначного ответа на вопрос о необходимости реализации данного проекта. [c.252]
Полученное выражение позволяет сделать вывод о том, что площадь, ограниченная некоторыми двумя значениями величины F — F, и F2 вследствие конструкции функции плотности Ь,х> показывает вероятность достижения величины результата F в пределах (F,, F2), и что фактические значения (Рф) могут отклоняться в любом направлении вследствие случайных воздействий от расчетного во время составления планируемого значения (F ). [c.195]
Функция плотности вероятности (4.38) оказывается представленной в виде произведения двух функций [c.128]
Первая из них не зависит от параметров j и м/. а вторая зависит от параметров , - и ДУ и является функцией от в,- и bj, r. е. функция плотности вероятности (4.38) удовлетворяет критерию факторизации Неймана - Фишера, что и доказывает достаточность статистики (а, Ь) [c.128]
Пример. Функция плотности закона равной вероятности имеет вид (рис. 2) [c.20]
| Рис. 2. Функция плотности закона равной вероятности. | 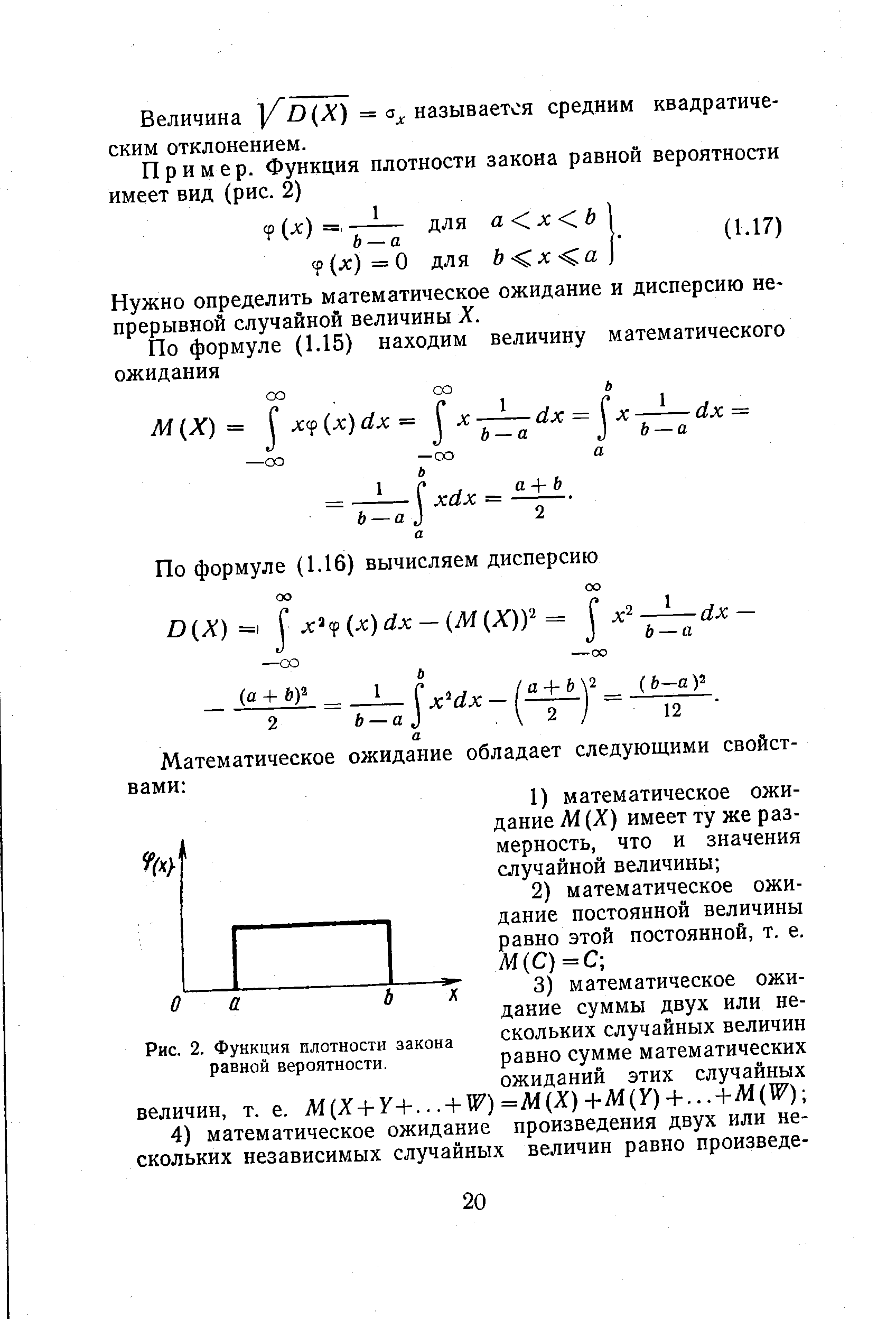 |
| Рис. 4. Функция плотности нормального закона. | 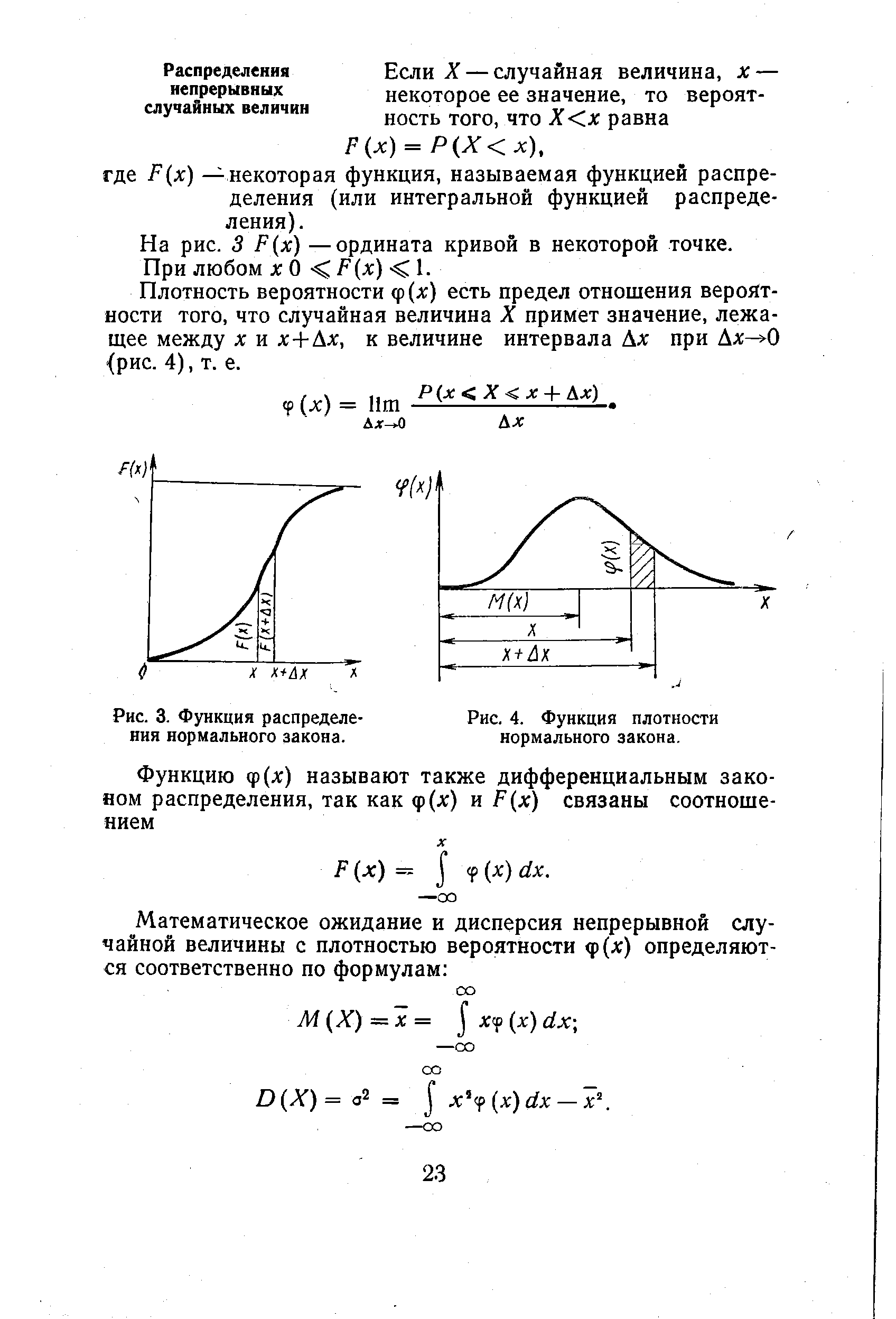 |
Функции плотности (рис. 5) и функции распределения экспоненциального закона имеют вид [c.24]
| Рис. 5. Функция плотности экспоненциального закона. | 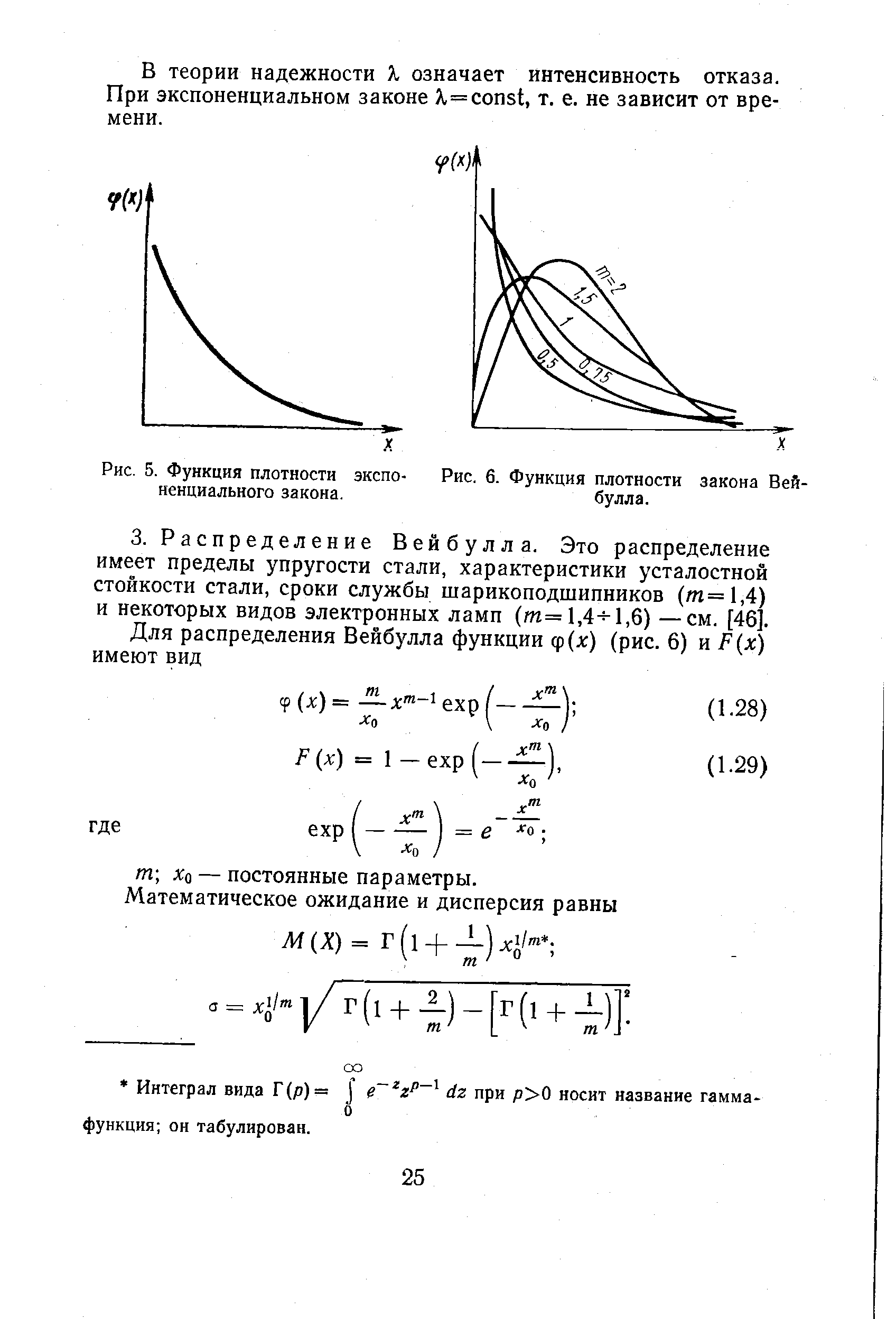 |
| Рис. 6. Функция плотности закона Вей-булла. | 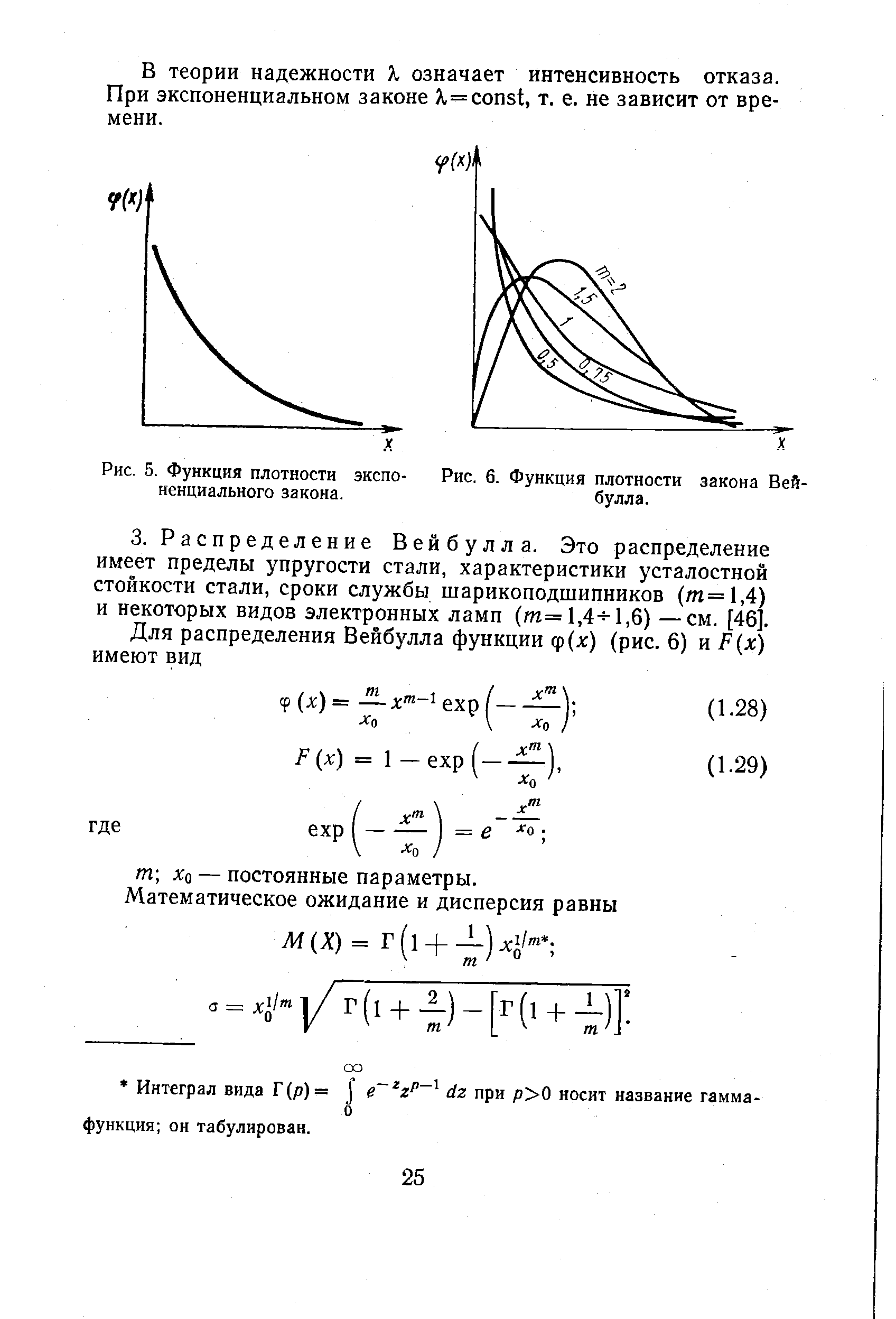 |
| Рис. 7. Функция плотности логарифмически-нормального закона. | 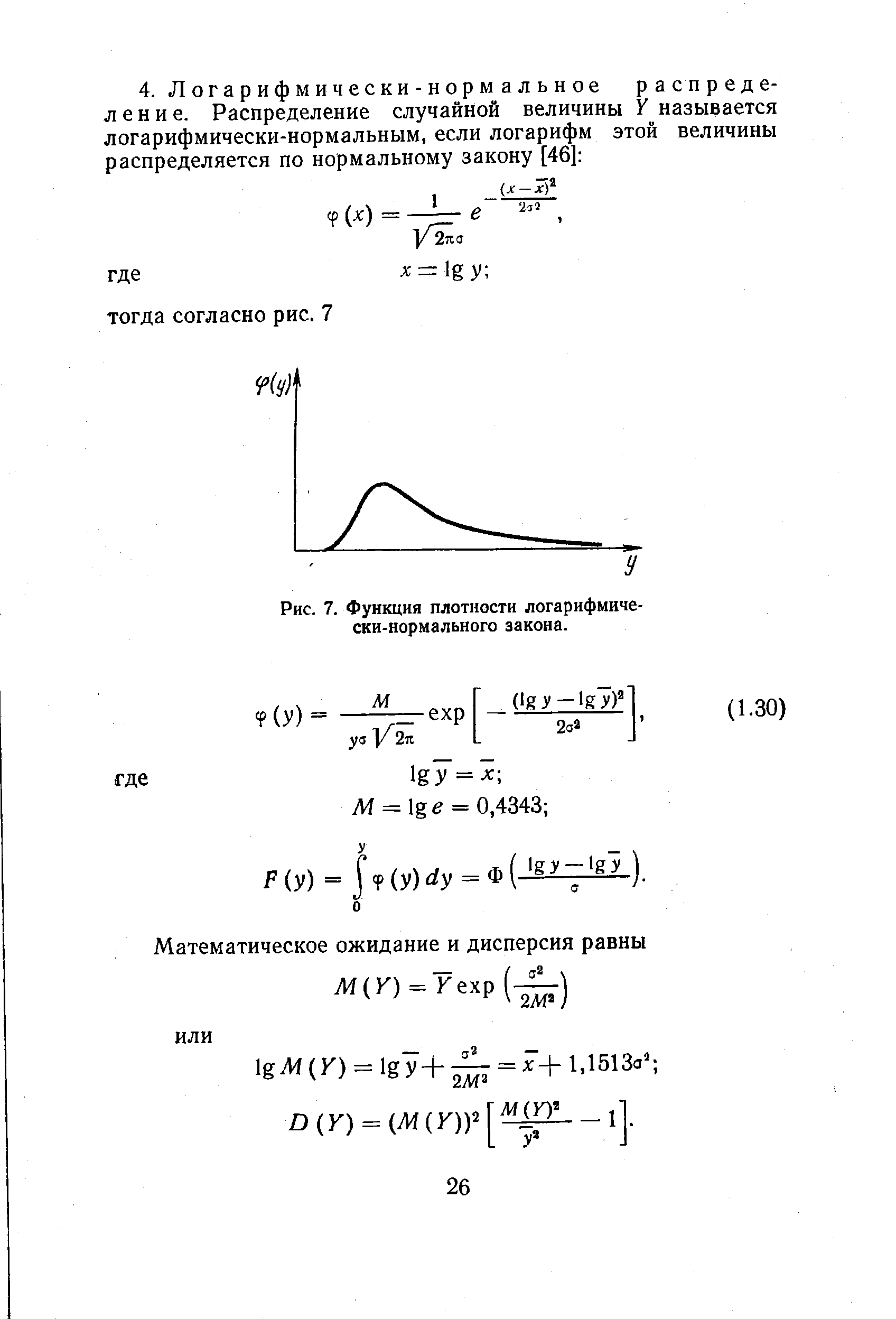 |
| Рис. 8. Функция плотности усеченного нормального распределения. | 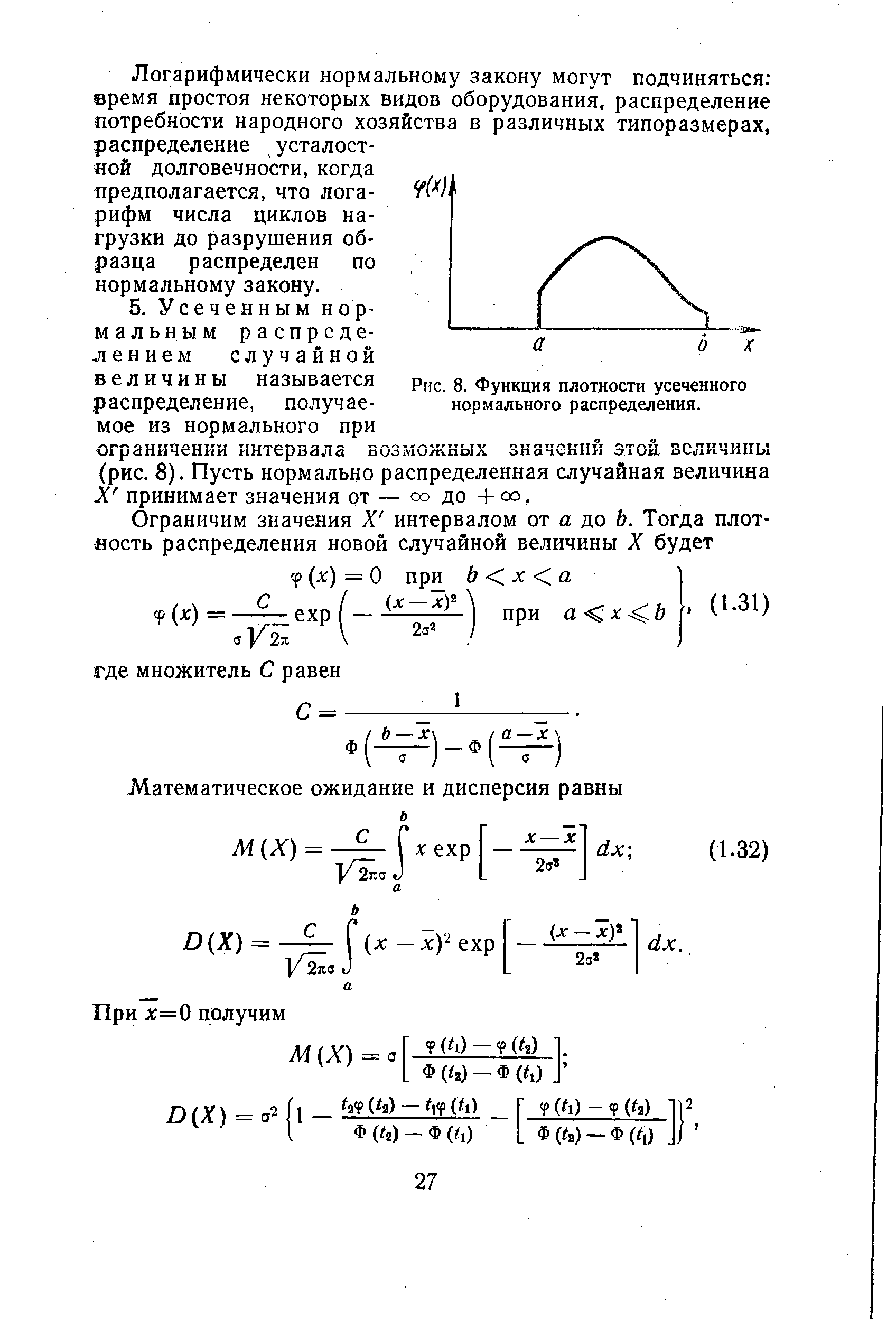 |
Модели, использующие начальное распределение потенциальных ресурсов. Они основываются на гипотезе о том, что значения функции плотности распределения неоткрытых запасов в любой момент времени пропорциональны площади между кривой начального распределения ресурсов и кривой распределения запасов, открытых к данному моменту. Начальное распределение запасов принимается логнормальным. [c.153]
Далее, исходя из функции плотности вероятности p(z), генерируют случайную совокупность (zt,. .., zn) размеров запасов месторождений в районе, которые будут открываться, такую, что [c.203]
Набор совокупности месторождений для каждой имитации.. Предполагается, что потенциальные ресурсы НГО оцениваются величиной R, распределение же месторождений по запасам характеризуется случайной величиной. При этом натуральные логарифмы величин запасов распределены по нормальному закону с математическим ожиданием ц и дисперсией ст2. Тогда функция плотности вероятностей величины запасов z имеет следующий вид [c.209]
Результаты расчетов параметров кривых распределения приведены в табл. 10. Расчетные частоты вычислялись по формулам 10, 11, 12. Объективной оценкой степени совпадения эмпирических и теоретических частостей является критерий согласия (в данном исследовании использовался критерий согласия В. И. Романовского [47, 88]). Проверка показала, что исследуемые эмпирические интервальные ряды распределения времени пролеживания предметов труда в переходящих заделах достаточно точно описываются найденными кривыми функции плотности р (х). [c.78]
| Рисунок 3- 7 Функция плотности нормального распределения вероятности | 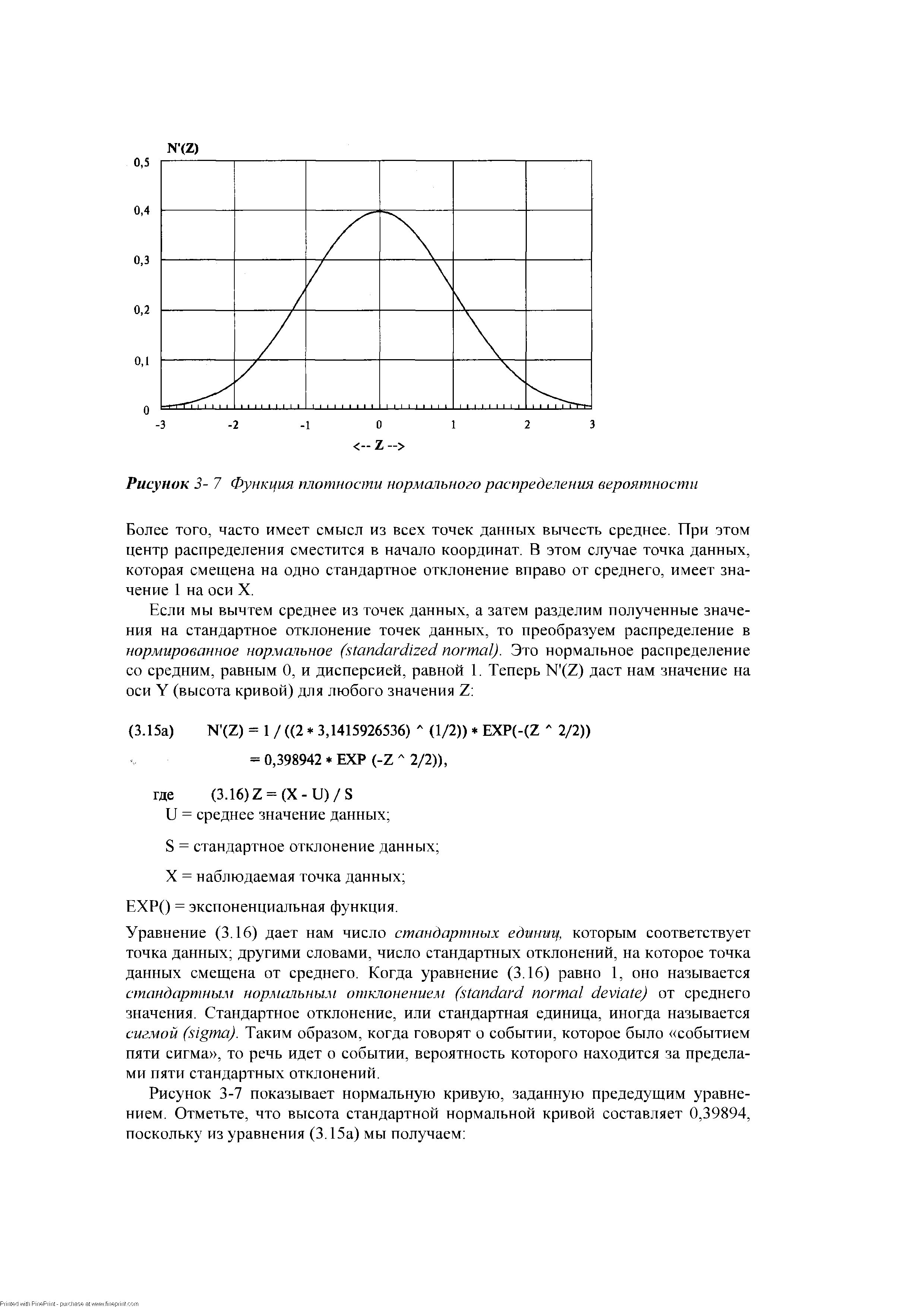 |
Данная глава посвящена моделированию фактического распределения сделок с помощью регулируемого распределения, то есть поиску функции и ее подходящих параметров, которые моделируют фактическую функцию плотности вероятности торговых P L с двумя точками перегиба. Вы можете использовать уже известные функции и методы, например, полиномиальную интерполяцию или экстраполяцию, интерполяцию и экстраполяцию рациональной функции (частные многочленов), или использовать сплайн-интерполяцию. После того как теоретическая функция найдена, можно определить ассоциированные вероятности тем же методом расчета интеграла, который использовался при поиске ассоциированных вероятностей регулируемого распределения, или рассчитать интеграл с помощью методов математического анализа. Одна из целей этой книги — позволить трейдерам, использующим немеханические системы, применять те же методы управления счетом, что и трейдерам, использующим механические системы. Регулируемое распределение требует расчета параметров, они относятся к первым четырем моментам распределения. Именно эти моменты — расположение, масштаб, асимметрия и эксцесс — описывают распределение. Таким образом, кто-либо, торгующий по немеханическому методу, например по волнам Эллиотта, [c.141]
| Рис. 154. Эволюция функции плотности вероятностей, представленная в проекции для переменной v в полной системе уравнений Лоренца, обеспечивающих упрощенную модель атмосферной динамики. Переменная v изображена вдоль горизонтальной оси так, что центром симметрии является начальное условие. Время t изображено вдоль вертикальной оси. По ходу увеличения времени (вверх), изначально "контрастное" распределение в t=0 расширяется, но затем демонстрирует повторное появление контрастности (на t=0,4), увеличиваясь и заостряясь. Позднее, распределение разбивается на две ветви переменная v либо значительно выше, либо ниже изначального значения, тогда как прогноз в среднем предсказывает значение посередине, чего на самом деле, почти никогда не происходит. Это иллюстрирует фундаментальные ограничения прогнозов, основанных на одном репрезентативном значении. Источник [388]. | ![Рис. 154. Эволюция <a href="/info/4084">функции плотности вероятностей</a>, представленная в проекции для переменной v в полной <a href="/info/15297">системе уравнений</a> Лоренца, обеспечивающих упрощенную модель атмосферной динамики. Переменная v изображена вдоль горизонтальной оси так, что центром симметрии является <a href="/info/20412">начальное условие</a>. Время t изображено вдоль вертикальной оси. По ходу увеличения времени (вверх), изначально "контрастное" распределение в t=0 расширяется, но затем демонстрирует повторное появление контрастности (на t=0,4), увеличиваясь и заостряясь. Позднее, распределение разбивается на две ветви переменная v либо значительно выше, либо ниже изначального значения, тогда как прогноз в среднем предсказывает значение посередине, чего на самом деле, почти никогда не происходит. Это иллюстрирует фундаментальные ограничения прогнозов, основанных на одном репрезентативном значении. Источник [388].](/pic1/245045135016255005219012000041198111096048141171.png) |
Аргумент g преобразуют так, чтобы в окончательном виде оцениваемый параметр оказался заключенным между величинами, определяемыми по выборке. Это и будут границы доверительного интервала (0ip 0И). Функцию g (0, Qh) выбирают таким образом, чтобы она допускала подобное преобразование и имела известную (лучше табулированную) функцию плотности вероятностей/ ). Последнее обстоятельство существенно упрощает определение значений 8, и 8,. [c.53]
| Рис. 2.5. Функция плотности (распределения) и функция распределения | 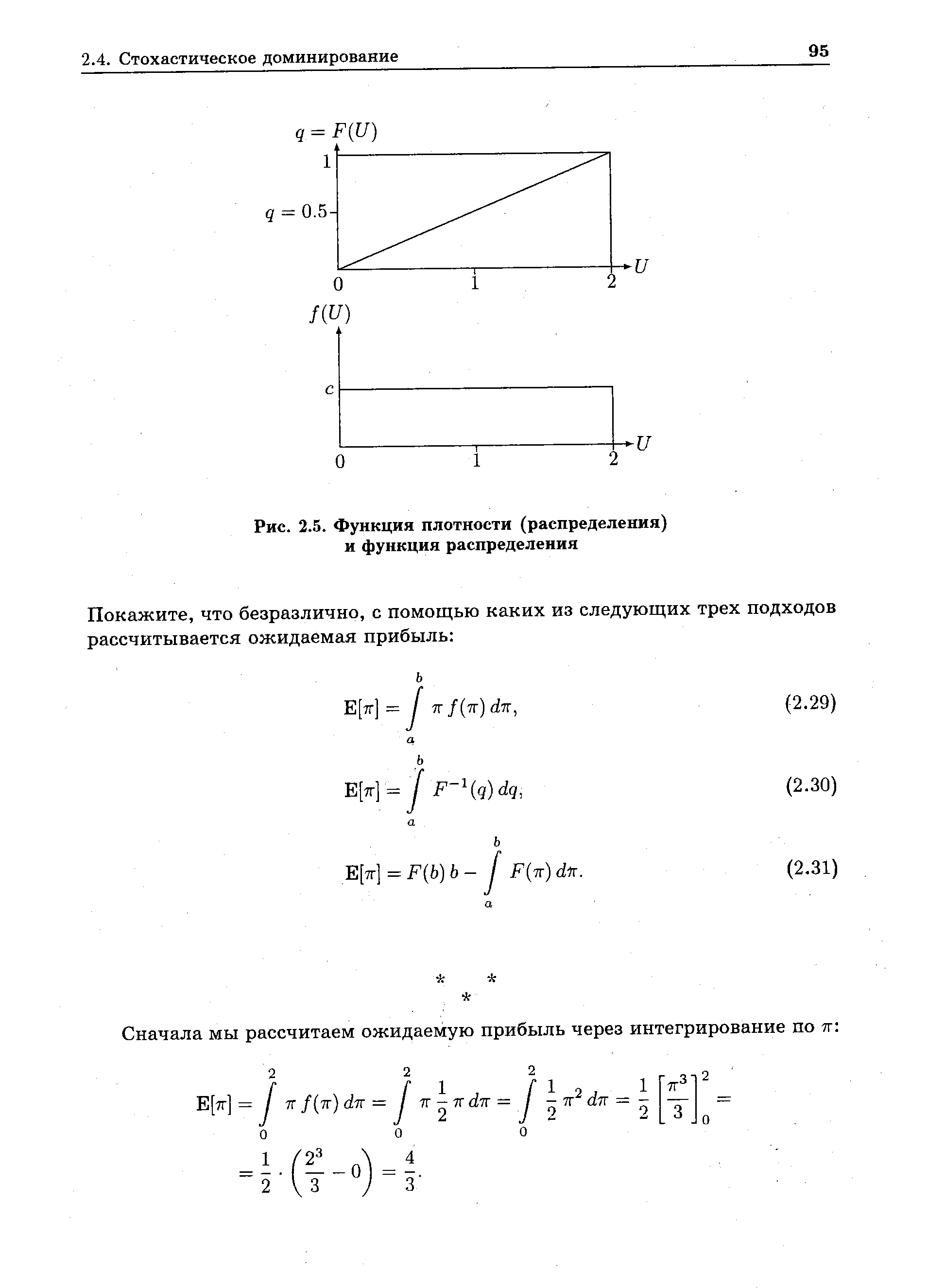 |
Изобразите функции плотности распределения, распределения и разности распределения графически. [c.101]
Был проведен анализ работы отечественной УЗК на Ново-Уфимском НПЗ для исследования уровня надежности реакторов. Практика показывает, что в современном производственном процессе наиболее слабым (и ответственным) звеном в технологической цепи УЗК являются реакторы. Следует отметить, что особое значение безотказного функционирования реакторов определяется их влиянием на отказ всей системы. Реактор УЗК представляет собой цилиндрический вертикальный пустотелый аппарат, снабженный верхним (полушаровым) и нижним (коническим) днищами с горловинами для ввода гидрорежущего инструмента и выгрузки кокса. Информация об отказах оболочки собрана из ремонтных журналов и дефектных ведомостей по эксплуатации УЗК. Анализ обработки статистической информации показал, что дифференциальная функция плотности распределения отказов реакторов подчиняется закону Вейбула. 1,0 [c.51]
Полагая т = Рдст1Р получим следующий вид функции плотности сглаживания (теоретически) нормального распределения [c.195]
На третьем этапе исследуются выборки, в которых гистограммы распределения времени пролеживания деталей и сборочных единиц на межцеховом складе могут быть аппроксимированы кривой распределения закона Шарлье [47, 84]. Функция плотности распределения закона Шарлье имеет следующий вид [c.77]
Подлинное страдание причиняла мне известная теорема об условных вероятностях, утверждавшая, что совместную плотность вероятности нельзя получить из безусловных плотностей вероятности компонент. Согласно традиционной точке зрения считалось, что в отсутствие стохастической независимости функция совместной плотности вероятности является уникальной, вполне самостоятельной, которая возникает как бы ниоткуда То есть она не выражается через функции безусловных плотностей составляющих, а есть новая, самостоятельная функция плотности вероятности, которая не может быть восстановлена из функций безусловных плотностей составляющих. Чтобы убедиться в этом, рассмотрим следующую таблицу, позаимствованную у Феллера, которую мы графически проиллюстрировали на рис. 3.1. [c.137]
| Рис. 38. Двумерные (линии уровня) и трехмерные графики распределения ценовых приращений в интервале 200 торговых дней, с центром 19 октября 1987 (соответствует О абсциссы). Масштаб плотности вероятности (ось Z) поверхностного участка логарифмический, что обеспечивает для прямого затухания экспоненциальное распределение. График изоквант (линий, на которых логарифм функции плотности вероятности принимает одинаковое значение) на верхней грани куба кодируется яркостью. Самая яркая область контурного участка соответствует наиболее вероятному значению. Символ R означает return (исход или приращение). Источник [267]. | ![Рис. 38. Двумерные (линии уровня) и <a href="/info/68612">трехмерные графики</a> <a href="/info/186383">распределения ценовых</a> приращений в интервале 200 торговых дней, с центром 19 октября 1987 (соответствует О абсциссы). Масштаб <a href="/info/57048">плотности вероятности</a> (ось Z) поверхностного участка логарифмический, что обеспечивает для прямого затухания <a href="/info/5307">экспоненциальное распределение</a>. График изоквант (линий, на которых логарифм <a href="/info/4084">функции плотности вероятности</a> принимает одинаковое значение) на верхней грани куба кодируется яркостью. Самая яркая область контурного участка соответствует наиболее вероятному значению. Символ R означает return (исход или приращение). Источник [267].](/pic1/138154024202029233183212150171108162190023120105.png) |
