| Рис. 8.2. Гистограммы распределения дефектов по их абсолютному | 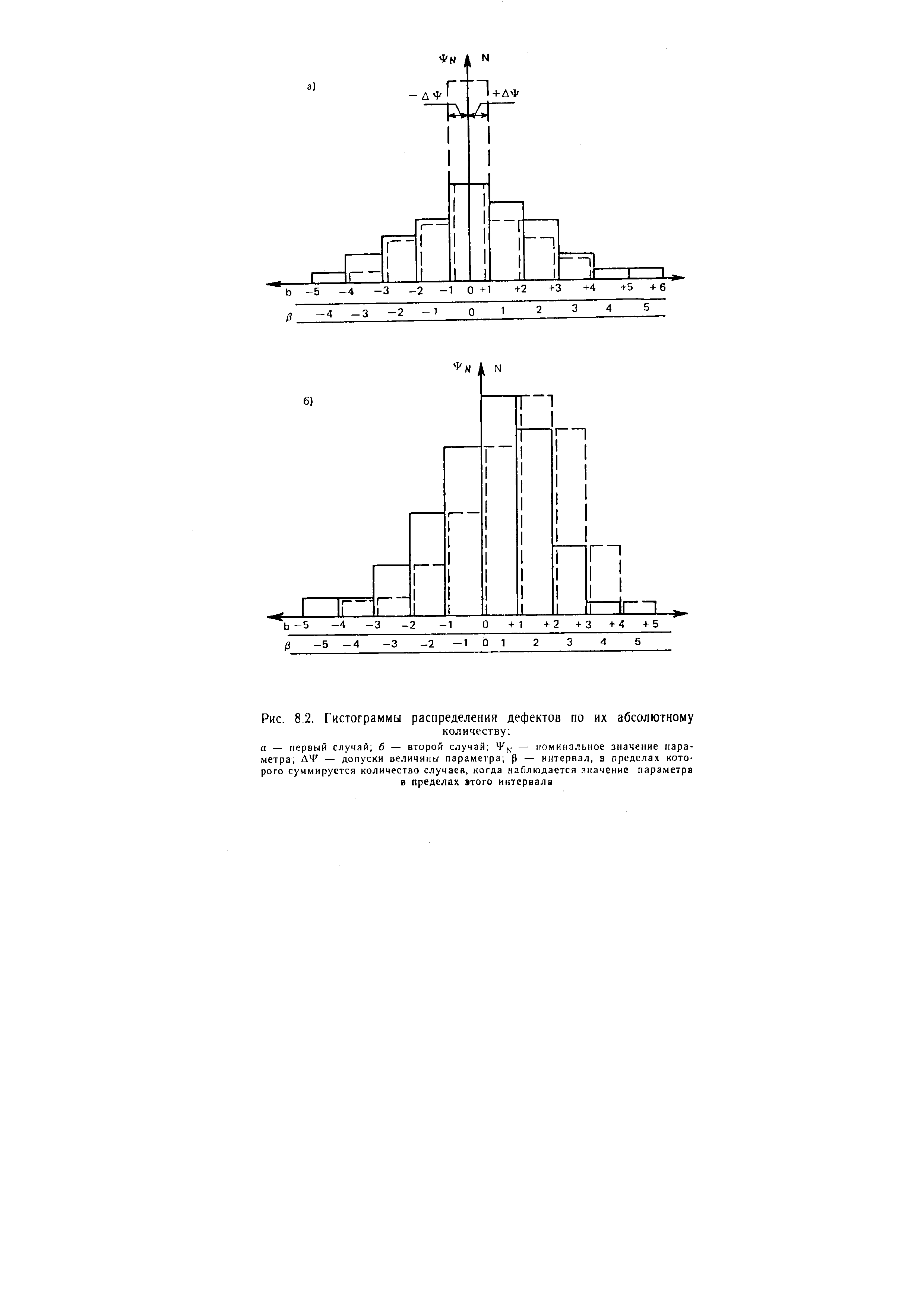 |
| Рис. 4. Гистограммы распределения продолжительности проходки скважин передовыми буровыми бригадами | 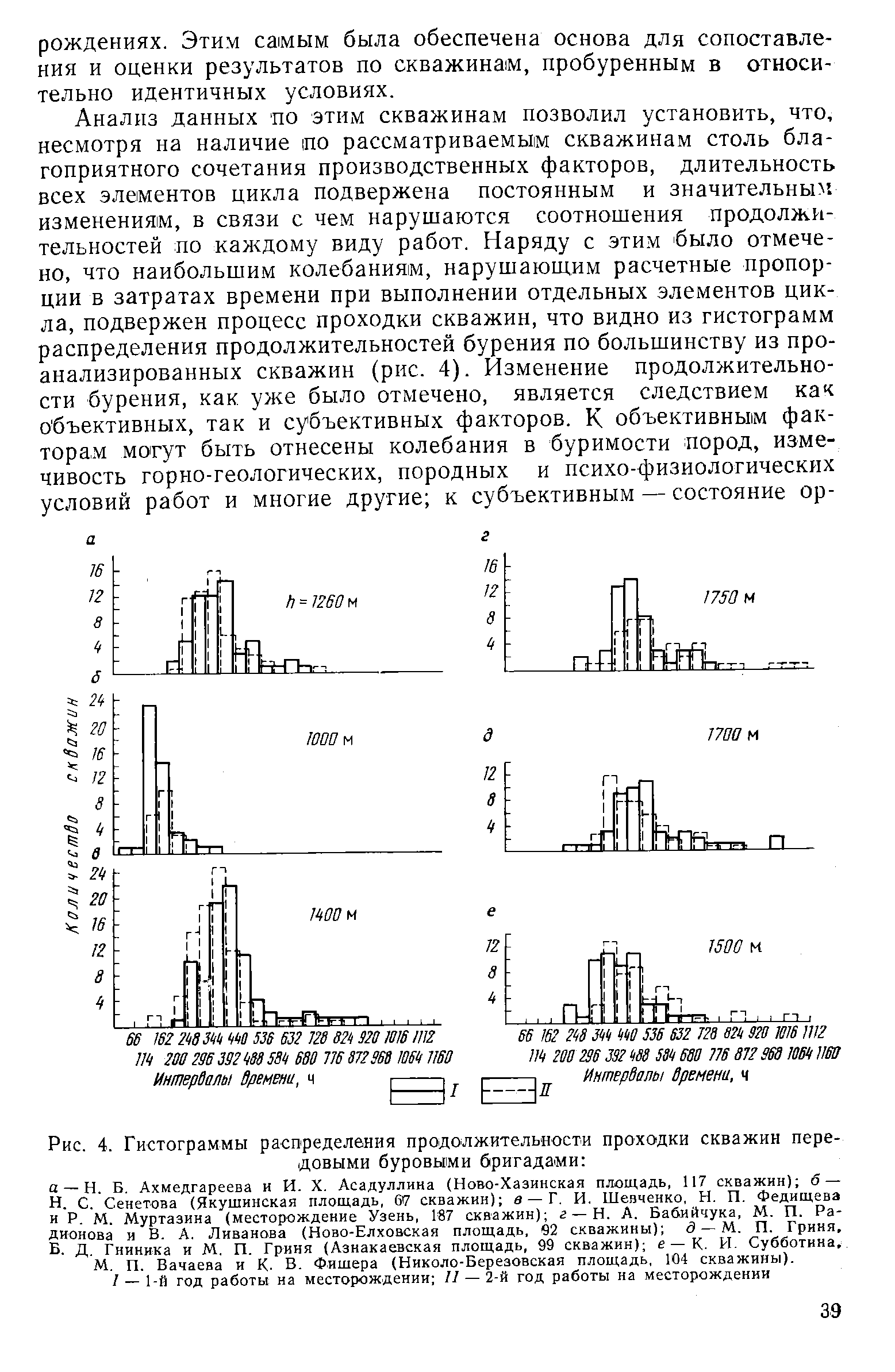 |
При построении гистограммы распределения вариационного ряда с неравными интервалами по оси ординат наносят не частоты, а плотность распределения признака в соответствующих интервалах. Это необходимо сделать для устранения влияния величины интервала на распределение и получения возможности сравнивать частоты. [c.32]
О выполнять статистическую обработку данных (построение рядов, гистограмм распределения, графиков сглаживания и т. п.) [c.472]
| Рис. 14. Гистограмма распределения времени пролеживания на складе деталей и выравнивающая ее показательная кривая. | 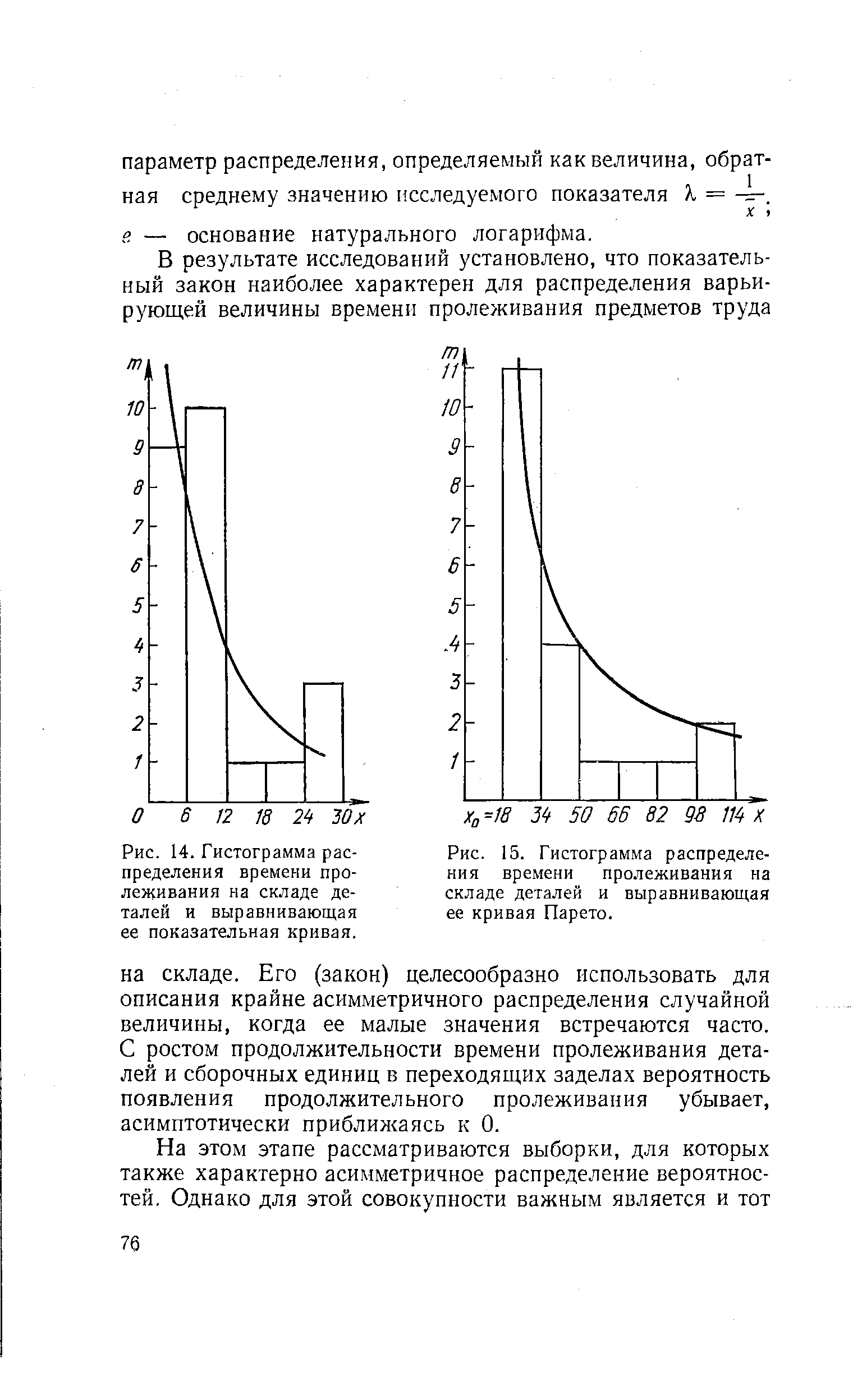 |
На рис. 16 приведена гистограмма распределения времени пролеживания детали вал изделия I. Аналогичные гистограммы получены и при исследовании пролеживания деталей пакет ротора изделия I и пакет статора изделия III. [c.77]
Подробно рассмотрена проблема группировки данных, то есть расчет оптимального количества интервалов группировки и оптимальной ширины интервала, а также построения по сгруппированным данным гистограммы распределения. [c.79]
Построение гистограммы распределения. [c.81]
Гистограмма распределения имеет 27 столбцов. Для большей наглядности плотность вероятности приведена не в виде гистограммы, а как плавная линия, проходящая через середины интервалов разбиения. [c.87]
После построения гистограммы распределения можно выдвинуть гипотезу о том, что данная гистограмма может быть аппроксимирована одним из изученных ранее законов распределения. При этом степень близости гистограммы и принятой аналитической модели может быть проверена с использованием критериев согласия. Здесь будет рассмотрен один из этих критериев - критерий Пирсона. [c.87]
| Рисунок 1. Гистограмма распределения управления | 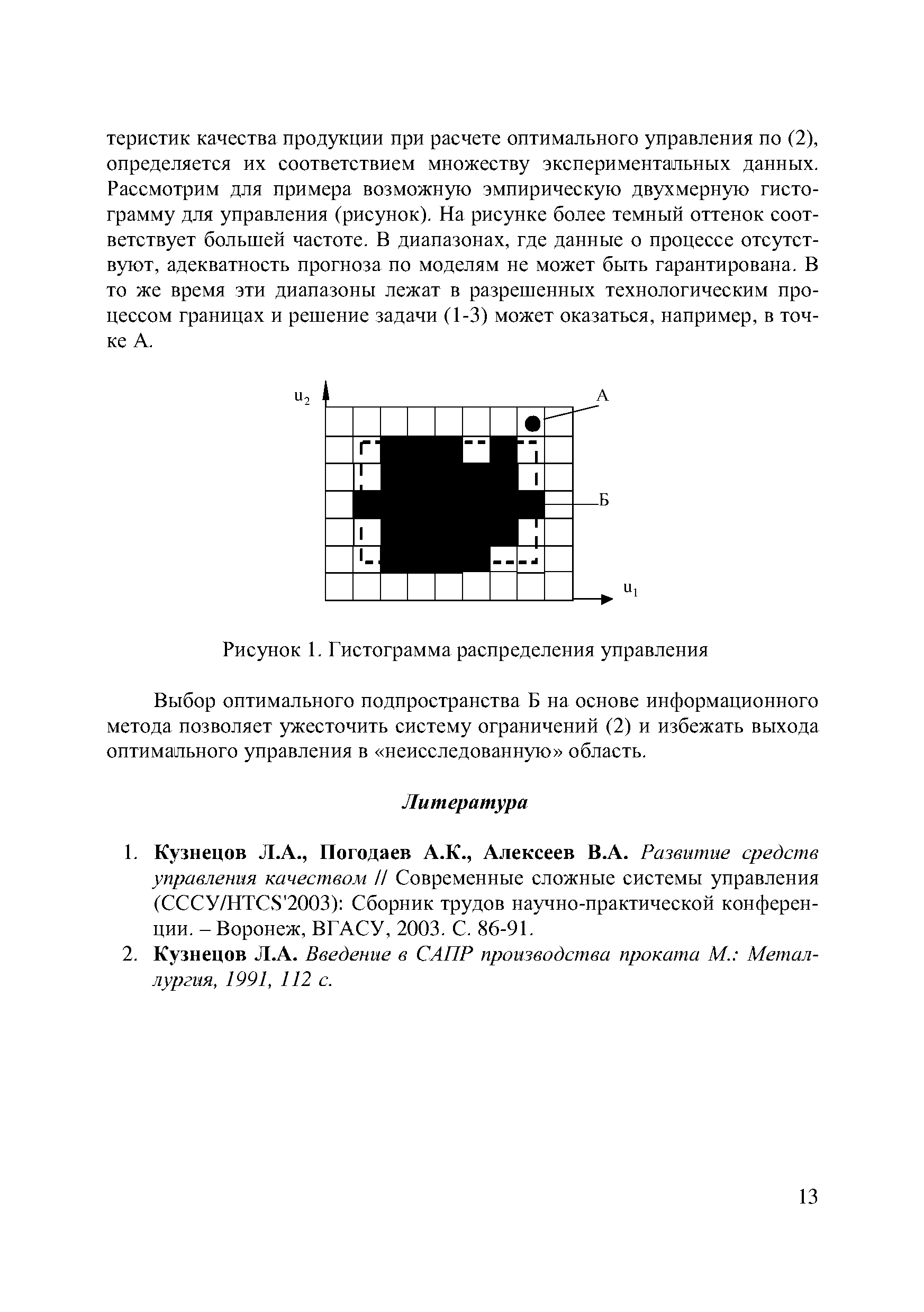 |
| Рис. 2. 2. Гистограмма распределения нитратов в огурцах. | 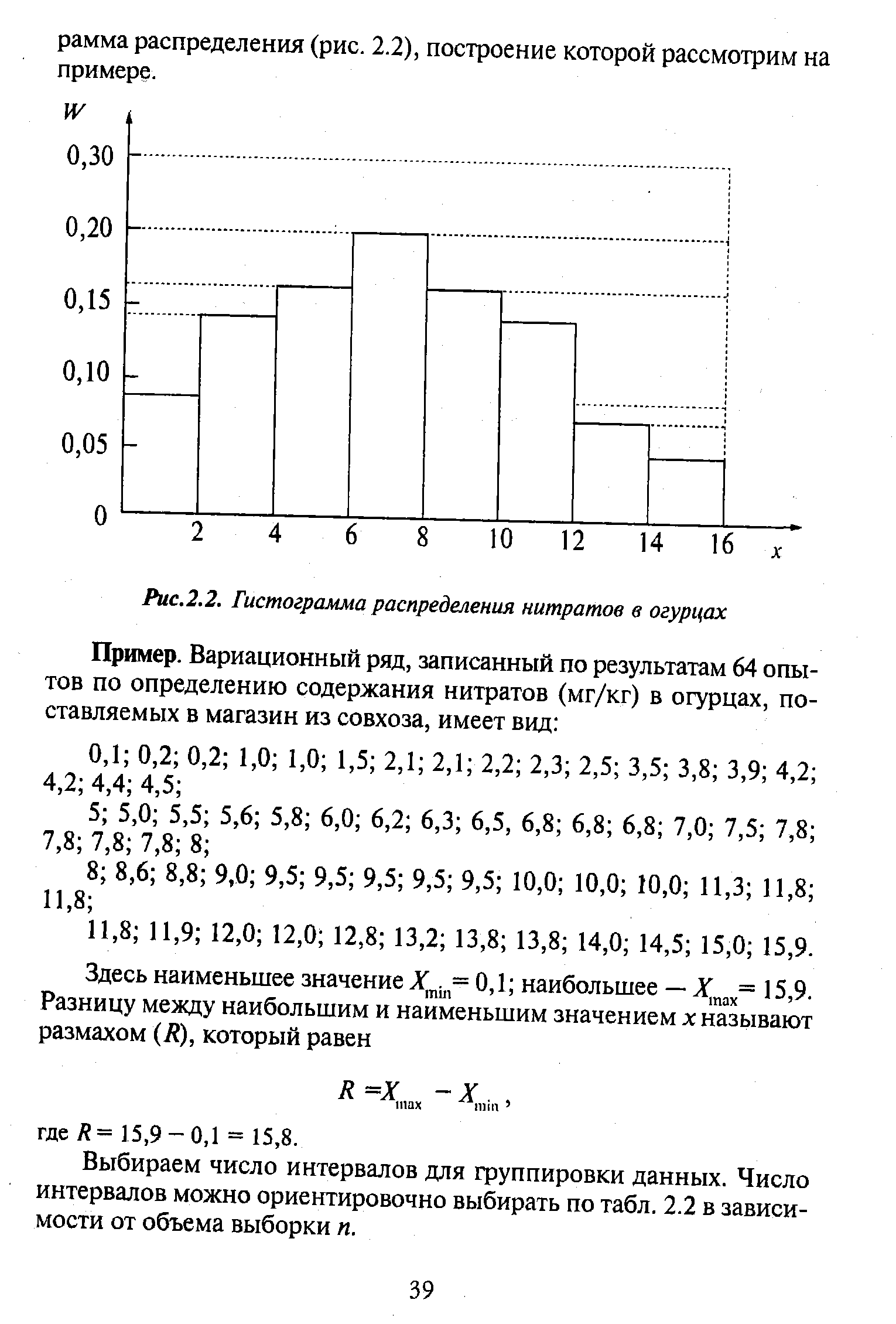 |
Если хорошее среднее получено в широком диапазоне значений, то каждый отдельный показатель может быть очень далек от оптимального значения. Другими словами, чем больше неопределенность, тем больше риск. Приемлемым отклонением можно считать величины в пределах 20% среднего значения. Большую пользу менеджерам приносит гистограмма распределения показателей. Наиболее благоприятной является ситуация, при которой гистограмма имеет один пик, и все значения показателя группируются вокруг среднего значения, которое приблизительно совпадает с пиком. Величина неопределенности характеризует ширину пика. [c.112]
Далее строим гистограмму распределения (рис. 4.19). Обведем гистограмму плавной кривой и получим вид выборочного распределения. Теперь можно вычислить параметры распределения среднее значение дисперсию среднеквадратичное отклонение. [c.160]
| Рис. 22.1. Гистограмма распределения спроса |  |
| Рис. 10. Гистограммы распределения заработной платы за 1966, 1957, 1959 и 1964 годы | 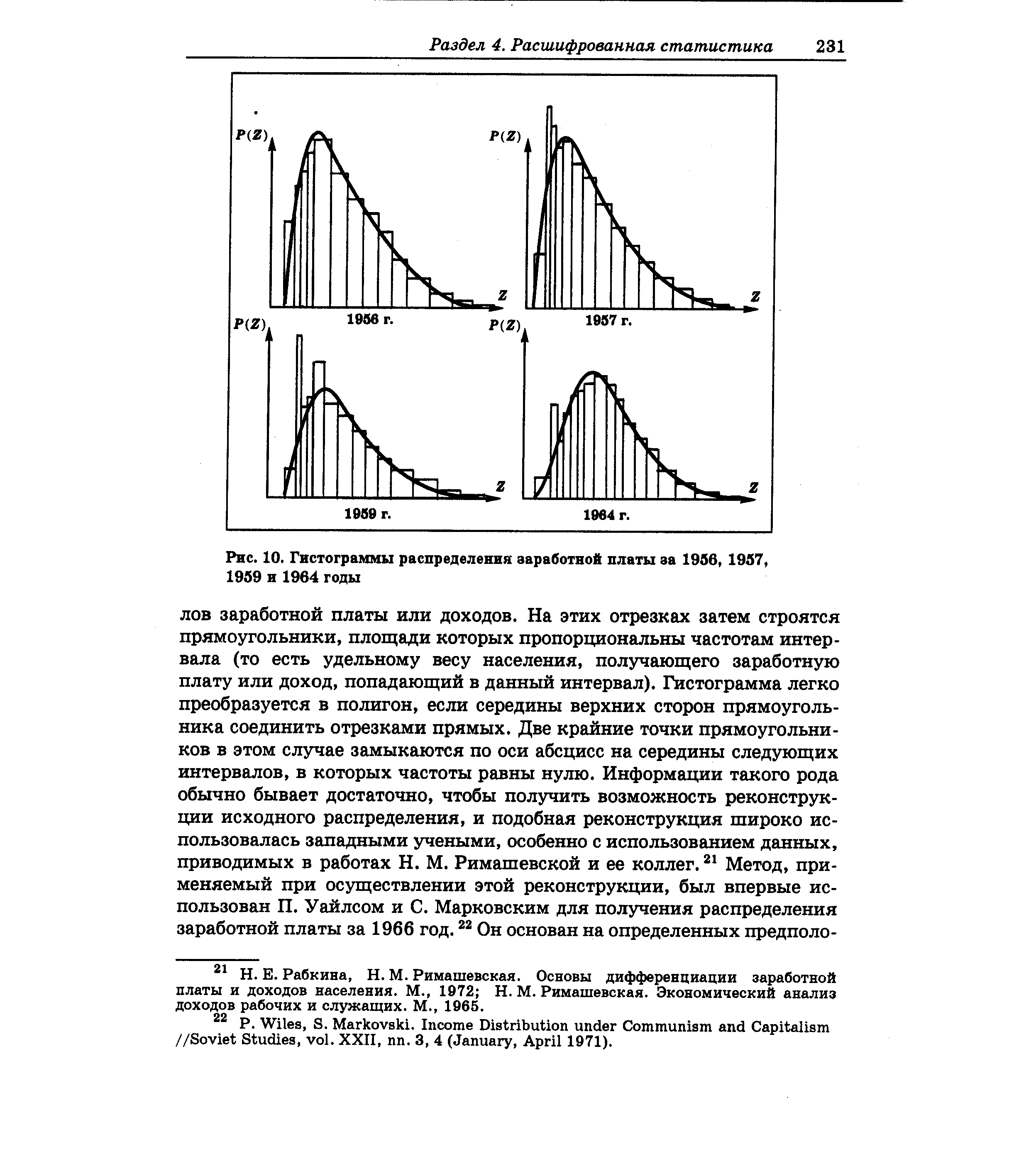 |
Гипотеза абсолютного дохода / 33 Гипотеза естественного уровня / 33 Гипотеза естественного уровня безработицы / 33 Гипотеза жизненного цикла 133 Гипотеза М. Фридмена / 33, 322 Гипотеза относительного дохода 133 Гипотеза перманентного дохода 133 Гипотеза решения 133 Гипотеза структурных изменений 133 Гипотеза Шумпетера 133 Гипотеза эффективного рынка 134 Гистограмма 134 Гистограмма распределения 134 Гиффена парадокс и товары 134 ГКО 134, 189 [c.781]
Гистограмма распределения реализаций случайной величины применяется для графического изображения интервальных рядов распределения. Она представляет собой многоугольник, построенный с помощью смежных прямоугольников. В случае непрерывных равных интервалов с шириной интервала Ах гистограмма строится следующим образом (рис. 1.3). [c.19]
Гамма-распределение 31 Гармонический фильтр 162 Гистограмма распределения 19, [c.424]
Анализ данных по этим скважинам позволил установить, что, несмотря на наличие по рассматриваемым скважинам столь благоприятного сочетания производственных факторов, длительность всех элементов цикла подвержена постоянным и значительным изменениям, в связи с чем нарушаются соотношения продолжи-тельностей по каждому виду работ. Наряду с этим было отмечено, что наибольшим колебаниям, нарушающим расчетные пропорции в затратах времени при выполнении отдельных элементов цикла, подвержен процесс проходки скважин, что видно из гистограмм распределения продолжительностей бурения по большинству из проанализированных скважин (рис. 4). Изменение продолжительности бурения, как. уже было отмечено, является следствием как объективных, так и субъективных факторов. К объективным факторам могут быть отнесены колебания в буримости пород, изме-чивость горно-геологических, породных и психо-физиологических условий работ и многие другие к субъективным — состояние ор- [c.39]
Регрессионная программа позволит сгенерировать серию выборочных наблюдений величины произвольного, заранее выбранного объема. Вот как, например, выглядит гистограмма распределения Z, полученная с помощью программы E onometri Views [c.286]
На третьем этапе исследуются выборки, в которых гистограммы распределения времени пролеживания деталей и сборочных единиц на межцеховом складе могут быть аппроксимированы кривой распределения закона Шарлье [47, 84]. Функция плотности распределения закона Шарлье имеет следующий вид [c.77]
| Рис.3. Гистограмма распределения величин критериев в каждом техноло- |  |
Выборочные данные группируют по интервалам, составляют гистограммы распределений и затем вычисляют различные статистики - количественные показатели, характеризующие пространственное распределение изучаемого явления. Наиболее употребительные показатели - среднеарифметическое, среднее взвешенное арифметическое, среднеквадратичное, дисперсия, вариация и др. Кроме того, с цомощью специальных показателей (критериев согласия) можно оценить соответствие данного конкретного распределения тому иди иному теоретическому закону распределения. Например, установить, согласуется ли эмпирическое распределение высот рельефа с кривой нормального распределения или подчиняется какой-либо иной функции. [c.222]
Для определения значения Л з на практике автор предложил использовать частотные гистограммы распределения величины х. Анализ фактических документов показал, что площади ряда текстовых реквизитов подчиняются гипергеометрическому закону распределения1. Решение уравнения (2.2) для этого случая сводится к рассмотрению случайной целочисленной величины, принимающей значения О, 1,2,... с вероятностями, характерными для данного закона распределения. [c.43]
Если из процесса извлекаются малые выборки фиксированного объема и строится гистограмма распределения числа дефектных изделий, обнаруживаемых в каждой выборке, наблюдается однохвостовое распределение, где большинство выборок содержит нулевой брак, следующая за ней категория — только одно дефектное изделие, следующая-—два дефектных изделия. Если размер распределения значительно возрастает, гистограмма распределения частот числа дефектных изделий в каждой выборке будет несимметричной, но все же будет иметь два хвоста, а вершина распределения — вблизи среднего числа дефектных изделий в выборке. Это распределение частот не описывается нормальным распределением, но, как было установлено, может быть описано биномиальным распределением. [c.129]
Как указывалось (раздел 7.9), гистограмма распределения частот может быть описана распределением Пуассона. Можно использовать Пуассонову диаграммную бумагу для построения карт, показывающих уровень вероятности, соответствующий пределам корректировки и предупреждения для любой вероятности, а не только для уровней За и 2сг, которые обычно используются. Можно также использовать таблицы для построения пределов корректировки и предупреждения при любых заданных вероятностях. [c.132]
Смотреть страницы где упоминается термин Гистограмма распределения
: [c.11] [c.83] [c.240] [c.145] [c.145] [c.160] [c.39] [c.39] [c.234] [c.134] [c.20]Математические методы моделирования экономических систем Изд2 (2006) -- [ c.19 , c.38 ]
