Следовательно, кривая нормального распределения может быть построена по двум параметрам - средней арифметической ц, и среднему квадратическому отклонению а. [c.197]
Значение ординат кривой нормального распределения/ можно получить по таблицам значения функции [c.198]
| Рис. 10.5. Кривая нормального распределения Гаусса для значений функций долевого участия собственных средств | 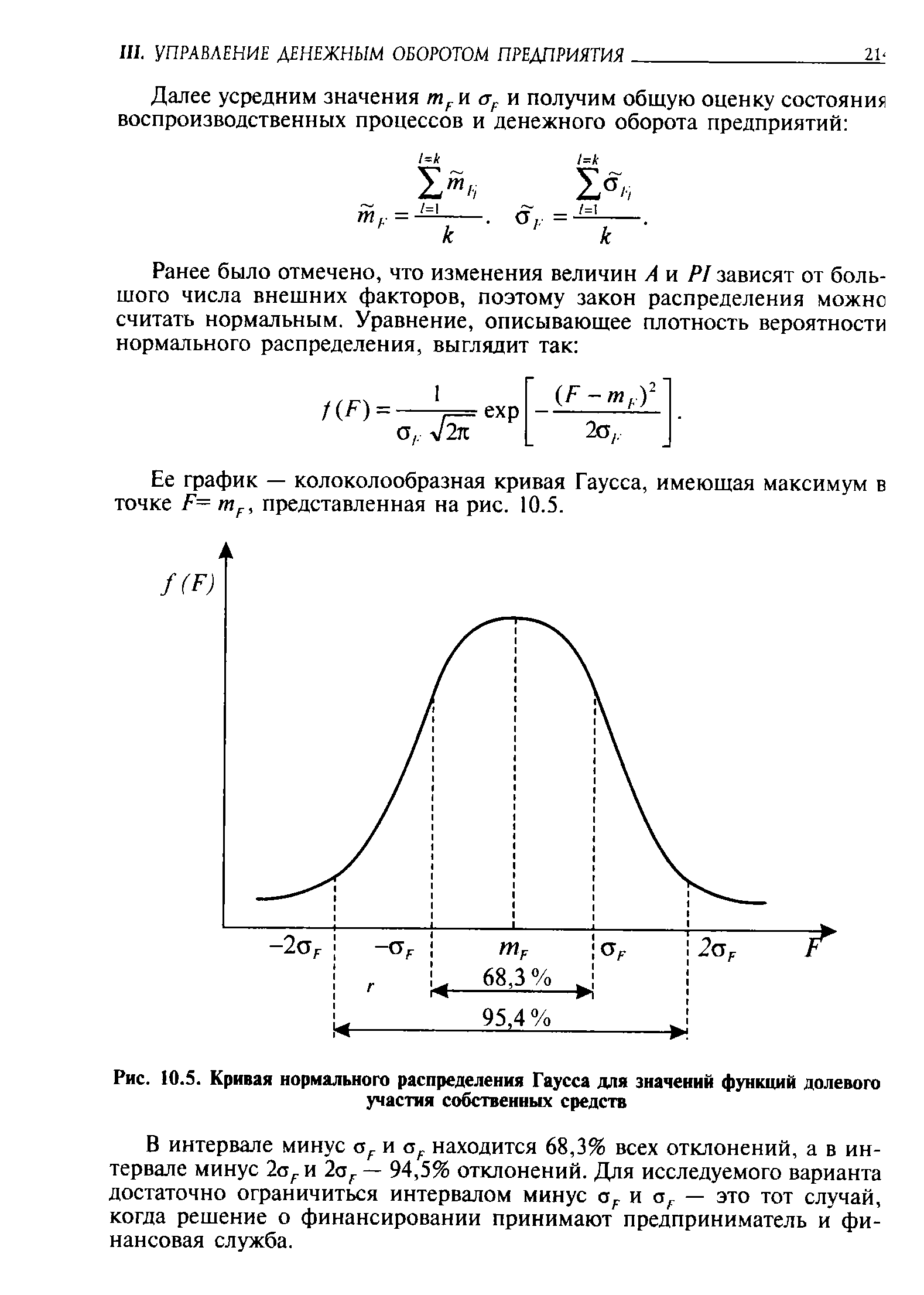 |
Принимаем, что плотность распределения смешанных случайных величин стремится к нормальному закону распределения. Предельную точку кривой нормального распределения выражаем через функцию Лапласа [c.91]
Кривые распределения, построенные по фактическим данным, сравнивают с кривыми нормального распределения. Для построения кривых нормального распределения следует использовать формулу [c.189]
Я сам, наряду с другими, потерял довольно много денег, используя эту карту. Проблема заключается в том, что "Рыночный Профиль" основан на параметрической (линейной) статистике, а в частности, концепции кривой нормального распределения. Нормальное распределение и принципы применения стандартного отклонения просто несоответствующим образом объясняют поведения естественных систем или рынков. Мы, буквальным образом, "теряемся" на рынке. [c.164]
Счет Z затем переводится в доверительную границу, которая иногда также называется степенью достоверности. Площадь под кривой нормального распределения вероятности шириной в 1 стандартное отклонение с каждой стороны от среднего значения равна 68% всей площади под этой кривой. Преобразуем счет Z в доверительную границу. Связь счета Z и доверительной границы следующая счет Z является числом стандартных отклонений от среднего значения, а доверительная граница является долей площади под кривой, заполненной при таком числе стандартных отклонений. [c.16]
Динамику метода оптимальной фракции можно проиллюстрировать при помощи кривой нормального распределения. Оптимальная доля будет представлять собой верхнюю часть кривой с участками, нисходящими влево и вправо. В сценарии с подбрасыванием монеты инвестиция в 10% от общей суммы бросков приносила прибыли меньше, чем 25-процентная, а инвестиция 25% была более прибыльной, чем 40-процентная. Эти инвестиции приносили гораздо больше прибыли, чем можно было бы получить без использования схемы реинвестирования. Однако при увеличении процента риска по каждой сделке до 51 положительное ожидание оборачивалось убытками. Следовательно, торговля с завышенным процентом риска может привести к бедствию. [c.77]
Для удобства расчета вероятности при нормальном законе вводится понятие срединного (вероятного) отклонения. Срединное (вероятное) отклонение — половина длины участка под кривой нормального распределения, симметричного относительно центра рассеивания, в пределах которого сосредоточено 50 % вероятности (рис. 3.10). [c.138]
По данным задачи 21 проведите выравнивание ряда распределения населения по размеру среднедушевых денежных доходов по кривой нормального распределения. Постройте графики эмпирического и теоретического распределений. Оцените близость эмпирического и теоретического распределений, используя критерии согласия [Пирсона (хи-квадрат), Колмогорова или др.] [c.373]
Кривая нормального распределения [c.160]
Возьмем из таблицы три значения плотности вероятности, соответствующие изменению величины х на 1, 2 или 3<т. Учитывая, что вся площадь под кривой нормального распределения равна 1, эти значения плотно- [c.160]
Стандартное отклонение, а (сигма) — это показатель попадания в границы площади под кривой нормального распределения. [c.497]
Неслучайное отклонение — это отклонение в результате неслучайной причины. Неслучайные причины вызывают уплощение или, наоборот, вытягивание вверх кривой нормального распределения. Управление качеством направлено на устранение всех неслучайных причин. [c.497]
Построив зависимость выборочного среднего от частоты, получим кривую нормального распределения (рис. 4.18). Искомая вероятность равна отношению площади под кривой выборочного распределения (заштрихованной) к площади под всей кривой. [c.159]
Идея информационного метода определения закона распределения заключается в следующем. Так как оценка энтропии распределена по закону Гаусса, то гипотеза о совпадении эмпирического и предполагаемого теоретического распределения принимается, если вычисленное по результатам экспериментальных данных значение Я (х) будет находиться в пределах доверительного интервала кривой нормального распределения с параметрами М[Н] и >[Я]. Нормированная по среднеквадратическому отклоне- [c.28]
Рисунок иллюстрирует существенное отличие фактических данных (кривая А) от теоретического варианта (кривая Б), имеющего вид кривой нормального распределения. [c.347]
Для сравнения на каждом из приведенных графиков построена кривая нормального распределения (Т), вычисленная но числовым характеристикам вариаций соответствующего нормообразующего фактора — по его математическому ожиданию и среднеквадратическому отклонению (по формуле (3.1), приведенной в [11, с. 165]). Из построенных графиков хорошо видно, что эмпирическая и теоретическая плотности распределения значительно различаются между собой. Для подтверждения этого нами дополнительно была проверена нулевая гипотеза о соответствии эмпирической плотности распределения закону нормального распределения генеральной совокупности. Проверку осуществляли по критерию согласия %2 К. Пирсона при уровне значимости а = 0,05 на основе рекомендаций, изложенных в [16, с. 329]. Критические значения %2, полученные на [c.124]
Исследуя кривую нормального распределения, можно легко доказать, используя выражение (81), что для нормально распределенной величины более 99% всех величин лежат на участке m - 3 <з. Это так называемое "правило трех [c.137]
Решать интегральное уравнение для кривой нормального распределения достаточно трудоемко, значительно удобнее использовать таблицы Формула плотности для кривой нормального распределения имеет следующий вид- [c.72]
Рис 2А.З. Кривая нормального распределения вероятностей [c.73]
Возможно, человеческая смерть — лучший пример. Возьмите группу людей и посмотрите, как смертельные удары происходят совершенно случайно, точно так же, как случайными оказываются такие величины, как рост, размер обуви и так далее. Но возьмите большое число людей, и вы увидите кривую нормального распределения Мало по краям и много посередине. Именно так часто происходит и с рынком. [c.144]
| Рис. 18.2. Кривая нормального распределения и ВЦВ |  |
| Рис. 18.3. Кривая нормального распределения |  |
Магия кривой нормального распределения превращает хаос в порядок [c.155]
Кривая нормального распределения имеет форму симметричного колокола, как это изображено на рис. 4.3. [c.191]
Так как кривая нормального распределения по сути является графиком функции нормальной плотности частот, то уравнение, определяющее нормальное распределение, будет [c.192]
Высота от любой точки кривой до оси абсцисс представляет собой функцию плотности стандартизованной кривой нормального распределения. Уравнение функции плотности стандартизованного нормального распределения выглядит следующим образом [c.194]
Теперь перейдем к таблице и определим площадь под кривой между z = 0 и z — 0,25, которая равна 0,0987. Принимая во внимание, что кривая нормального распределения симметрична и вероятность падения z ниже нуля равна 0,5, определяем вероятность того, что z < 0,25 0,5 + 0,0987 = 0,5987. Соответственно вероятность того, что z > 0,25 (или доходность выше 0,525%) составит 0,4013, или 40,13% (1 - 0,5987 = 0,4013). [c.197]
Заметьте, что распределение Пуассона довольно симметрично, если имеет достаточно большое математическое ожидание, и в этой ситуации может быть аппроксимировано кривой нормального распределения. Это очень помогает во время работы над группами вероятностей, когда промежуточные вычисления становятся неуправляемыми. [c.207]
Уравнение (7.7) называют стандартным уравнением нормальной кривой. Величина/ достигает максимума при / = 0, в этом случае е 2/2 = 1. По мере увеличения / величина е 2/2 уменьшается, и соответственно уменьшается f(t). На рис. 7.1 приведен график кривой нормального распределения вероятностей. Ординаты на графике соответствуют вероятностям при том или ином значении /. Чтобы определить вероятность значений в интервале от /, до >2, следует найти отношение части площади кривой, заключенной между орди- [c.167]
Мы начнем с рисунка 8-1, на котором изображена гистограмма ежедневных значений доходности акций компании Digital Equipment в период с 1986 по 1988 г. На этот график мы накладываем конусовидную кривую нормального распределения. Результат типичен когда измерения проводятся для достаточно короткого интервала времени, значение нормы доходности любой акции в прошлом почти соответствует нормальному распределению2. [c.168]
И наконец, четвертый момент распределения, эксцесс (kurtosis) (см. рисунок 3-4), измеряет, насколько у распределения плоская или острая форма (по сравнению с нормальным распределением). Как и асимметрия, это безразмерная величина. Кривая, менее остроконечная, чем нормальная, имеет эксцесс отрицательный, а кривая, более остроконечная, чем нормальная, имеет эксцесс положительный. Когда пик кривой такой же, как и у кривой нормального распределения, эксцесс равен нулю, и мы будем говорить, что это распределение с нормальным эксцессом. Как и предыдущие моменты, эксцесс имеет несколько способов расчета. Наиболее распространенными являются [c.88]
В качестве иллюстрации вышесказанного на рис. 3.1 приведены эмпирические плотности распределения (Э) вариаций каждого из нормообразующих факторов (объемов суточного производства, объемов суточных отгрузок, интервалов отгрузок и т.н.), построенные на результатах расчетной обработки фактических условий формирования сбытового запаса комбайна КСК-100 в ПО Гомсельмаш 1. На график также нанесены теоретические распределения (Т) вариаций этих факторов, вычисленные из предположения, что они подчиняются нормальным распределениям. Расчеты для объемов суточного производства проведены по формуле (3.1), которая на основе обработки фактических данных позволяет получить кривую нормального распределения [c.123]
Нормальное распределение, хорошо описывающее многие практические ситуации, широко распространено на практике. Плотность распределения вероятностей симме трична относительно ожидаемой величины и имеет область определения от —оо до +оо На рис. 2А.З представлена кривая нормального распределения со средней доходностью, р., 10% и средним квадратическим отклонением, а, равным 5%. Любое нормальное распределение обладает следующим свойством площадь фигуры, ограниченной осью аб сцисс, графиком плотности распределения и прямыми, пересекающими ось абсцисс в точках ц а, составляет 68 3%, общей площади, лежащей между графиком плотности и осью абсцисс если прямые проходят через точки ц 2<г или ц Зет, доля площади увеличивается соответственно до 95 5 и 99.7%. Следовательно, вероятность того, что фактическая доходность будет колебаться в диапазоне от 5 до 15% (ц а), составляет 68.3%, и т. д. Очевидно, что чем меньше величина среднего квадратического отклоне ния, тем меньше вероятность слишком большого отклонения фактической доходности от ожидаемого среднего значения, а значит, и меньше общий риск инвестирования. Чтобы определить вероятность того, что результат будет меньше 7.5 и 12 5%, нужно вычислить площадь под кривой между этими точками, или заштрихованную площадь на рис. 2А.З Эта площадь может быть определена путем интегрирования или, еще проще, с помощью [c.71]
Есть еще кое-что, что может оказаться нам полезным, это кое-что называется профиль рынка , разработанный Питером Штейдлмайе-ром (Peter Steidlmeier). Данная концепция достаточно проста, в ее основе лежит кривая нормального распределения Кривая нормального распределения превращает хаос в порядок. Профиль рынка другой способ отображения динамики цен и объема. Известны также и прочие способы [c.57]
Применительно к своим системам я использую логику стопа . Ключевой момент — удерживать размер убытков на низком уровне. Таким образом, ключевым элементом является соотношение между точкой входа и уровнем стопа. Вот здесь и находит применение концепция отрицательного развития (ОР) — я всегда ставлю стопы за ОР. Я не хотел бы слишком много философствовать в пределах этой главы, но часто (обычно ) то, чего нет, является более важным чем то, что есть. Это можно пояснить на примере Шерлока Холмса и собаки, которая не лаяла . Великие музыканты говорят, что критическое значение имеют пробелы между нотами, а не сами ноты. ОР — это отсутствие развития. Работа Штейдлмайера заключается в трансформации хаоса в порядок. Это делает кривая нормального распределения. Развитие имеет место тогда, когда рынок проводит некоторое время на некотором ценовом уровне. ОР имеет место в случае, если рынок находится непродолжительное время либо во- [c.97]
Профиль рынка (ПР) — это метод организации рыночной информации способом, более полезным для тех, кто хочет, торгуя получать прибыль. Этот подход был разработан Питером Штедлмайером, и его гениальная идея проста- он всего лишь применил испокон веку известный статистический инструмент, кривую нормального распределения, к рынку Кривая нормального распределения всегда была чем-то магическим Возможно, она не превратит свинец в золото, но она превращает хаос в порядок. Если кто-то думает, что это — лишь красивые слова, посмотрите на рис. 18 1. [c.144]
