Нормальное распределение является одним из наиболее важных видов распределения вероятностей, используемых при принятии управленческих решений. Этот вид распределения можно обнаружить во многих практических примерах, и он особенно ценен при рассмотрении выборок из большой совокупности. Нормальное распределение, представленное на рис. 2.11, — симметричное, колоколообразное и может быть полностью определено значениями средней арифметической и среднеквадратического отклонения. Средняя арифметическая (ц) определяет центр распределения, а среднеквадратическое отклонение (ст) определяет его разброс. На рис. 2.12 показано, как разница в значениях средней арифметической влияет на положение графика, а на рис. 2.13 показано, как увеличение значения среднеквадратического отклонения меняет размах кривой. Однако, несмотря на изменение значений арифметической средней и среднеквадратического отклонения, базовая форма нормального распределения, определенная нормальной кривой, сохраняется. [c.78]
Определение участков под нормальной кривой требует сложной математической формулы. Данный процесс упрощается при использовании особых таблиц. Обычно это таблицы стандартного нормального распределения , где средняя арифметическая равна 0, а среднеквадратическое отклонение — 1. Любое нормальное распределение с заданной средней арифметической (ц) и заданным среднеквадратическим отклонением (а) можно привести к этому стандартизованному распределению с помощью следующей формулы [c.79]
Таблицы нормального распределения, как, например, те, что приведены в конце данного пособия, помогают определить участок под стандартной нормальной кривой за определенным значением i, как это видно на рис. 2.15. С [c.79]
| Рис. 2.14. Нормальная кривая, средняя арифметическая = 200, среднеквадратическое отклонение = 50 | 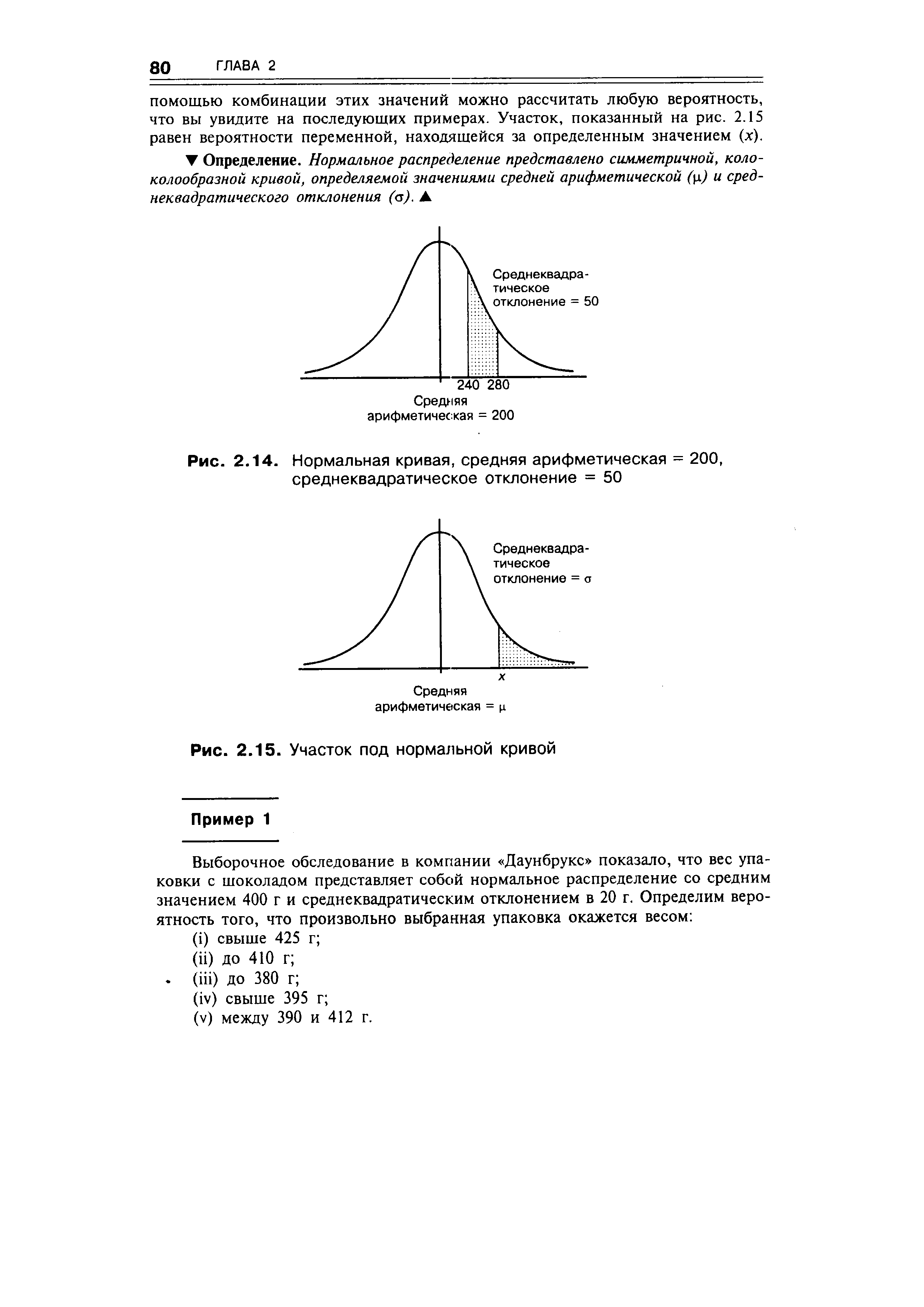 |
| Рис. 2.15. Участок под нормальной кривой | 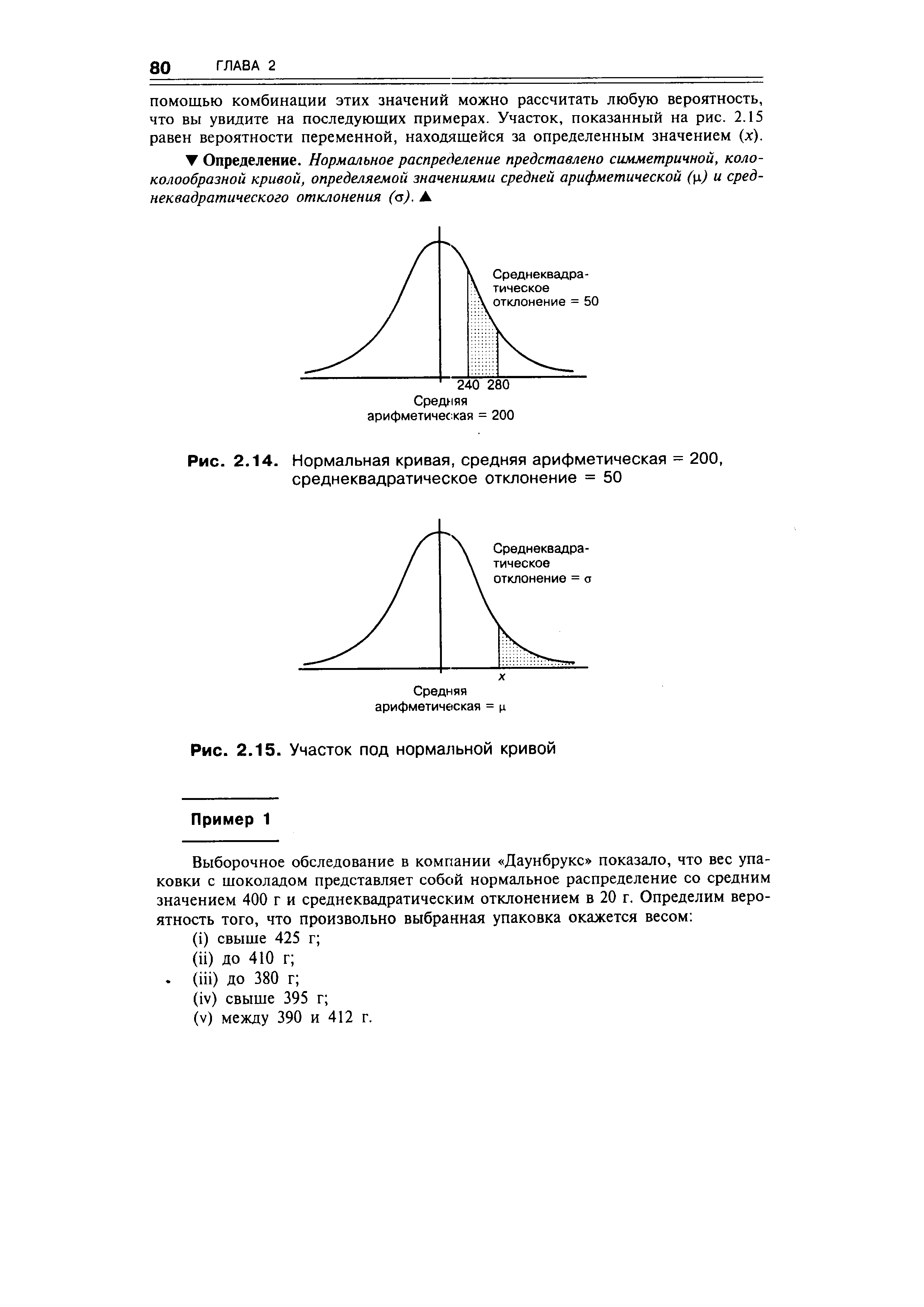 |
Следует отметить, что в данном примере сделано допущение, что количество баллов, набранных в ходе оценочного тестирования, есть непрерывная переменная, т. е. она может равняться любому значению в пределах заданного диапазона. Иначе говоря, количество баллов необязательно ограничено целыми числами, т. е. это может быть любое значение, например 52.6 или 49.861. В противоположность этому, если количество баллов считается дискретным , т. е. может быть только целым числом, то для использования нормального распределения при оценке вероятностей необходимо внести поправку на непрерывность . Например, вероятность получения 40 баллов определяется путем нахождения участка под нормальной кривой между 39.5 и 40.5. Аналогично, вероятность количества баллов между 40 и 50 находится на участке между 39.5 и 50.5. [c.84]
Е) Имеется нормальное распределение со средней арифметической, равной 40, и среднеквадратическим отклонением, равным 10. Найдите участок под нормальной кривой [c.84]
В этой главе мы также рассмотрели распределение вероятностей. В частности, нормальное распределение, определяемое значениями средней арифметической и среднеквадратического отклонения. Непрерывное распределение вероятностей играет важную роль, оно возникает в ряде реальных ситуаций и особенно полезно при рассмотрении результатов выборочного обследования. Например, независимо от формы распределения, очерчиваемой исходной совокупностью, при взятии больших выборок и определении значений средних эти средние имеют тенденцию, что является фактом, приближаться к нормальному распределению. Знание такого распределения позволяет оценить вероятности различных переменных, например результаты оценочных тестов, критические объемы производства, поступление пациентов и длительность реализации проекта. Далее, нормальное распределение можно использовать при прогнозировании вероятностного диапазона получаемых значений, что достигается путем оценки участков под нормальной кривой. Это лежит в основе некоторых прак- [c.93]
Участки под стандартной нормальной кривой [c.408]
При изменении только параметра а нормальная кривая перемещается вдоль оси Ох, при изменении [c.34]
Имея в виду табл. 9.2 и многие сотни наблюдений, имевшихся в распоряжении исследователей, которые провели эти расчеты, аналитик, возможно, подумает, следует ли применять выводы при небольшом числе дискретных наблюдений. Это может оказаться серьезной проблемой, и при наличии менее 20 наблюдений так называемое генеральное стандартное отклонение применять не следует. В этом случае прибегают к выборочному стандартному отклонению, которое исходит из наличия столь небольшого числа наблюдений, когда они полностью не описывают общую нормальную кривую и стандартные отклонения. [c.408]
Число nW должно быть достаточно большим, порядка 300 — 500. Так как случайная величина П является суммой многих случайных величин, то теоретически можно считать, что распределение ее будет следовать нормальному закону. Следовательно, будем выравнивать данное статистическое распределение нормальной кривой [c.197]
Наиболее распространенной теоретической кривой, описывающей симметричное распределение, является кривая Гаусса, называемая также нормальной кривой (фиг. 27). Ее уравнение [c.77]
Поэтому, чтобы подобрать нормальную кривую Гаусса, необходимо [c.79]
Построение суммарной кривой распределения D производится весьма просто, если функции N и Ф подчиняются нормальному закону распределения или мало от него отличаются. В этом случае, как доказывается в теории вероятностей, кривая распределения D будет также нормальной кривой. [c.81]
Нормальная кривая. Если инвесторы ожидают, что экономика будет развиваться равномерными [c.37]
| Рис. 56 Колоколообразная (нормальная) кривая |  |
| Рисунок 17. Кривая доходности сравнивает ценные бумаги, отличающиеся только своим временем погашения. Этот пример приведен для американских казначейских ценных бумаг и основан на сроках погашения и доходности, показанных в таблице. Доходность увеличивается по мере удлинения срока до погашения, поэтому кривая и вгибается направо вверх. Подобное поведение называется "нормальной кривой доходности. | 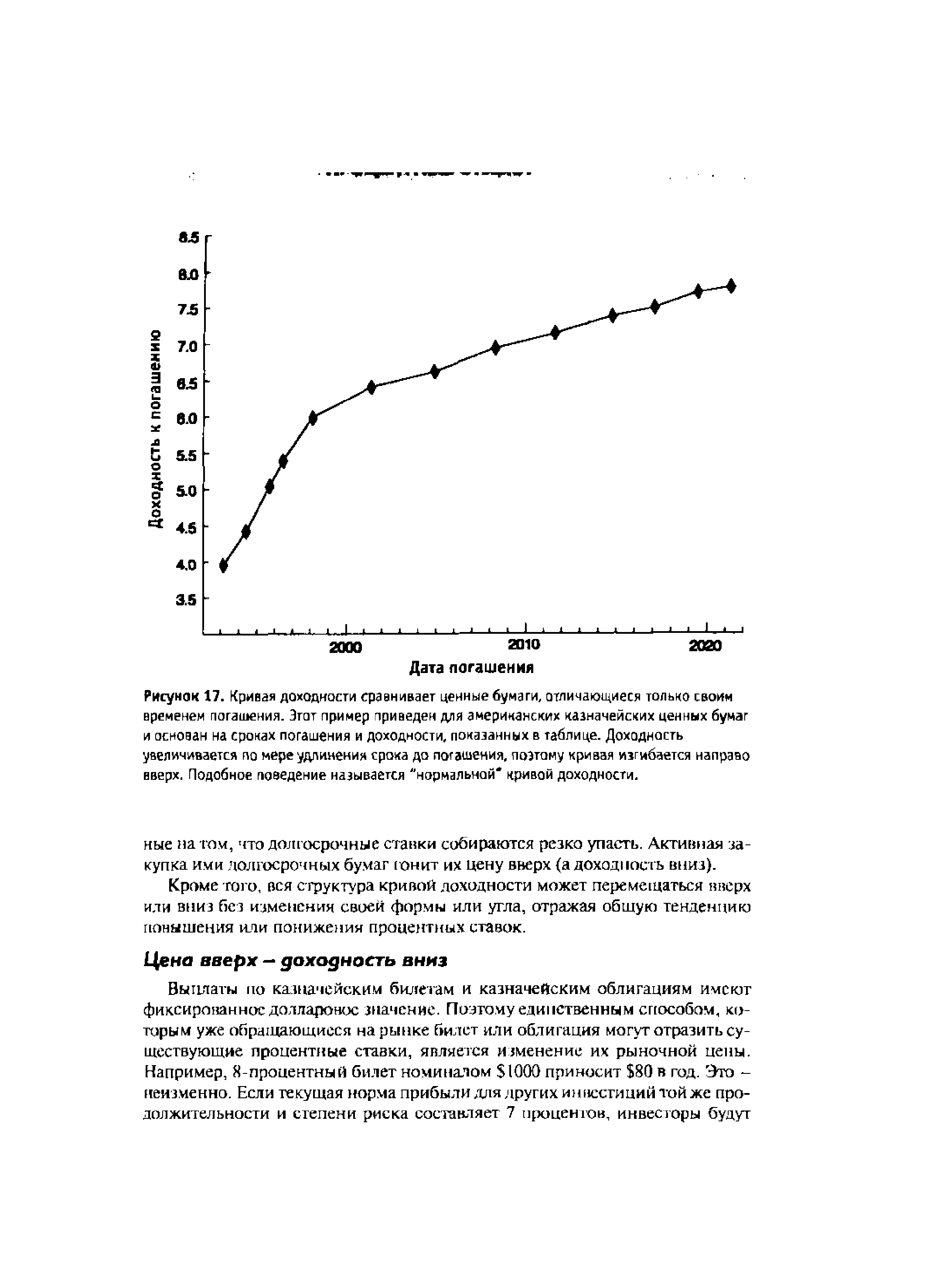 |
Нормальное распределение. Если распределение изменчивых величин происходит симметрично, то такое распределение называется нормальным >. Любая нормальная кривая полностью характеризуется двумя параметрами арифметической средней или средней арифметической величиной и мерой рассеяния или разброса, именуемой стандартным отклонением. Стандартное отклонение — это среднее квадратическое отклонение, равняющееся квадратному корню из средней арифметической квадратов отклонений индивидуальных значений наблюденных отклонений от их [c.292]
Значительный интерес представляет изучение нормальных кривых распределения сроков службы машин по физическому износу. Кривые показывают, какая часть общего количества изучаемых машин служит не меньше определенного количества лет. Так, из рис. 5.2 видно, что 75% рассматриваемых машин будет служить не менее 17 лет. [c.75]
| Рис. 5.2. Нормальная кривая распределения сроков службы машины по физическому износу |  |
В специальном случае, когда распределение доходов представлено нормальной кривой, инвесторы могут не беспокоиться об асимметрии и эксцессах, поскольку в этих условиях нет никакой асимметрии (нормальное распределение симметрично), а эксцесс нормального распределения, по определению, равен нулю. Рисунок 4.3 иллюстрирует распределение доходов двух инвестиций с симметричными доводами. [c.84]
Спрос на продукты при наличии внешних эффектов сетей имеет несколько особенностей, не присущих нормальным кривым спроса. Полезность продукта для каждого конкретного потребителя зависит от количества потребителей, которые покупают этот продукт, [c.312]
Стандартизованная функция плотности вероятностей нормальной кривой [c.171]
Таким образом, если выражение (4.25) определяется отдельно для всех возможных значений X, то при нанесении полученных точек на график в результате получится нормальная кривая. Мы рассмотрим это более подробно, когда займемся стандартизованными функциями плотности вероятностей. [c.192]
Стандартизованная ФУНКЦИЯ плотности вероятностен нормальной кривой [c.194]
Зависимость между стандартизованной и не стандартизованной функциями плотности нормальной кривой, данной в уравнении (4.25), становится очевидной. [c.194]
Нахождение функции в виде многочлена для приближенного описания кумулятивной нормальной кривой [c.373]
Нахождение ФУНКЦИИ в виде многочлена для приближенного описания КУМУЛЯТИВНОЙ нормальной КРИВОЙ [c.390]
Уравнение (7.7) называют стандартным уравнением нормальной кривой. Величина/ достигает максимума при / = 0, в этом случае е 2/2 = 1. По мере увеличения / величина е 2/2 уменьшается, и соответственно уменьшается f(t). На рис. 7.1 приведен график кривой нормального распределения вероятностей. Ординаты на графике соответствуют вероятностям при том или ином значении /. Чтобы определить вероятность значений в интервале от /, до >2, следует найти отношение части площади кривой, заключенной между орди- [c.167]
Как мы уже говорили в предыдущем разделе, вероятности могут быть путем определения участка под кривой. Итак, общая площадь пространства под любой нормальной кривой равна общей вероятности (= 1). Рассмотрим нормальную кривую со средней арифметической, равной 200, и сред неквад рати -ческим отклонением, равным 50. Это распределение представлено на рис. 2.14, а вероятность нахождения значения в пределах между 240 и 280 показана затемненным участком. [c.79]
Длительное продолжение добычи даже в условиях спада вполне возможно и повсеместно практикуется. Однако логарифмически нормальная кривая распределения Хабберта на практике замещается фрактальным распределением7. На поздних стадиях добычу можно продлить за счет разработки большого числа тех менее крупных месторождений и геологических структур, которые часто пропускают или не принимают в расчет при первичном, широкомасштабном исследовании продуктивной провинции. [c.58]
В нормальной кривой асимметрия и эксцесс равны нулю, а куртозис равен трем. Эти данные могут служить дополнительными признаками соответствия эмпирического материала нормальному закону Гаусса. [c.79]
Отложим на оси абсцисс твердости зубьев и построим нормальную кривую распределения, положив НВпт — /Y mm=6s, где s — стандарт кривой. Тогда кривые распределения твердости зубьев колеса и шестерни будут иметь вид, показанный на фиг. 29. [c.85]
Рисунок 3-7 показывает нормальную кривую, заданную предедущим уравнением. Отметьте, что высота стандартной нормальной кривой составляет 0,39894, поскольку из уравнения (3.15а) мы получаем [c.92]
Так как стандартное отклонение в стандартной нормальной кривой равно 1, мы можем сказать, что среднее абсолютное отклонение в стандартной нормальной кривой равно 0,7979. Более того, в колоколообразной кривой, подобной нормальной, семи-интер-квартильная широта равна приблизительно 2/3 стандартного отклонения, и поэтому стандартное отклонение примерно в 1,5 раза больше семи-интерквартильной широты. Это справедливо для большинства колоколообразных распределений, а не только для нормальных, как и в случае с преобразованием среднего абсолютного отклонения в стандартное отклонение. [c.94]
Контрольные карты. На контрольных картах по существу используются нормальная кривая и контрольные границы, показанные на нормальной кривой. Чаще всего используются контрольные карты арифметических средних (X) и контрольные карты р,азмаха (Я) (рис. 67). [c.293]
В случае ЕМН, теория была развита, чтобы оправдать использование статистических инструментов, которые требуют независимости или, в лучшем случае, очень краткосрочной памяти. Теория часто вступала в противоречие с наблюдаемым поведением. Например, согласно ЕМН частота изменения цены должна быть хорошо представлена нормальным распределением. Мы видели в Главе 2, что дело обстоит не так. Существует слишком много больших изменений, идущих и вверх и вниз, во всех частотах, чтобы приспособить эту нормальную кривую к этим распределениям. Однако такие большие изменения были обозначены как особые события или "аномалии" и не включались в частотное распределение. Результатом исключения больших изменений и перенормирования является нормальное распределение. Изменения цены были обозначены как "приблизительно нормальные". Альтернативы нормального распределения, например, устойчивое распределение Парето, были отклонены, даже несмотря на то, что они соответствуют наблюдаемым стоимостям без модификаций. Почему Стандартный статистический анализ не мог быть применен с использованием таких распределений. [c.49]
Херст работал в 40-х годах, когда компьютеры были всего лишь теоретической возможностью и уж определенно их не было в Египте. Херст пытался имитировать случайные лУждания подбрасыванием монеты, однако счел этот про-Чесс слишком медленным и утомительным. Вместо этого он готовил вероятностную колоду карт . Карты в ней были " Мечены числами -1, +1, -3, +3, -5, +5, -7, +7. Колода мела 52 карты, и числа были распределены таким образом, ° приблизительно давали нормальную кривую. Перетасо-351 колоду, снимая ее и замечая открытую карту, Херст [c.89]
