Т Определение. Пространство, лежащее под линией графика непрерывного распределения вероятностей, можно использовать для оценки вероятности переменной, находящейся между заданными пределами. А [c.78]
В этой главе мы также рассмотрели распределение вероятностей. В частности, нормальное распределение, определяемое значениями средней арифметической и среднеквадратического отклонения. Непрерывное распределение вероятностей играет важную роль, оно возникает в ряде реальных ситуаций и особенно полезно при рассмотрении результатов выборочного обследования. Например, независимо от формы распределения, очерчиваемой исходной совокупностью, при взятии больших выборок и определении значений средних эти средние имеют тенденцию, что является фактом, приближаться к нормальному распределению. Знание такого распределения позволяет оценить вероятности различных переменных, например результаты оценочных тестов, критические объемы производства, поступление пациентов и длительность реализации проекта. Далее, нормальное распределение можно использовать при прогнозировании вероятностного диапазона получаемых значений, что достигается путем оценки участков под нормальной кривой. Это лежит в основе некоторых прак- [c.93]
Непрерывное распределение вероятностей 76 [c.420]
Используя непрерывные распределения вероятностей, аналитик может отказаться от точной оценки каждого результата в отдельности. Вместо этого аналитик должен прочертить кривую, которая отразит ситуацию так, как он ее видит. Относительная вероятность каждого отдельного результата (скажем, доходов в расчете на акцию 1,035) равна нулю. Однако относительная вероятность любого диапазона доходов определяется путем простого измерения площади между кривой и горизонтальной осью. Так, вероятность того, что доходы окажутся в пределах от 1,03 до 1,04, может быть установлена при измерении площади под кривой между 1,03 и 1,04, что в данном случае составит приблизительно 0,07 (т.е. 7 шансов из 100, что в следующем году доходы будут в пределах 1,03 — 1,04). Для дискретных распределений вероятностей наподобие тех, что показаны на рис. 6.4 и 6.5, ранее отмечалось, что сумма вероятностей должна равняться 1,0. И тогда при непрерывном распределении вероятностей общая площадь под кривой должна составить 1,0. [c.153]
| Рис. 6.6. Непрерывное распределение вероятностей | 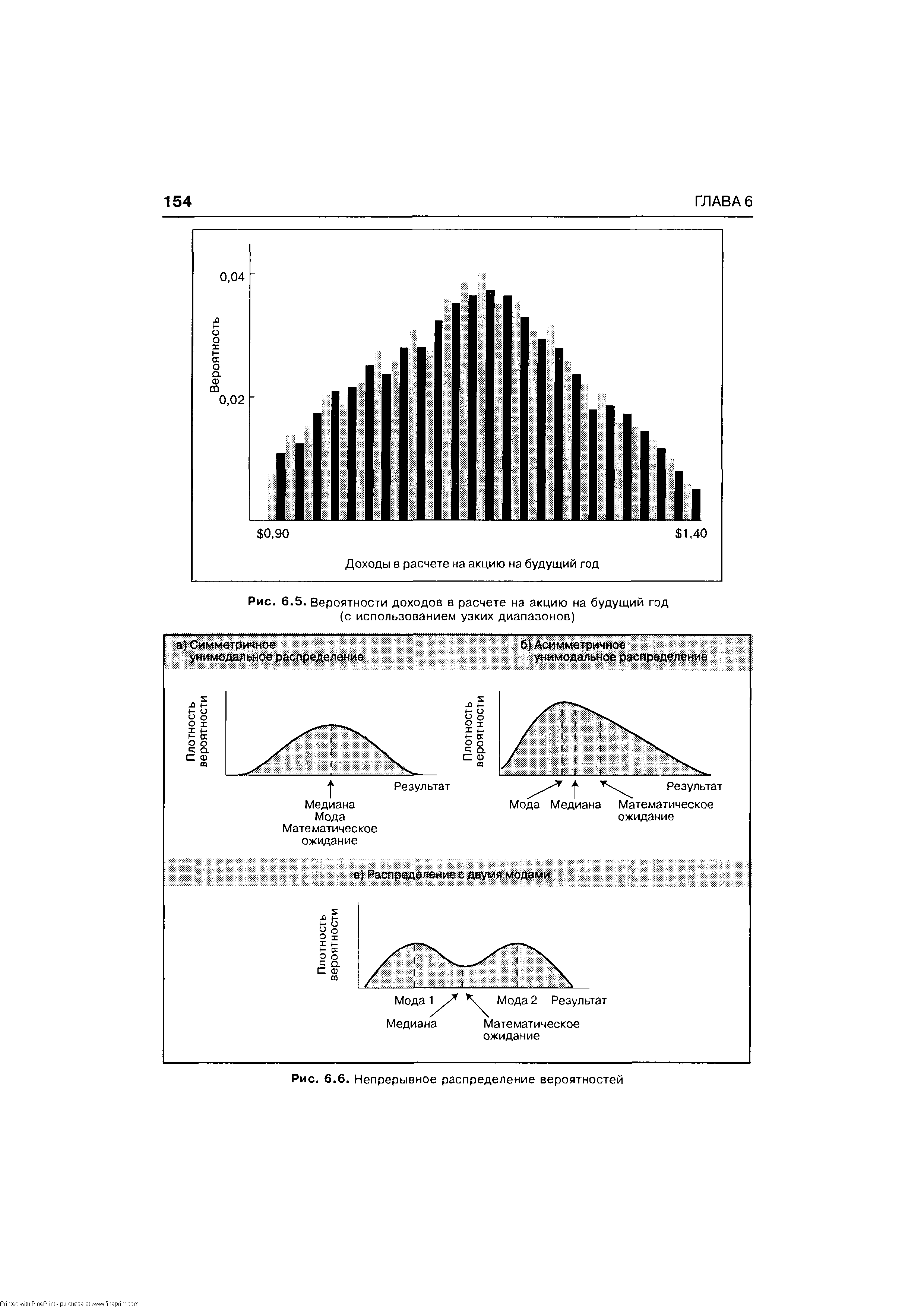 |
В реальном мире диапазон показателей доходности акций не ограничен несколькими значениями, как в нашем примере, и доходность может принимать практически любое значение. Поэтому мы можем сказать, что распределение доходностей акций представляет собой непрерывное распределение вероятностей. Чаще всего используется один из видов непрерывного распределения вероятностей — нормальное распределение, которое представляет собой кривую, показанную на рис. 4.13. [c.267]
Непрерывные распределения вероятностей [c.28]
Аналогичное выражение для ковариации при непрерывном распределения вероятности имеет громоздкий вид и здесь не приводится. [c.82]
Здесь важно отметить, что чем больше стандартное отклонение в распределении вероятностей, тем меньше вероятность того, что фактическая величина R окажется в пределах определенной зоны от средней величины. Лучше всего можно проиллюстрировать этот тезис не с помощью использовавшегося до сих пор дискретного распределения вероятностей, как на рис. 10.2, а посредством непрерывного распределения вероятностей, изображенного нормальной кривой (см. рис. 10.3). [c.339]
Для экзамена вам нужно знать, что есть несколько видов распределений вероятности, которые используются для записи информации относительно рисков. Вид распределения определяет тип информации, которую вы должны собрать в процессе интервью. Задачей данной книги не является рассмотрение распределения вероятности и связанных с этим вычислений. Запомните, что при количественном анализе риска используются непрерывные распределения вероятности. Согласно учебнику РМВОК непрерывные распределения включают в себя нормальное и логарифмически нормальное, треугольное, бета-распределение, равномерное распределение. Запомните также, что треугольное распределение основывается на пессимистичных, чаще всего, и оптимистичных оценках. Более подробно этот метод будет рассмотрен в 7 главе. Нормальное и логарифмически нормальное распределение используют среднее и стандартное отклонения. [c.238]
В реальном мире диапазон показателей доходности акций не ограничен несколькими значениями, как в нашем примере, и доходность может принимать практически любое значение. Поэтому мы можем сказать, что распределение доходи остей акций представляет собой непрерывное распределение вероятностей. Чаще всего используется один из видов непрерывного распределения [c.279]
В предыдущих разделах мы познакомились с дискретным распределением вероятностей, когда рассматриваемая переменная могла принимать только определенные (дискретные) значения. Например такие переменные, как количество брака, количество поступающих пациентов и количество несчастных случаев, могут быть выражены только целыми числовыми значениями. В этом разделе мы рассмотрим непрерывное распределение, когда теоретически переменная может иметь любое значение в пределах заданного диапазона. [c.76]
Следует отметить, что в данном примере сделано допущение, что количество баллов, набранных в ходе оценочного тестирования, есть непрерывная переменная, т. е. она может равняться любому значению в пределах заданного диапазона. Иначе говоря, количество баллов необязательно ограничено целыми числами, т. е. это может быть любое значение, например 52.6 или 49.861. В противоположность этому, если количество баллов считается дискретным , т. е. может быть только целым числом, то для использования нормального распределения при оценке вероятностей необходимо внести поправку на непрерывность . Например, вероятность получения 40 баллов определяется путем нахождения участка под нормальной кривой между 39.5 и 40.5. Аналогично, вероятность количества баллов между 40 и 50 находится на участке между 39.5 и 50.5. [c.84]
Для случайной величины с непрерывной и дифференцируемой функцией распределения вероятностей F(x) можно найти дифференциальный закон распределения вероятностей., выражаемый как производная F(x), то есть р(х) = dF(x)/dx. Эта зависимость называется плотностью распределения вероятностей. Плотность распределения р(х) обладает следующими свойствами [c.15]
Совместные вероятности двух непрерывных распределений [c.164]
Сценарные спектры можно представлять себе как дискретные распределения. Такой же подход можно использовать и для определения вероятностей для непрерывного распределения, если рассматривать его как дискретное распределение с бесконечно малым шагом квантования (т. е. с бесконечным множеством сценариев). [c.164]
Например, мы знаем, что центрированная нормально распределенная случайная величина с вероятностью 0,9772 не превышает двух стандартных отклонений, а с вероятностью 0,9986 — трех стандартных отклонений. Если один из сценариев спектра состоит в том, что нормально распределенная случайная величина попадает в пределы от +2 до +3 стандартных отклонений, то мы знаем, что вероятность этого сценария равна 0,0214 (0,9986 -0,9772). Значит, мы можем определять совместные вероятности для непрерывных распределений. Кроме того, мы можем сделать сценарий таким маленьким, как нам нужно. В упомянутом ранее примере мы можем использовать сценарий, который состоит в том, что нормально распределенная случайная величина попадает в пределы от +2 до +2,1 стандартных отклонений, или между +2 и +2,000001 стандартных отклонений. [c.164]
Укажите, в чем различие между непрерывными и дискретными распределениями вероятностей. [c.165]
Первый этап компьютерного моделирования — это задание распределения вероятностей каждой исходной переменной денежного потока, например цены и объема реализации. Для этой цели обычно используют непрерывные распределения, полностью задаваемые небольшим числом параметров (например, среднее и среднее квадратическое отклонение или нижний предел, наиболее вероятное значение и верхний предел варьирующего признака). [c.207]
Первый этап компьютерного моделирования состоит в задании распределения вероятностей каждой исходной переменной денежного потока, например цены и объема реализации. Для этой цели обычно используют Непрерывные распределения, полностью [c.169]
Интервал занятости — время непрерывной занятости прибора обслуживанием требований в системе массового обслуживания. И. з. — случайная величина, по распределению вероятностей которой можно судить о времени бесперебойной работы прибора, на которое он должен быть рассчитан. [c.428]
Наконец, мы не обнаруживаем никаких свидетельств непрерывного распределения доходности. Демонстрация этого факта представлена в таблице 6.4, где управляющие капиталом были разбиты по квартилям, после чего проанализирована вероятность перемещения из одного квартиля в другой в течение каждого года за период 1983-1990 гг. [c.193]
Аналогичные соображения применимы и в более общем случае — прц непрерывном распределении вероятностей для цены акций, лежащих в основе опциона. Доход от опциона на дату истечения неможет быть отрицательным. В худшем. случае опцион ничего не будет стоить и контракт не будет выполняться. Таким образом, распределение вероятностей для доходов по опционам при нуле обрезается. Это приводит к тому, что ожидаемые доходы по опционам растут тем больше, при неизменном значении ожидаемых (средних) доходов по акциям, чем больше изменчивость цены подлежащих акций. [c.271]
Нормальное распределение вероятностей (normal distribution) — наиболее широко используемое непрерывное распределение вероятностей, обычно имеющее вид колоколобразной кривой и полностью описываемое математическим ожиданием и дисперсией. [c.326]
В пределе получается непрерывное распределение вероятностей ( ontinuous probability distribution). Подобная кривая фактически изображает вершины многочисленных узких полос. (Технически кривая изображает то, что происходит, когда этих полос оказывается бесчисленное множество.) Рис. 6.6 приводит три примера такого рода кривых. Заметьте, что по вертикальной оси теперь измеряется плотность вероятности (вместо вероятности). [c.153]
По-видимому, самый распространенный прием заключается в том, чтобы выбрать наиболее вероятное значение. Его называют модой (mode) распределения вероятностей (для непрерывного распределения вероятностей мода есть результат с наивысшей плотностью вероятности). Рис. 6.6 показывает моду каждого из распределений. Отметьте, что на рис. 6.6(в) две моды в данном случае для ответа на заданный вопрос нельзя использовать ни одно отдельно взятое число. [c.156]
Крутизна кривой непрерывного распределения вероятностей ожидаемой доход ости менее рисковых активов более резко выражена, чем крутизна кривой для более рисковых активов. Какую форму приняла бы эта кривая в случаях а) безрисковых ак ривов и б) активов с абсолютно непредсказуемой доходностью [c.65]
На рис.10.3 показаны вычисленные вероятности в форме гистограммы. По оси у представлена шкала вероятностей и по оси х — интересующий нас параметр в данном случае — количество дней до момента доставки. Если соединить вершины каждого столбика (высота которых представляет вероятность доставок на соответствующий день после заказа), образуется агшроксимационная кривая, которую называют непрерывным распределением вероятностей. [c.152]
Сейчас мы разработаем метод поиска оптимального f по нормально распределенным данным. Как и формула Келли, это способ относится к параметрическим методам. Однако он намного мощнее, так как формула Келли отражает только два возможных результата события, а этот метод позволяет получить полный спектр результатов (при условии, что результаты нормально распределены). Удобство нормально распределенных результатов (кроме того факта, что в реальности они часто являются пределом многих других распределений) состоит в том, что их можно описать двумя параметрами. Формулы Келли дадут вам оптимальное f для бернуллиевых результатов, если известны два параметра отношение выигрыша к проигрышу и вероятность выигрыша. Метод расчета оптимального f, о котором мы сейчас расскажем, также требует только два параметра — среднее значение и стандартное отклонение результатов. Вспомним, что нормальное распределение является непрерывным распределением. Для того, чтобы использовать этот метод, необходимо дискретное распределение. Далее вспомним, что нормальное распределение является неограниченным распределением. Первые два шага, которые мы должны сделать для нахождения оптимального f по нормально распределенным данным, — это определить, (1) на сколько сигма от среднего значения мы усекаем распределение и (2) на сколько равноотстоящих точек данных мы разделим интервал между двумя крайними точками, найденными в (1). Например, мы знаем, что 99,73% всех точек данных находятся между плюс и [c.107]
В итоге мы получим взвешенное по вероятности HPR для каждого исхода. Возможен широкий диапазон результатов, но, к сожалению, эти результаты не непрерывны. Например, время до истечения срока не задается непрерывной функцией. До истечения срока всегда остается целое число то же верно и для цены базового инструмента. Если цена акции равна, например, 35, а минимальное изменение цены равно 1/8, то между 30 и 40 находится 81 возможное значение. Зная время, через которое мы собираемся продать опцион, можно рассчитать взвешенные по вероятности HPR для всех возможных цен на этот рыночный день. В нормальном распределении вероятности 99,73% всех результатов попадают в интервал трех стандартных отклонений от среднего, которое в нашем случае является текущей ценой базового инструмента. Поэтому нам необходимо рассчи- [c.166]
Распределения вероятностей бывают дискретными или непрерывными 2 Дискретное распределение вероятностей имеет конечное число исходов так, в табл 2.1 приведены дискретные распределения вероятностей Доходность казначейских векселей принимает только одно возможное значение, тогда как каждая из трех оставшихся альтернатив имеет пять возможных исходов Ка ждому исходу поставлена в соответствие вероятность его появления. Например, вероятность того, что казначейские векселя будут иметь доходность 8%, равна 1.00, а вероятность того, что доходность казначейских корпоративных облига ций составит 9%, ранна 0 50 [c.39]
Одним из видов непрерывного распределения, часто используемых в финансовых моделях, является равномерное распределение, при котором каждое значение моделиру емого показателя имеет одинаковую вероятность осуществления, т е. они равномерно распределены по всему интервалу изменения значений. На рнс. 2А.1 представлены два равномерных распределения Распределение А имеет диапазон изменения значений от — 5 до +15%- Следовательно, размах вариации составляет 20 единиц. Поскольку об щая площадь под функцией плотности должна равняться 1.00, высота распределения (Л) должна равняться 0.05 20Л = 1.0, т. е h — 0.05 С помощью этих данных можно найти вероятность появления различных результатов. Например, предположим, что не обходимо найти вероятность того, что доходность будет меньше нуля Вероятность пред ставляет собой площадь под функцией плотности от — 5 до 0%, т е заштрихованную площадь [c.70]
Другим полезным непрерывным распределением является треугольное рас пределение Этот тип распределения, представленный на рис. 2А.2, описывает ситуа цию, когда значения моделируемого показателя концентрируются около наиболее веро ятного среднего значения, причем вероятности появления значений, отклоняющихся от среднего, линейно уменьшаются с ростом этого отклонения. Диапазон значения доход ности распределения С — от —5 до +15%, а наиболее вероятное значение равно 10%. Наиболее вероятная доходность распределения D равна 5%, но диапазон ее значений составляет всего от 0 до +10%. Отметим, что распределение С сдвинуто влево, а распре деление D симметрично Ожидаемая доходность для распределения С составляет 6.67%, [c.70]
Смотреть страницы где упоминается термин Непрерывное распределение вероятностей
: [c.182] [c.182] [c.184] [c.326] [c.69] [c.77] [c.52] [c.536] [c.73]Смотреть главы в:
Количественные методы анализа хозяйственной деятельности -> Непрерывное распределение вероятностей
