Дисперсия характеризует степень разброса возможных результатов от наиболее вероятного значения по проекту. Дисперсия (а2 ) дискретного распределения рассчитывается по формуле [c.352]
Если бы мы записали точное время финиша, а не округленное до секунд, то могли бы построить непрерывное распределение. При непрерывном распределении нет ячеек. Представьте непрерывное распределение как серию бесконечно малых ячеек (см. рисунок 3-1). Непрерывное распределение отличается от дискретного, которое является ячеистым распределением. Хотя создание ячеек уменьшает информационное содержание распределения, в реальной жизни это единственно возможный подход для обработки ячеистых данных, поэтому на практике приходится жертвовать частью информации, сохраняя при этом профиль распределения. И наконец, вы должны понимать, что можно взять непрерывное распределение и сделать его дискретным путем создания ячеек, но невозможно дискретное распределение переделать в непрерывное. [c.83]
Сценарные спектры можно представлять себе как дискретные распределения. Такой же подход можно использовать и для определения вероятностей для непрерывного распределения, если рассматривать его как дискретное распределение с бесконечно малым шагом квантования (т. е. с бесконечным множеством сценариев). [c.164]
Используя непрерывные распределения вероятностей, аналитик может отказаться от точной оценки каждого результата в отдельности. Вместо этого аналитик должен прочертить кривую, которая отразит ситуацию так, как он ее видит. Относительная вероятность каждого отдельного результата (скажем, доходов в расчете на акцию 1,035) равна нулю. Однако относительная вероятность любого диапазона доходов определяется путем простого измерения площади между кривой и горизонтальной осью. Так, вероятность того, что доходы окажутся в пределах от 1,03 до 1,04, может быть установлена при измерении площади под кривой между 1,03 и 1,04, что в данном случае составит приблизительно 0,07 (т.е. 7 шансов из 100, что в следующем году доходы будут в пределах 1,03 — 1,04). Для дискретных распределений вероятностей наподобие тех, что показаны на рис. 6.4 и 6.5, ранее отмечалось, что сумма вероятностей должна равняться 1,0. И тогда при непрерывном распределении вероятностей общая площадь под кривой должна составить 1,0. [c.153]
Укажите, в чем различие между непрерывными и дискретными распределениями вероятностей. [c.165]
Напомним, что если число таких исходов конечно, то имеет место дискретное распределение вероятностей. В этом случае ожидаемую величину доходности можно представить в следующем виде [c.58]
Дисперсия и среднее квадратическое отклонение. Дисперсией, напомним, называется мера разброса возможных исходов относительно ожидаемого значения, причем чем выше дисперсия, тем больше разброс. Дисперсия дискретного распределения (а2) рассчитывается следующим образом [c.59]
При использовании сценарного подхода получают дискретное распределение вероятностей прогнозируемого показателя. [c.121]
Затем рассчитывается дисперсия дискретного распределения следующим образом [c.122]
При использовании сценарного подхода получают дискретное распределение вероятностей прогнозируемого показателя. Напомним, в этом случае ожидаемое значение показателя представляют в следующем виде [c.54]
Вы всегда принимаете решения на основе функции ожидаемой полезности. Для дискретных распределений доходов верно [c.57]
Современные автоматизированные производства являются примером сложных комплексов дискретных распределенных объектов управления, включающих основное обрабатывающее и вспомогательное технологическое [c.178]
Задачи контроля. Имеется система мониторинга, собирающая данные о состоянии комплекса дискретных распределенных объектов. Задана целе- [c.180]
Внутренняя организация системы и технология создания в ее среде конкретных прикладных систем основана на использовании методологии и моделей искусственного интеллекта. Базовой моделью является продукционная система с прямым выводом, которая была развита, расширена и переработана для описания и реализации процессов управления комплексами дискретных распределенных объектов в реальном времени. Настраиваемая база продукционной системы реального времени предназначена для хранения данных о динамике изменения состояний объектов и имеет прямой асинхронный информационный вход от внешних объектов и подсистем. Алгоритмы принятия решения и управления описываются на языке правил — продукций высокого уровня, допускающем квантификацию по объектам. Результатом продукционного логического вывода являются заключения о состоянии и ходе контролируемого процесса либо управляющие воздействия (команды) и сообщения, выдаваемые системой объектам по соответствующим каналам связи. Методы и внутренние формальные модели, положенные в основу реализации продукционной управляющей системы реального времени, демонстрируют следующие ключевые характеристики и особенности. [c.185]
Рассматривая теорию статистических оценок с позиций применения в массовых автоматизированных производствах, можно выявить две причины, существенно ограничивающие ее применение. Во-первых, точные результаты могут быть получены по результатам контроля большого числа партий, следовательно, информация о состоянии ТП поступит со значительными задержками во времени и не может быть использована для оперативного вмешательства в ход процесса. Во-вторых, статистический анализ состояния ТП базируется на исследовании погрешностей изготовления, подчиняющихся непрерывным распределениям (законам Гаусса, Максвелла, модуля разности и т. п.), а в основу теории несмещенных оценок положены дискретные распределения. Исходя из этого, можно сделать вывод о необходимости создания таких методов оценки результатов контроля, которые позволят избежать указанных недостатков. [c.12]
МЕТОД ДИСКРЕТНОГО РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ (ДЕРЕВА ВЕРОЯТНЫХ ИСХОДОВ) [c.235]
Таким образом, детерминированный эквивалент стохастической транспортной задачи с дискретно распределенным спросом может быть представлен следующей моделью линейного программирования [c.37]
По аналогии с приведенными моделями могут быть исследованы постановки стохастических транспортных задач, в которых случайными являются объемы производства аг = аг((о), и более общие модели, в которых не могут быть заранее предсказаны как объемы производства, так и спрос в пунктах потребления. Известны только статистические характеристики соответствующих случайных величин. Анализ всех этих. моделей сводится к решению задач выпуклого или линейного программирования в зависимости от того, имеем ли мы дело с непрерывно или дискретно распределенными случайными параметрами условий задачи. [c.38]
В [289] исследуются оптимальные смешанные стратегии детерминированной условной экстремальной задачи. Основной результат этой работы в том, что среди оптимальных решающих распределений задачи обязательно содержится дискретное распределение с не более чем т + 1 значениями составляющих решения (т — число ограничений). Как мы увидим далее, подобное утверждение справедливо для более широкого круга задач. [c.134]
Из формулы (ЗЛ9) видно, что в случае дискретного распределения случайного вектора Ь(ш) функции г(Хг), определяющие показатель качества двухэтапной задачи (3.15) — (3.18), являются кусочно-линейными функциями переменных v.i. Ввод дополнительных переменных и ограничений позволяет свести выпуклую кусочно-линейную задачу к задаче линейного программирования. [c.178]
В книге концентрируется внимание только на дискретных распределениях, по скольку они лучше иллюстрируют основные концепции риска и доходности. Однако непрерывные распределения также нашли широкое применение в финансовом анализе, поэтому они рассмотрены в Приложении 2А [c.39]
Рис 2 1 Графическое представление дискретного распределения вероятностей [c.40]
Дисперсией называется мера разброса возможных исходов относительно ожидаемого значения чем выше дисперсия, тем больше разброс Для расчета дисперсии дискретного распределения используется следующая формула [c.42]
| Рис. 2.5. Дискретное распределение (графики разброса). | 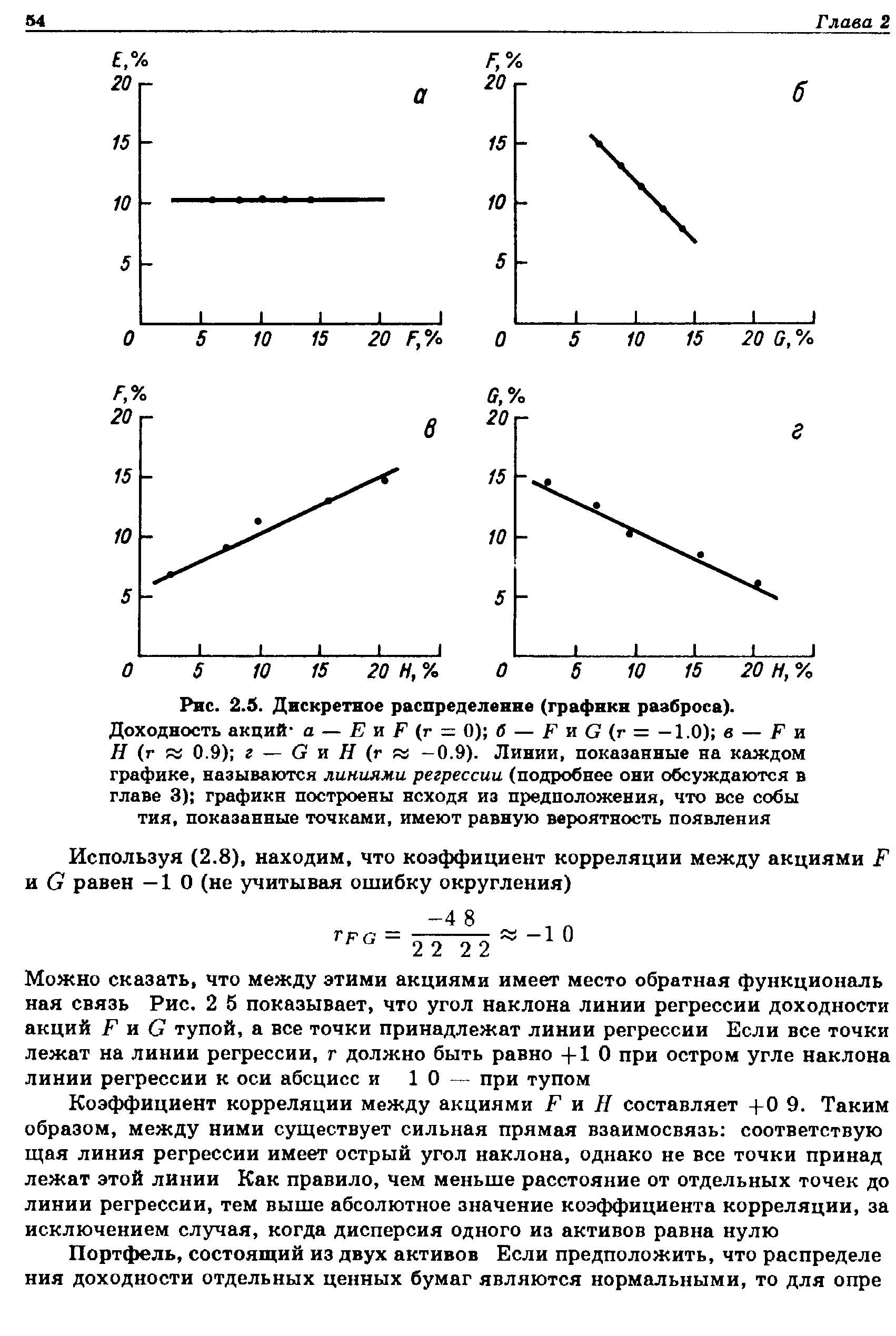 |
Оставшаяся часть этой главы посвящена анализу различных распределений вероятностей, применимых при оценке поведения рентабельности активов при условии соответствующих допущений. Начнем с двух непрерывных распределений — нормального и логнормального. Затем рассмотрим два дискретных распределения — биномиальное и Пуассона. Закончим рассмотрение группой других непрерывных распределений, в том числе и распределением Парето—Леви. Объясним наиболее желательные характеристики распределений с точки зрения финансового аналитика. [c.189]
Одним их наиболее важных дискретных распределений в финансах является биномиальное распределение. Для формирования биномиального распределения случайная переменная должна отвечать следующим четырем условиям. [c.200]
Определение издержек при эксплуатации объекта. Издержки при эксплуатации объекта направляются на выполнение технологических процессов, обеспечение действия инженерного оборудования зданий, поддержания в них нормативных санитарно-гигиенических условий и на содержание строительных конструкций в технически исправном состоянии. По периодичности выполнения их разделяют на две группы — дискретно распределенные по времени и непрерывно распределенные (текущие). К издержкам первой группы относятся годовые отчисления на полное восстановление и выполнение работ по капитальному ремонту (частичному восстановлению) основных фондов объекта (эти равномерно производимые начисления реализуются по времени неравномерно). Вторая группа — основные текущие годовые издержки Сэ при экплуатации промышленных зданий [c.183]
Для каждой реализации матрицы потоков = л /-/- в случае дискретно распределенной функции /(А) среднее количество частиц в f -м интервале вычислится по формуле [c.107]
Сейчас мы разработаем метод поиска оптимального f по нормально распределенным данным. Как и формула Келли, это способ относится к параметрическим методам. Однако он намного мощнее, так как формула Келли отражает только два возможных результата события, а этот метод позволяет получить полный спектр результатов (при условии, что результаты нормально распределены). Удобство нормально распределенных результатов (кроме того факта, что в реальности они часто являются пределом многих других распределений) состоит в том, что их можно описать двумя параметрами. Формулы Келли дадут вам оптимальное f для бернуллиевых результатов, если известны два параметра отношение выигрыша к проигрышу и вероятность выигрыша. Метод расчета оптимального f, о котором мы сейчас расскажем, также требует только два параметра — среднее значение и стандартное отклонение результатов. Вспомним, что нормальное распределение является непрерывным распределением. Для того, чтобы использовать этот метод, необходимо дискретное распределение. Далее вспомним, что нормальное распределение является неограниченным распределением. Первые два шага, которые мы должны сделать для нахождения оптимального f по нормально распределенным данным, — это определить, (1) на сколько сигма от среднего значения мы усекаем распределение и (2) на сколько равноотстоящих точек данных мы разделим интервал между двумя крайними точками, найденными в (1). Например, мы знаем, что 99,73% всех точек данных находятся между плюс и [c.107]
В третьей главе мы ознакомились с понятием изгиба цены опциона. Используя упрощенно-дискретное распределение, мы смогли увидеть, что этот изгиб возник благодаря тому, что к сроку истечения линия цены искривляется. Понятно, что, каковы бы ни были предположения о распределении цены акции, ценовой профиль всегда будет изогнут. А также каким бы ни было распределение, если волатильность высокая, то цена опциона должна направляться вдоль той кривой, что находится выше, и все утверждения, сделанные в четвертой главе по поводу влияния вола-тильности на дельту, гамму и тэту, остаются в силе. Модель Блэка-Шоул-за предполагает, что распределение основного инструмента логнормаль-ное. Вопрос о том, верно ли это предположение или нет, все еще является спорным. Эмпирические исследования показывают, что если изучаемый период не слишком длительный, то логнормальное распределение очень близко действительному процессу основного инструмента. Модель также предполагает, что ценовая волатильность акции постоянна, но чаще всего это совсем не так. Цены акции проходят как через волатильные, так и спокойные периоды. Некоторые исследования предполагают, что волатильность следует усредненно-оборотному процессу. То есть волатильность колеблется вокруг некоторой долгосрочной средней волатиль-ности. Итак, можно ли пользоваться моделью для торговли волатильностью или для оценки основного риска опционного портфеля Ответ поло- [c.193]
ДИСПЕРСИЯ [varian e] — характеристика рассеивания значений случайной величины, измеряемая квадратом их отклонений от среднего значения (обозначается 82). Различается Д. теоретического (непрерывного или дискретного) и эмпирического (также непрерывного и дискретного) распределений. Для наиболее часто применяемого в экономике эмпирического (дискретного) распределения Д. определяется по формуле [c.89]
Задачи управления комплексами дискретных распределенных объектов в реальном времени. Эти задачи являются наиболее функционально емкими и включают в себя задачи мониторинга, контроля и принятия решений. Наиболее простым развитием рассмотренных выше систем контроля, в том числе интеллектуальных, является управление компенсацией выявленных нежелательных отклонений от заданной идеальной целевой траектории системы в пространстве состояний. Необходимым дополнительным элементом здесь становится модель, описывающая структуру комплекса объектов, их свойства и среду функционирования, а также динамику их поведения. Такие модели должны содержать сложноструктурированный декларированный компонент, а описания процессов будут иметь вид логико-динамических моделей. В связи с этим процедуры обработки целесообразно строить как решающие процедуры определенных интеллектуальных систем. [c.181]
Коэффициент смещения (k- 1)/2л, полученный Г.П. Башариным для дискретных распределений, улучшает оценку энтропии непрерывного распределения. Предел точности измерений Ах (интервал группирования выборочных данных) позволяет свести дискретную величину к непрерывной, причем, чем меньше Ах, тем точнее выборочная энтропия описывает соответствующее теоретическое значение. [c.26]
Распределения вероятностей бывают дискретными или непрерывными 2 Дискретное распределение вероятностей имеет конечное число исходов так, в табл 2.1 приведены дискретные распределения вероятностей Доходность казначейских векселей принимает только одно возможное значение, тогда как каждая из трех оставшихся альтернатив имеет пять возможных исходов Ка ждому исходу поставлена в соответствие вероятность его появления. Например, вероятность того, что казначейские векселя будут иметь доходность 8%, равна 1.00, а вероятность того, что доходность казначейских корпоративных облига ций составит 9%, ранна 0 50 [c.39]
Дискретные распределения вероятностей могут быть представлены графи чески или в табличной форме На рис 2 1 приведены столбиковые диаграммы (или гистограммы) проектов 1 и 2 Возможные значения доходности проекта 1 принадлежат промежутку от —3.0 до +19.0%, а проекта 2 от —2.0 до +26.0% Отметим, что высота каждого столбца представляет собой вероятность появле ния соответствующего исхода, а сумма этих вероятностей по каждому вари анту равна 1.00. Отметим также, что распределение значений доходности про екта 2 симметрично, тогда как соответствующее распределение для проекта 1 имеет левостороннюю асимметрию. Аналогичные диаграммы для казначейских векселей и корпорационных облигаций показали бы, что доходность казначей ских векселей представлена единственным столбцом, а доходность корпорацион ных облигаций представлена диаграммой, имеющей правостороннюю асиммет рию [c.40]
Смотреть страницы где упоминается термин Дискретные распределения
: [c.17] [c.17] [c.18] [c.20] [c.22] [c.23] [c.26] [c.63] [c.185] [c.13] [c.70] [c.289] [c.180]Смотреть главы в:
Теория очередей и управление запасами -> Дискретные распределения
