Часть стоимости акции составляет приведенная стоимость дивидендов, на которые держатель опциона не имеет права. Поэтому, когда для оценки стоимости опциона "европейский колл" на акции, по которым выплачиваются дивиденды, вы используете модель Блэка-Шольца, вы должны уменьшить цену акций на приведенную стоимость дивидендов, выплачиваемых до срока исполнения опциона". [c.574]
Примечание. Основано на модели Блэка-Шольца. Для получения соответствующей стоимости европейского опциона "пут" прибавить приведенную стоимость цены исполнения и вычесть цену акции. [c.1038]
Биномиальная модель оценки стоимости опционов и модель Блэка-Шоулза. Их применение к оценке корпоративных облигаций и других условных требований [c.260]
Эта глава начинается с рассмотрения механизма заключения и исполнения опционных контрактов и того, как их можно использовать для создания различных схем денежных платежей на базе рискованных активов, лежащих в основе опционов. Далее мы используем закон единой цены для получения уравнений, увязывающих между собой цены опционов "колл", опционов "пут", акций и облигаций, а также рассмотрим биномиальную модель оценки стоимости опционов и модель Блэка—Шоулза. Затем будет показано, как по аналогии с опционами можно провести оценку стоимости облигаций и акций корпораций, воспользовавшись той же терминологией. В конце главы приведен обзор ряда приложений, для которых применима методика оценки условных требований. [c.260]
Рабочая книга Более реалистичная и часто используемая на практике модель оценки стоимости опционов на акции — это модель Блэка—Шоулза". При ее выводе используются соображения, аналогичные 15.7 описанным выше, однако при этом предполагается осуществление непрерывной корректировки дублирующего портфеля. [c.273]
Модель Блэка-Шольца предназначена для определения действительной стоимости опциона на основе цены базисной бумаги и ее волатильности, времени до срока истечения опциона и текущего уровня процентных ставок. При разработке модели ее авторы исходили из следующего [c.141]
Такая информация доступна в любое время по каждому опциону из его котировки, которая дает вам все, кроме подразумеваемой волатильности. Итак, какую волатильность вы должны подставить в модель Блэка-Шоулза (или любую другую используемую вами модель), чтобы получить из нее ответ 6 (текущую цену опциона) [c.213]
Текущая цена на первом шаге может пойти в 2-х направлениях. На втором шаге в 4-х направлениях. В биномиальной модели для расчета справедливой цены опциона вы должны заранее определить, сколько всего периодов использовать. Блэк-Шоулс считается предельной формой биномиальной модели, так как допускает бесконечное число периодов (в теории), то есть Блэк-Шоулс подразумевает, что эта небольшая диаграмма будет расширяться до бесконечности. Если вы определите справедливую цену опциона по Блэку-Шоулсу, то получите тот же ответ, что и в случае с биномиальной моделью, если число периодов, используемых в биномиальной модели, будет стремиться к бесконечности. (Тот факт, что Блэк-Шоулс является предельной формой биномиальной модели, подразумевает, что биномиальная модель появилась первой, но на самом деле сначала появилась именно модель Блэка-Шоулса). Справедливая стоимость фондового колл-опциона по Блэку-Шоулсу рассчитывается следующим образом [c.156]
Модель Блэка-Шоулса позволяет точно рассчитать дельту, то есть первую производную цены опциона. Это мгновенная скорость изменения опциона по отношению к изменению U (цены базового инструмента) [c.156]
С помощью этой формулы можно рассчитать HPR (взвешенное по вероятности результата) по сделке с опционом, при условии, что через время Т цена базового инструмента будет равна U. В данном уравнении переменная Т представляет собой долю года (выраженную десятичной дробью), оставшуюся до истечения срока опциона. Поэтому на дату истечения Т = 0. Если до истечения срока остается один год, то Т = 1. Переменная Z(T, U - Y) зависит от модели ценообразования, которую вы используете. Единственная переменная, которую вам надо рассчитать, — это Р(Т, U), т.е. вероятность того, что базовый инструмент будет равен U при заданном Т (т.е. времени, оставшемся до конца действия опциона). Если использовать модель Блэка-Шоулса или модель товарных опционов Блэка, то можно рассчитать Р(Т, U) следующим образом [c.166]
Так в чем же состоит эффективность применения этого другого распределения, отличающегося от нашего "наивного" нормального распределения Логнормальное распределение придает большую значимость текущей цене акции и меньшую значимость будущим ценам. Допущение меньшей вероятности экстремумов в распределении существенно уменьшает шансы возникновения большой стоимости опциона при истечении его срока и влияет на уменьшение ожидаемой стоимости. Но это, однако, компенсируется тем, что логнормальное распределение допускает вероятность очень экстремальных движений. На Рисунке 3.4 представлены кривые цен трехмесячного опциона колл, полученные при использовании "корректного" логнормального распределения, а именно модели Блэка-Шоулза, и нашего "наивного" нормального распределения. [c.50]
| Рисунок 3.4 Сравнение модели Блэка-Шоулза и "наивной" модели | 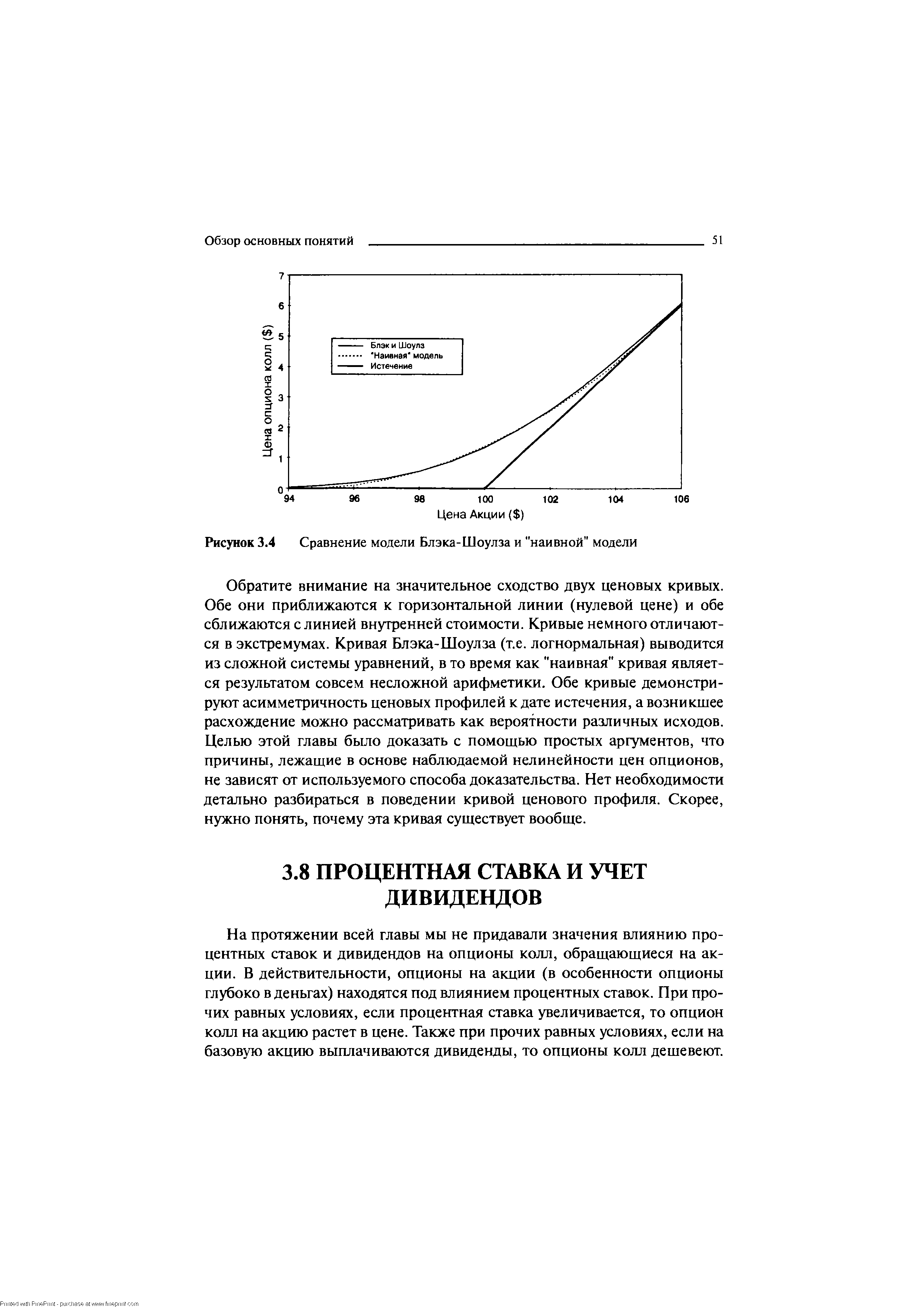 |
Теперь нам нужно подробно рассмотреть, каким образом меняется экспозиция по акции опциона колл. Весьма удобно, как для этой, так и для многих других экспозиций, рассматривать более долгосрочный опцион, поэтому Рисунок 3.6 показывает кривую цены одногодичного опциона колл с ценой исполнения 100. Для упрощения предположим, что мы имеем дело с ситуацией при нулевой процентной ставке, а опцион ведет себя полностью в соответствии с моделью Блэка-Шоулза. Этот опцион будет использоваться в качестве образца на протяжении всей четвертой главы, а подробный перечень цен будет представлен ниже. Однако здесь особое внимание нужно обратить на три точки кривой "А", "В" и "С". [c.52]
Для человеческого глаза профиль цены на Рисунке 3.7 кажется очень ровным. Переход от низко оцениваемых опционов к высоко оцениваемым опционам постепенный. Мы знаем, почему линия является кривой — из-за изгиба, или асимметрии, которая возникает при наступлении срока истечения. Но как насчет наклона (т.е. дельты) кривой Таким ли однородным является переход от нуля к единице Дельту опциона возможно рассчитать при каждом ценовом уровне акции. Дельта опциона также является инструментом модели Блэка-Шоулза и наряду с ценами опционов, большинство информационных служб свободно предоставляют расчеты значений дельты. На Рисунке 3.8 изображена кривая дельты рассматриваемого опциона, построенная по точкам различных уровней цены акции. [c.57]
Модель Блэка-Шоулза является сложным уравнением, требующим ввода определенной информации. Эта информация обычно используется в качестве параметров и для опционов на те акции, по которым дивиденды не оплачиваются. Они таковы (1) цена акции, (2) цена исполнения, (3) время до истечения срока, (4) процентная ставка (если это имеет значение в текущих обстоятельствах) и (5) волатильность цены акции. Как и во всех математических моделях, результирующие величины действительны только при условии, если введенная информация была правильной. Ошибка или неточность в исходной информации обязательно отразится на результате. Первые три переменные полностью и объективно оцениваемы, а четвертая, хотя и нефиксированная, как правило, довольно стабильна на протяжении всей жизни опциона. Волатильность не столь очевидна, и здесь необходимо прибегнуть к использованию исторической оценки или субъективного заключения. Если применяемое значение волатильности слишком высокое (низкое), тогда модель даст завышенную (заниженную) справедливую стоимость. Таблица 4.4 и Рисунок 4.6 показывают результаты использования различных данных по волатильности применительно к рассматриваемому одногодичному опциону колл. [c.81]
Мы могли бы пройти заново весь процесс, чтобы выявить линию цены опциона пут при наступлении срока истечения, но на самом деле в этом нет необходимости. Понятно, что результат будет очень похожим. Цена опциона пут к сроку истечения будет также изогнута, а этот изгиб возникает из-за скачка при наступлении срока. Кривая будет иметь другой вид, так как на этот раз нули присутствуют только при высоких ценах акции, а ненулевые значения при низких ценах. Модель Блэка-Шоулза помотает рассчитать цены опциона пут, которые приведены в Таблице 6.2 и отражены на Рисунке 6.2, где также показаны чувствительности для одногодичного опциона пут с ценой исполнения 100, основанные на предположении, как и в случае с колл опционом, что волатильность равна 15%. Для упрощения мы представим, что по акции не выплачиваются дивиденды и процентные ставки равны нулю. [c.128]
В Любом портфеле все отдельные опционы в большей или меньшей степени ведут себя согласно стандартной модели Блэка-Шоулза. Каждый компонент в разной степени вносит свою лепту во всеобщую экспозицию портфеля по акции положительную или отрицательную. Каждый компонент имеет различающуюся степень временного распада и различную чувствительность к рыночной волатильности. Управляющий таким портфелем должен следить за всеобщим влиянием разных компонентов и ему должна быть доступна оценка воздействия движений цен акций, влияния времени и изменения в волатильности. В этой главе мы покажем, каким образом можно оперировать более сложными опционными портфелями с использованием табличных процессоров. Однако некоторые из обычных опционных стратегий, включающие в себя простые комбинации, могут исследоваться с помощью несложных графических методов, и прежде чем мы рассмотрим более сложные варианты, обратимся к трем простым комбинациям. [c.154]
Одним из лучших примеров является японский рынок варрантов периода 1987 — 1993 годов. Японские варранты являются долгосрочными опционами колл, и по разным причинам они торговались с существенным дисконтом от теоретической стоимости, которая определялась по модели Блэка-Шоулза. В то время этому расхождению придумали удобное объяснение, согласившись с тем, что модель неприменима к опционам с четырьмя или пятью годами жизни. Основные участники рынка являлись спекулянтами, которые очень редко понимали теоретические стоимости, дельты и гаммы. Они просто покупали варрант, потому что рынок шел наверх. Ликвидность этих инструментов была огромна по сравнению с той, что наблюдалась на других рынках опционов, и часто можно было купить варранты стоимостью до 20 миллионов за один день. Большой спекулятивный интерес и отсутствие всякого значительного хеджирования предполагали возникновение бесчисленных аномалий и сохранение их на целые годы. Наиболее заметное неверное оценивание возникало тогда, когда варранты шли в деньгах. Спекулянты покупали варранты, очень далеко вне денег, по любой цене, тем самым поднимая подразумеваемую волатильность до 40%. Если им везло, а в конце 80-х им везло часто, цена основного инструмента росла, увеличивая цену варранта зачастую в пять или шесть раз от первоначальной стоимости. Обрадованные такими большими компенсациями за риск, спекулянты распродавали их частями, часто толкая цену от равноценных скидок к большим скидкам от теоретических стоимостей. Цены таких варрантов в деньгах были часто ниже тех цен, которые были получены на основе моделей, использовавших нулевое значение волатильности. Эти инструменты давали возможность хеджерам создавать длинные по волатильности портфели по отрицательной стоимости, а это означало, что даже в самом худшем случае при возникновении нулевой волатильности в результате все равно будет прибыль. И все это происходило, когда японский рынок ценных бумаг переживал один из самых волатильных периодов в своей истории. [c.196]
В приведенном выше примере одновременная покупка волатильности при 15% и продажа при 22%, скорее всего, приведет к прибыли, но что если подразумеваемые волатильности оказались ближе, скажем, 15% и 17% соответственно В таком случае, вероятнее всего, мы не сможем гарантировать прибыль. В большинстве случаев на биржевых опционных рынках можно найти такие опционы, которые обладают одинаковыми циклами истечения срока, обращаются на акции с различными ценами и имеют разные подразумеваемые волатильности. Первоначально многие профессионалы, наблюдающие эти различия, увеличивали хеджированные позиции, такие, как позиции, описанные выше. На ранних стадиях опционных биржевых рынков, когда аномалии были еще большими, многие из таких позиций приносили прибыль, но некоторые создавали убыток. Со временем протяженность аномалий сокращалась, но они все еще существовали. Некоторые профессионалы полагают, что модель неверна и что подразумеваемая волатильность не годится для измерения стоимости. Другие считают, что допущение логнормального распределения не является верным, и исследования в этой области все еще продолжаются. Однако некоторые ученые доказали, что аномалии могут быть объяснены, если отойти от предположения о постоянстве волатильности. Почти каждый согласится с тем, что изменяющаяся волатильность на некоторых рынках связана с ценой основного инструмента. Когда цена акции падает (растет), волатильность часто увеличивается (уменьшается). Было показано, что сочетание этих и других аспектов в модели Блэка-Шоулза совместимо с различными ценами акций, имеющих разные подразумеваемые волатильности. Поэтому модель все еще может быть использована, но при условии введения разных значений волатильности. Большинство участников рынка это и практикуют. [c.199]
Использование матрицы фиксированной или плавающей волатильности, как было описано выше, является попыткой рыночных профессионалов подогнать реальные цены опционов к тем, что даются моделью Блэка-Шоулза. Однако какова бы ни была ситуация, всегда можно прийти к волатильности, которая при вводе в модель Блэка-Шоулза дает цены, не противоречащие рынку. Но это не является обязательным, так как мы сами можем прийти к точному расчету чувствительностей опциона. Использование изменяющейся, или плавающей волатильности дает точные цены опционов, но не совсем точные дельты. [c.204]
С помощью сложных математических формул можно рассчитать обоснованную стоимость опциона. Лучшей из моделей оценивания европейских опционов считается модель Блэка-Шоулза. Для американских опционов применяется модель Кокса — Росса — Рубинштейна. Входными данными этих моделей являются текущая цена базового актива опциона, цена исполнения опциона, процентная ставка и количественная характеристика ценовой неустойчивости. На выходе модели формируется теоретическая стоимость опциона. Эти оценки используются затем биржевыми трейдерами, а также при окончательных расчетах по сделкам. [c.33]
Что такое модель Блэка-Шоулза [c.33]
Модель Блэка-Шоулза для опционов колл [c.658]
При решении задачи по данной формуле мы находим текущую цену акции, срок до окончания действия опциона, цену использования и краткосрочную ставку процента. Неизвестная переменная в таком случае — стандартное отклонение. Его следует вычислить. Стандартный подход — использование колебания прибыли по акциям за прошедшие периоды в качестве показателя на будущее. Блэк и Шолс так же, как и другие авторы, проверили модель, используя стандартные отклонения, оцененные по прошедшим периодам с определенной степенью успеха. Оценив равенство для опционов Блэк и Шолс получили соотношение акций и опционов, необходимое для поддержания полностью хеджированной позиции. В уравнении — это N(d ). Таким образом, модель Блэка—Шолса позволяет дать количественную оценку факторам, влияющим на стоимость опциона. Как мы видим, главным фактором является определение будущих колебаний акций. [c.665]
Модель цены опциона Блэка—Шолса дает точную формулу для определения стоимости опциона, основанную на изменчивости акций, ценах акций, цене использования опциона, времени до окончания срока его действия и краткосрочной ставке процента. Модель основана на предположении о том, что инвесторы способны поддерживать относительно хеджированные позиции во времени и что арбитражные сделки приведут прибыль на этой позиции к безрисковой ставке процента. В результате цена опциона имеет четкую взаимосвязь с целой акций. Модель Блэка— Шолса позволяет уяснить себе проблемы стоимостной оценки опционов. [c.666]
Примечание. Основано на модели Блэка—Шольиа. Вычесть 1,0 для получения соответствующих коэффициентов хеджирования для европейских опционов "пут". [c.1040]
Предположим, что курс акций может принимать при наступлении срока истечения опциона только одно из двух возможных значений. Несмотря на то что. такое предположение нереалистично, подобная двухступенчатая модель (лу/о-5Ы1е тоое ) создает основу для более реалистичной и широко используемой на практике биномиальной модели (Ьшопиа тоае ) оценки стоимости опционов. Интуитивное представление о стоимости опционов на основании двухступенчатой модели ведет также и к модели Блэка—Шоулза. [c.271]
Одним из основных допущений модели Блэка-Шоулза является предположение о случайном движении цен. Модель основывается на "гипотезе эффективного рынка", в соответствии с которой цены акций полностью отражают знания и ожидания инвесторов, поэтому trending sto ks не существуют (акции, движущиеся в одном направлении с основной тенденцией рынка, причем колебания их цен взаимосвязаны). Следовательно, бумаги с большими ценовыми колебаниями на рынке могут соседствовать с бумагами, показывающими высокую степень устойчивости. [c.20]
Историческая волатильность, безусловно, очень полезна в качестве исходных данных для опционной модели Блэка-Шоулза (или любой другой). Действительно, ввод волатштьности в любую модель чрезвычайно важен, поскольку эта компонента является существенным фактором определения цены опциона. Более того, историческая волатильность полезна не только для оценки цены опциона. Она также необходима для осуществления проектировок цены самой акции и расчетах распределений, что будет ниже. Каждый раз, когда вы задаете вопрос "Какова вероятность того, что акция двинется отсюда туда, или, что она превзойдет какой-либо целевой уровень ", ответ будет сильно зависеть от волатильности данной бумаги (или индекса, или фьючерса). [c.211]
Математически говоря, vega - это частная производная в модели Блэка-Шоулза (или любой другой модели, которую вы используете для оценки опциона) относительно волатильности. В вышеупомянутом примере, vega июльского 50 all-опциона, с ценой подлежащей акции XYZ в 50, вычисляется равной 0.098, очень близко к значению 0.10, к которому вы пришли ранее. [c.222]
Таким образом, в соответствии с моделью Блэка для фьючерсов справедливая стоимость колл-опциона с ценой исполнения 600, сроком исполнения 15 сентября 1991 года, при цене базового инструмента на 1 августа 1991 года 575, при вола-тильности 25%, с учетом 252-дневного года и R = 0 составляет 10,1202625. Интересно отметить связь между опционами и базовыми инструментами, используя вышеперечисленные модели ценообразования. Мы знаем, что 0 является наименьшей ценой опциона, но верхняя цена — это цена самого базового инструмента. Модели демонстрируют, что теоретическая справедливая цена опциона приближается к верхнему значению (стоимости базового инструмента U) при росте любой или всех трех переменных Т, R или V Это означает, что если мы, например, увеличим Т (время до срока истечения опциона) до бесконечно большого значения, тогда цена опциона будет равна цене базового инструмента. В этой связи мы можем сказать, что все базовые инструменты в действительности эквивалентны опционам с бесконечным Т. Таким образом, все сказанное верно не только для опционов, но и для базовых инструментов, как будто они являются опционами с бесконечным Т. Модель фондовых опционов Блэка-Шоулса и модель опционов на фьючерсы Блэка построены на определенных допущениях. Разработчики этих моделей исходили из трех утверждений. Несмотря на недостатки этих утверждений, предложенные модели все-таки довольно точны, и цены опционов будут стремиться к значениям, полученным из моделей. Первое из этих утверждений состоит в том, что опцион не может быть исполнен до истечения срока. Это приводит к недооценке опционов алгериканского типа, которые могут исполняться до истечения срока. Второе утверждение предполагает, что мы знаем будущую волатильность базового инструмента, и она будет оставаться постоянной в течение срока действия опциона. На самом деле это не так (т.е. волатильность изменится). Кроме того, распределение изменений волатильности логарифмически нормально, и эту проблему модели не учитывают1. Еще одно допущение модели состоит в том, что безрисковая процентная ставка остается постоянной в течение времени действия опциона. Это также не обязательно. Более того, краткосрочные ставки логарифмически нормально распределены. То обстоятельство, что, чем выше краткосрочные ставки, тем выше будут цены опционов, и утверждение относительно неизменности краткосрочных ставок может привести к еще большей недооценке опциона по отношению к ожидаемой цене (его правильному арифметическому математическому ожиданию). Еще одно утверждение (возможно наиболее важное), которое может привести к недооценке стоимости опциона, рассчитанной с помощью модели, по отношению к действительно ожидаемой стоимости, состоит в том, что логарифмы изменений цены распределяются нормально. Если бы опционы характеризовались не числом дней до даты истечения срока, а числом тиков вверх или вниз до истечения, а цена за один раз могла бы изменяться только на 1 тик и он был бы статистически независим от предыдущего тика, то мы могли бы допустить существование нормального распределения. В нашем случае логарифмы изменений цены не имеют таких характеристик. Тем не менее теоретические справедливые цены, полученные с помощью моделей, используются профессионалами на рынке. Даже если некоторые трейдеры применяют модели, которые отличаются от показанных здесь, большинство из них дадут похожие теоретические справедливые цены. Когда реальные цены расходятся с теоретическими до такой степени, что спекулянты могут получить прибыль, цены начинают снова сходиться к так называемой теоретической справедливой цене . Тот факт, что мы можем спрог-нозировать с [c.160]
Есть еще одна, заключительная деталь, объясняющая разницу между двумя подходами к определению справедливой стоимости. Скажем, мы точно знаем, что рассматриваемая акция будет демонстрировать волатильность 15% в обозримом будущем. Рассмотрим поведение двух участников рынка, покупающих одногодичный опцион колл и платящих правильную справедливую стоимость, рассчитанную с помощью модели Блэка-Шоулза при значении волатильности в 15%. Первый игрок следует стратегии покупки и удержания, а второй — дельта-нейтральной длинной стратегии на волатильность. Скажем, цена акции в самом начале равна 99, а цена исполнения — 100. Рассматриваемый опцион - тот, который мы изучали на протяжении этой главы, поэтому его цену мы уже знаем. Она составляет 5,46 или 546 за контракт. Оба игрока должны за длительный период времени оказаться безубыточными. Предположим, что цена акции к моменту истечения срока составляет 90. Первый игрок целиком потеряет всю свою ставку в 546, но игрок волатильностью возместит свои затраты в 546 за счет всей рехеджированной прибыли. Первый участник рынка потеряет 100% своей инвестиции, а второй достигнет уровня безубыточности. И оба заплатили правильную справедливую стоимость. Как такое может быть Представим, что обоим была дана вторая попытка при тех же самых инвестиционных стратегиях. Но на этот раз цена акции должна закончить свой путь, скажем на 114 и при этом опцион финиширует при стоимости в 14 или 1.400 за контракт. Первый игрок закончит с 1.400, в то время как второй закончит с 546. При второй попытке стратегия покупки и удержания принесет 1.400-546= 854, а [c.80]
При выявлении ценового профиля вышеописанной комбинации линии цен отдельных компонентов, имеющие значение для определения размеров позиций, были просто сложены друг с другом. Само по себе это утверждение вполне очевидно, но процедура эффективна только потому, что отдельные компоненты зависят от цены акции, лежащей в основе, а не друг от друга. (Для портфеля, содержащего различные акции, такая процедура не является приемлемой.). Понятие аддитивности (additivity) цены может быть применимо к большинству сложных портфелей, состоящих из большого количества разных позиций на опционы пут и колл. Однако когда количество разных позиций превышает число три, вышеуказанный графический метод не дает полного представления о стратегии. В конце концов, придется обратиться к компьютерной программе, которая смогла бы прочертить линию цены более сложных портфелей. В основе программы лежит модель Блэка-Шоулза. Мы делаем предположение о том, что цены модели и ценовая чувствительность в точности отражают то, что происходит на рынке. Для большинства рынков и в подавляющем числе случаев это предположение вполне допустимо. [c.165]
В третьей главе мы ознакомились с понятием изгиба цены опциона. Используя упрощенно-дискретное распределение, мы смогли увидеть, что этот изгиб возник благодаря тому, что к сроку истечения линия цены искривляется. Понятно, что, каковы бы ни были предположения о распределении цены акции, ценовой профиль всегда будет изогнут. А также каким бы ни было распределение, если волатильность высокая, то цена опциона должна направляться вдоль той кривой, что находится выше, и все утверждения, сделанные в четвертой главе по поводу влияния вола-тильности на дельту, гамму и тэту, остаются в силе. Модель Блэка-Шоул-за предполагает, что распределение основного инструмента логнормаль-ное. Вопрос о том, верно ли это предположение или нет, все еще является спорным. Эмпирические исследования показывают, что если изучаемый период не слишком длительный, то логнормальное распределение очень близко действительному процессу основного инструмента. Модель также предполагает, что ценовая волатильность акции постоянна, но чаще всего это совсем не так. Цены акции проходят как через волатильные, так и спокойные периоды. Некоторые исследования предполагают, что волатильность следует усредненно-оборотному процессу. То есть волатильность колеблется вокруг некоторой долгосрочной средней волатиль-ности. Итак, можно ли пользоваться моделью для торговли волатильностью или для оценки основного риска опционного портфеля Ответ поло- [c.193]
Как это ни странно, многие категории участников рынка, такие как, например, маркет-мэйкеры, занимающиеся покупкой и продажей варрантов и не придающие абсолютно никакого значения таким сложным моделям, очень хорошо улавливают реальные чувствительности цен варрантов и, устанавливают хеджи, используя верные эмпирические дельты (empiri al deltas). Они зарабатывают огромную прибыль, на самом деле не зная даже почему. По прошествии времени умудренные опытом хеджеры все больше и больше втягиваются в рынок и для расчета дельт предпочитают использовать эмпирический статистический анализ вместо модели Блэка-Шоулза. Конечным результатом этого хеджирования оказывается, к сожалению, исчезновение аномалий. Японские варранты теперь торгуются по ценам, очень близким к тем, что дает модель. [c.197]
Формулы оценки опционов. Опционы на акции, подаренные служащим компании или еще кому-то, теоретически влекут те же последствия, что и варранты, о которых мы говорили выше, но у этих опционов нет рыночной цены. Их рыночную цену можно подсчитать с помощью модели Блэка—Шольца или использовать какую-либо из ее модификаций3, или использовать модель минимальной стоимости. Это даст аналитику возможность прикинуть, насколько стоимость опциона превосходит цену исполнения. Это помогает оценить вероятность исполнения, поскольку надбавка над ценой исполнения препятствует исполнению. [c.366]
Еще одним феноменом в этой области является рост волатильности цен на рынке акций, отмечаемый и анализируемый в последние годы (в качестве убедительной иллюстрации можно, к примеру, обратиться к Табл. 5), а причиной этого явления чаще всего называется популярность стратегий хеджирования с помощью производных инструментов. И действительно, исследования показывают, что оптимальные стратегии хеджирования (с использованием усовершенствованной знаменитой модели Блэка-Шоулза) не только обеспечивают положительную обратную связь с ценами, но и увеличивают волатильность цен [381]. Как отмечал Миллер (Miller) [298], в финансовой прессе практически ежедневно звучит следующее, широко распространившееся мнение рост волатильности рынка акций в последнее десятилетие происходил в основном благодаря появлению на рынке дешевых спекулятивных инструментов, таких как фьючерсы на фондовые индексы и опционы. Однако, было бы наивно объяснять рост волатильности только этой [c.99]
Смотреть страницы где упоминается термин Модель Блэка
: [c.582] [c.260] [c.285] [c.285] [c.348] [c.20] [c.31] [c.141] [c.167] [c.50] [c.128] [c.658]Смотреть главы в:
Экономические и финансовые риски Оценка, управление, портфель инвестиций -> Модель Блэка
