Равномерный закон распределения 34 Размер матрицы 2 Размерность пространства 270 Ранг 78 [c.304]
В некоторых случаях известно заранее, что результат измерения подчиняется равномерному закону распределения вероятности. Например, из-за люфтов и трения в опорах подвижной части измерительного механизма он с равной вероятностью может отличаться от среднего значения на любую величину в пределах общего люфта. Последний обычно известен, так что появление больших отклонений может быть следствием только ошибок. Без дополнительной проверки они должны быть отброшены. [c.79]
Такой вариант встречается при люфте подвижной части измерительного механизма. Результат измерения Q подчиняется равномерному закону распределения вероятности с тем же размахом е, но смещенному по отношению к закону распределения вероятности показания на значение поправки 0,-, внесением которой обеспечивается правильность измерения. Значение измеряемой величины Q, равное среднему значению результата измерения Q, находится в пределах [c.86]
Ситуационной моделью, учитывающей неопределенность значения поправки, является равномерный закон распределения вероятности 9 на интервале от min ДО тах. Закон распределения вероятности результата измерения Q представляет собой композицию законов распределения вероятности показания и ситуационной модели. Композиция, в которую входит ситуационная модель, не подчиняется вероятностно-статистическим закономерностям. Однако по аналогии с вариантом 1 в 1981 году Международным комитетом мер и весов рекомендовано считать, что с высокой вероятностью среднее значение композиции, равное значению измеряемой величины, не отличается от результата однократного измерения, больше чем на е = kug, где UQ = - а. + н а коэффициент k, аналогичный коэффициенту t, устанавливается по соглашению. Обычно он принимается равным 2. .. 3. [c.88]
Пользуясь методом характеристических функций, можно показать, что композицией одинаковых равномерных законов распределения вероятности, которым подчиняются два независимых результата измерений, является треугольный закон (рис. 61), называемый законом распределения вероятности Симпсона. Композицией двух равномерных законов распределения вероятности независимых результатов измерений с неодинаковым [c.155]
Чему равна масса каждой гири в интервале от 1,99 кг до 2,01 кг неизвестно. Представим и эту ситуацию математической моделью в виде равномерного закона распределения вероятности на интервале от 1,99 кг до 2,01 кг со средним значением и аналогом дисперсии [c.156]
Пример 40. Найти плотность распределения вероятности суммы двух независимых результатов измерений А ч В, первый из которых подчиняется нормированному нормальному закону, а второй - равномерному закону распределения вероятности на интервале (-1,1). [c.159]
Число каналов сервера 2, имитирующего процессор, равно единице, поэтому процессор одновременно обрабатывает один процесс (запрос). Время обслуживания - это время обработки ветви программы процесса между двумя прерываниями оно имеет равномерный закон распределения. [c.315]
Базовой последовательностью случайных чисел, используемой для формирования в ЭВМ случайных элементов различной природы, с различными законами распределения является совокупность случайных чисел с равномерным законом распределения [c.199]
Получение псевдослучайных чисел с равномерным законом распределения заключается в выработке псевдослучайных чисел. Псевдослучайные числа - это числа, полученные по какой-либо формуле и имитирующие значения случайной величины. Под словом имитирующие подразумевается, что эти числа удовлетворяют ряду тестов так, как если бы они были значениями этой случайной величины. [c.122]
Существует основное соотношение, связывающее случайные числа с заданным законом распределения и случайные числа с равномерным законом распределения в интервале [0,1]. Суть его состоит в том, что для преобразования последовательности случайных чисел с равномерным законом распределения в интервале [0,1] в последовательность случайных чисел с заданной функцией рас- [c.122]
С помощью критерия х,2 можно проверять не только гипотезу о согласии эмпирического распределения с нормальным законом, но и с любым другим известным законом распределения - равномерным распределением, распределением Пуассона и т. д. Например, суд рассматривает жалобу посетителей казино на то, что, по их мнению, игральная кость, которой там пользуются, фальшива, некоторые числа очков, якобы, выпадают чаще, чем другие, и этим пользуются крупье, обирающие игроков. [c.201]
В процессе реализации метода Монте-Карло производится моделирование случайных событий и соответствующих им случайных величин. При таком моделировании определяется, произошло или не произошло в данном испытании некоторое событие А, вероятность которого известна и равна Р(А), и устанавливается, какое значение приняла соответствующая случайная величина X, закон распределения которой известен. С этой целью решают вспомогательную задачу, состоящую в моделировании равномерно распределенной в интервале (0,1) случайной величины со, Пусть, например, известна вероятность некоторого события А [c.154]
Моделирование количества продуктивных пластов производится исходя из известной статистики по открытым в районе месторождениям (с использованием нормального закона распределения с математическим ожиданием и дисперсией, определяемыми из статистики). При реализации модели в нашем случае был использован упрощенный подход из реальной статистики количества продуктивных пластов в районе на каждом шаге имитации с равной вероятностью выбиралось количество продуктивных пластов. При более точном подходе необходимо -брать значения соответствующих геологических параметров в равномерно распределенных по площади района точках исходя из прогнозных карт. [c.203]
Встроенный в компьютер генератор псевдослучайных чисел выдает числа, равномерно распределенные в интервале от 0 до 1. Так как любая интегральная функция распределения F(x) имеет область значений от 0 до 1, то с помощью равномерного распределения можно получить случайное число с произвольным законом распределения путем решения обратной задачи, то есть восстанавливая по известному значению F(x) значение х. В качестве примера будем моделировать случайную величину, подчиняющуюся обобщенному экспоненциальному [c.48]
Реализация и опытная апробация постановки и метода решения задачи. Разработанный метод и весь комплекс связанных алгоритмов и процедур реализованы в комплексе программ на языке ФОРТРАН-IV для ЕС ЭВМ [97]. С использованием этого комплекса проведены многовариантные расчеты для задач перспективного планирования развития ЕГС и системы газоснабжения Северо-Западного экономического района. При этом в рамках ЕГС учитывалось 25 месторождений газа (или пунктов поставки в систему попутного газа), 102 пункта потребления газа, 251 участок магистральных газопроводов. Для каждого случайного параметра принят равномерный закон вероятностного распределения. [c.153]
Наиболее простым законом распределения случайных величин является закон равномерной плотности непрерывной величины, согласно которому все значения случайной величины в пределах определенного интервала одинаково вероятны. Функция распределения этой величины представлена на рис. 33, где С — некоторая постоянная величина. [c.133]
Для исследований базисной устойчивости стохастической транспортной задачи может быть использован метод статистических испытаний (метод Монте-Карло) в сочетании с двойственным методом потенциалов. При этом данные, характеризующие ресурсы поставщиков и потребности потребителей, формируются ЭВМ на основе определенных законов распределения и возможных интервалов их изменений. Под набором подразумевается совокупность величин ресурсов и потребностей, которые соответствуют их предполагаемым значениям в заранее определенных интервалах. Необходимое число наборов значений ресурсов и потребностей формируется соответствующей машинной программой для ЭВМ Минск-22 . При этом по рекуррентному соотношению по способу перемешивания определяется последовательность квазислучайных чисел, обладающих статистическими свойствами последовательности независимо от выбранных значений равномерно распределенной случайной величины =f (l/z-i),l г /г ЛЛ Полученные числа обычно удовлетворяют системе принятых статистических критериев для проверки равномерности распределения. [c.112]
Аналогичным порядком могут быть получены выражения для Pan и Р3п при других законах распределения q, t2, t3. Так, при равномерном рас- [c.119]
Если какие-либо значения Q более вероятны, чем другие, это Должно быть принято во внимание. Тогда подбирается соответствующий закон распределения вероятности Q на интервале возможных значений. Если же на этом интервале Q с одинаковой вероятностью может иметь любое значение, то закон распределения вероятности Q принимается равномерным. [c.72]
Рие. 24. Центрированный закон равномерной плотности распределения вероятности [c.73]
| Рис. 63. График плотности распределения вероятности (3) композиции нормированного нормального (1) и равномерного (2) законов распределения | 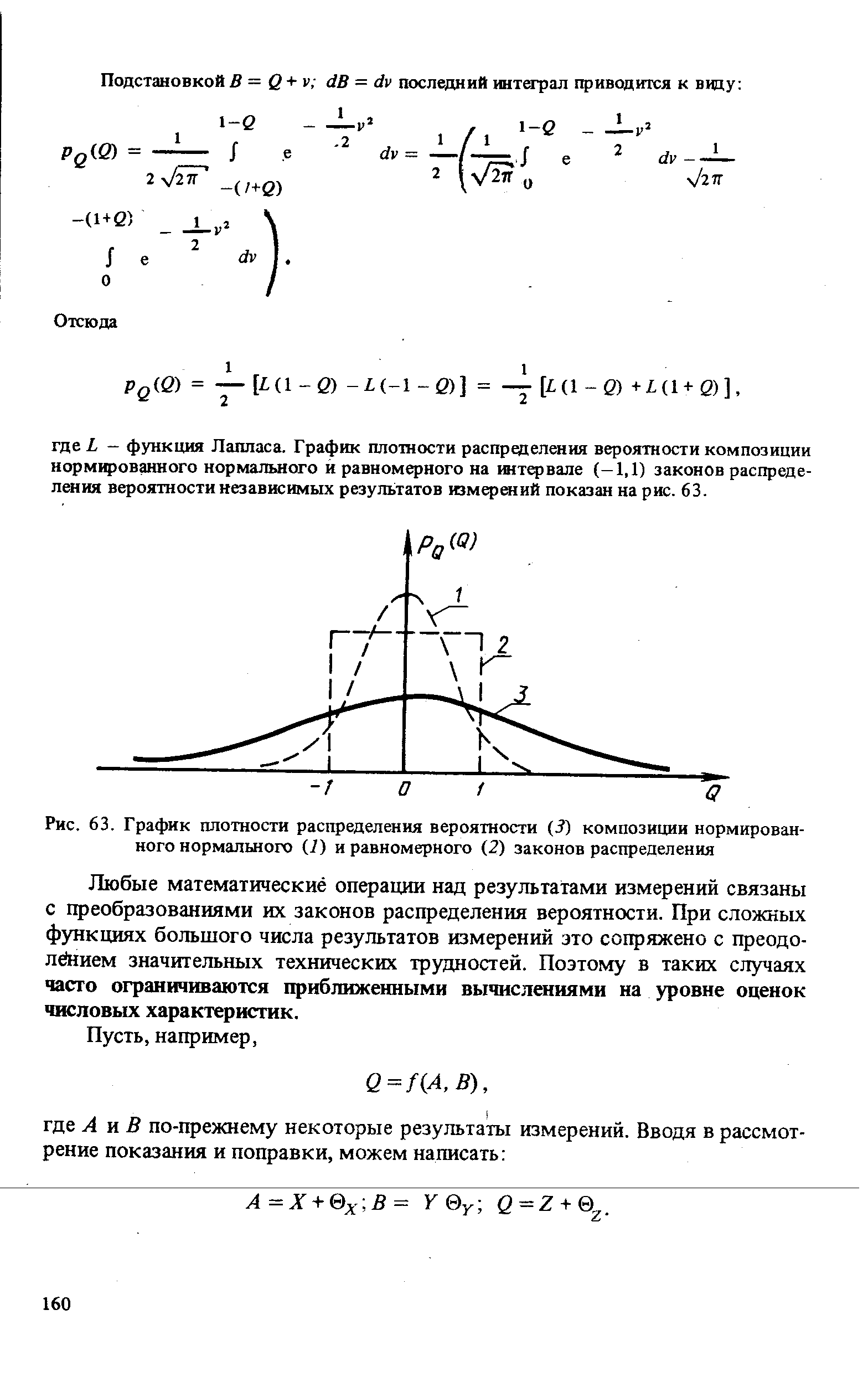 |
Рассмотрим задачу определения потерь от случайной составляющей погрешности измерений. Для этого воспользуемся выражением (1.4.20) и двумя способами нормирования случайной составляющей погрешности пределом допускаемого значения средним квадратическим отклонением. При этом примем во внимание три наиболее распространенных закона распределения погрешности нормальный, треугольный и равномерный. Результаты расчетов функции потерь от погрешности измерений Пнх, проведенных по формуле (1.4.20), представлены в табл. 3.3.1. [c.121]
Снижение налогового бремени невозможно осуществить, не добившись равномерного его распределения среди налогоплательщиков. Одним из основных инструментов, призванных обеспечить равномерность распределения налогового бремени, является Федеральный закон от 31 июля 1998 г. № 148-ФЗ О едином налоге на вмененный доход для определенных видов деятельности . Данный Закон направлен на привлечение к уплате единого налога на вмененный доход организаций и индивидуальных предпринимателей, занимающихся предпринимательской деятельностью в сферах, где налоговый контроль значительно затруднен, а именно в розничной торговле, общественном питании, бытовом и транспортном обслуживания. У них значительная часть расчетов с покупателями и заказчиками осуществляется в наличной денежной форме. [c.8]
Поскольку нам ничего не известно о законах распределения погрешностей измерений Дд-, Ду, Д , то единственно, что мы можем сделать, это, абстрагируясь от заданных вероятностей Р%, Ру, Pz принять равномерные распределения погрешностей в пределах указанных интервалов А , Ay,,- Zp (можно было бы ввести соответствующие поправки на хвосты" распределений, однако, учитывая достаточно высокий уровень значений вероятностей Р%, Ру, Р%, можно заранее предположить несущественность этих поправок). [c.73]
Во-первых, необходимо решить, какие принять законы распределения Дт и Дк. Что касается погрешности Д, то, поскольку задан лишь класс точности средства контроля, закон ее распределения может быть принят равномерным в пределах от — 0,1 до + 0,1 кОм, т.е. Дкр =0,1 кОм. [c.163]
Аналогичные таблицы для равномерного и других законов распределения погрешностей приведены в МИ 188 — 79. [c.170]
Отмеченное позволяет ввести понятие о некой обобщенной характеристике точности измерений (и средств измерений) — энтропийной погрешности. При этом энтропийной погрешностью считается погрешность с равномерным распределением, которая вносит такое же дезинформационное действие (обеспечивает такую же остаточную неопределенность), что и погрешность с данным (реальным) законом распределения. [c.244]
Модификацией теории предельной полезности, получившей развитие в 20 в. в Великобритании, США и др. странах явилась теория предельной производительности факторов произ-ва, отрицающая создание прибавочной стоимости трудом (см. Маржинализм, Производительности теория). На основе предельной полезности выдвигается т. н. теория благосостояния. Часть сё сторонников из числа радикальных экономистов, исходя из постулата убывающей ценности доходов, выдвигает требование более равномерного их распределения с помощью соответствующей налоговой системы. В результате этого, по их мнению, даже без увеличения общей суммы доходов должна повыситься их совокупная ценность. Однако ортодоксальные последователи А. ш. Л. Мизес, Ф. Хайек (США) и др. относят закон убывающей ценности только к благам, а не к доходам и отвергают перераспределение доходов, ущемляющее интересы капиталистич. класса. [c.14]
Вероятность, с которой случайная величина (а размер ошибки — случайная величина) принимает конкретное числовое значение, связана с численным значением случайной величины своим законом распределения. Распределения, как известно, бывают разные (равномерное, биномиальное, показательное, нормальное, хи-квадрат и т. д.). В силу изложенного в п. 3.4 есть все основания полагать (и литературные данные подтверждают это), что размер ошибки распределен по [c.116]
Практически при k > 15 обеспечивается требуемая точность в имитационных исследованиях. Поэтому в дальнейшем будем говорить о равномерном законе, хотя в действительности при программном моделировании имеем дело с квазиравномерным законом. При выводе выражений (9.2) предполагалось, что х формируется на основе случайных чисел о,, принимающих значения (0 1) с вероятностью PJ = 1/2, для чего в машине должен существовать случайный генератор, дающий строго случайные последовательности чисел о, с соответствующим распределением. Так как в ЭВМ такого генератора нет, случайные числа вырабатываются программным путем, в силу чего они, строго говоря, не являются случайными, так как формируются на основе вполне детерминированных преобразований, поэтому их называют псевдослучайными. Такие последовательности случайных чисел являются периодическими, поэтому очень длинные последовательности, длина которых превосходит период, уже не будут строго случайными. - [c.200]
Вариант 2. Априорная информация отсчет, а следовательно и показание подчиняются равномерному закону распределения вероятности с размахом е = Хтах — X точное значение аддитивной поправки равно 0, [c.86]
| Рис. 61. Равномерная плотность распределения вероятности результата измерения (7) и плотность распределения вероятности композиции двух (2) и трех (3) таких законов распределения вероятности (а - при Q = 0 б - при Q = 0,5) размахом является трапецеидальный закон. Это обстоятельство часто используется при учете дефицита информации. Рассматривая произведение большого числа характеристических функций, можно убедиться в том, что независимо от пида сомножителей оно стремится к характеристической функции, соответствующей нормальному закону распределения вероятности. Это фундаментальное положение носит название центральной предельной теоремы. На рис. 61 видно, как быстро нормализуется композиция одинаковых равномерных законов распределения вероятности. При числе слагаемых больше 4-х уже можно считать, что она практически подчиняется нормальному закону. | 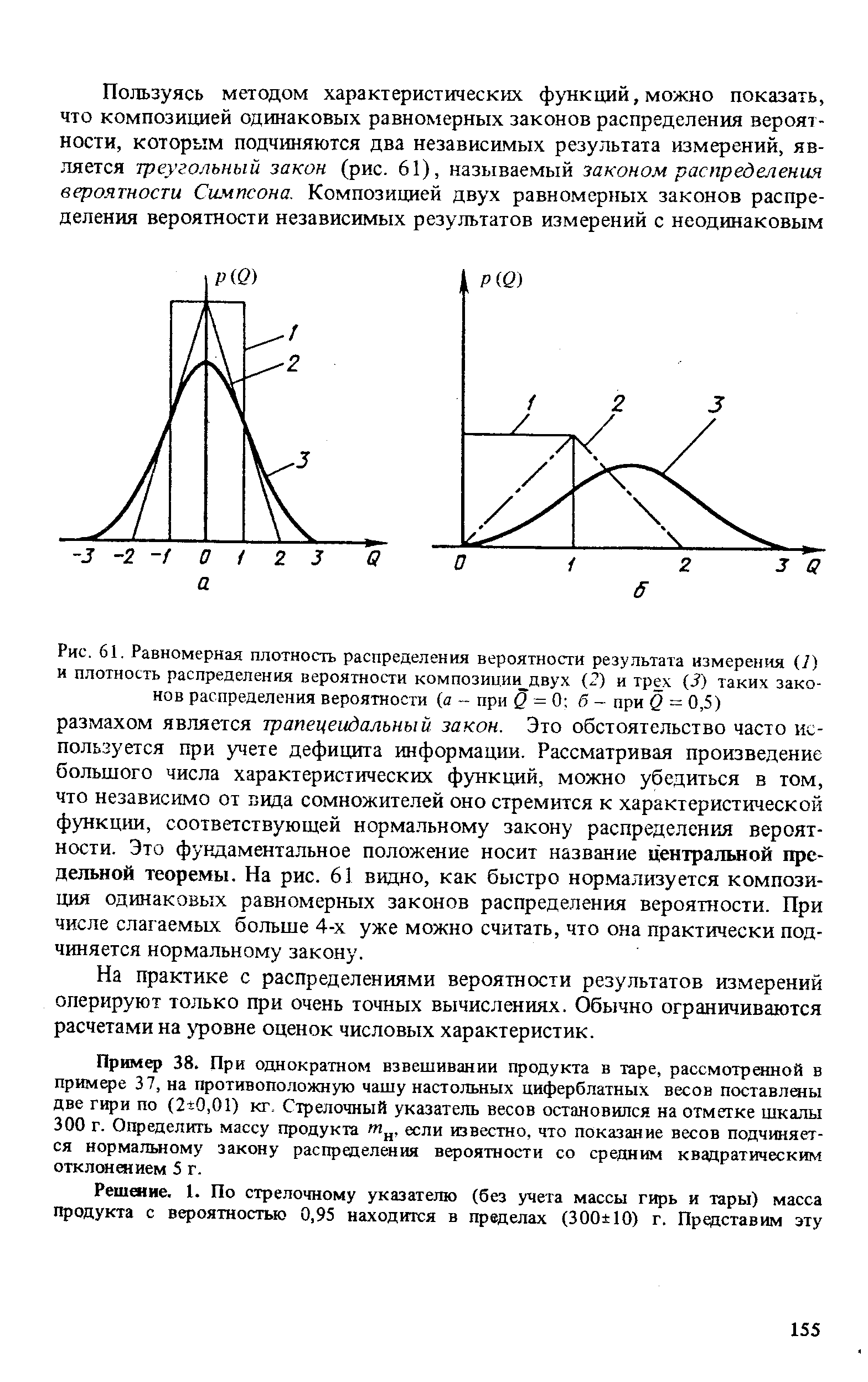 |
Относительно процесса возрождения Европы план Маршалла предполагал временное приостановление действия принципов экономического либерализма. Программа, рассчитанная на четыре года, должна была помочь Европе добиться реальной независимости. Предполагалось сосредоточиться на выполнении следующих задач модернизации инфраструктуры, увеличения объемов производства (в частности, в ключевых отраслях - металлургии и энергетике), более равномерному географическому распределению тяжелой индустрии, сконцентрированной для этого в зоне Рура, рационализации производства в сельском хозяйстве и легкой промышленности и, наконец, денежной и финансовой стабилизации. По прошествии четырех лет предусматривалось полное восстановление принципов экономического либерализма. США приняли самое активное участие в реализации этой программы. К услугам европейских стран были американский экономический опыт и профессиональные эксперты. Но гораздо более важную роль играло оказание огромной финансовой помощи. Существовавшие и будущие дефициты платежных балансов европейских государств были частично покрыты долгосрочными займами Мирового банка, основным вкладчиком капитала которого были США. Долги достигли 3 млрд долл. Остаток, куда более важная часть, был погашен США в виде финансовой помощи. Трумэн предложил конгрессу предоставить Европе помощь на сумму в 20 млрд долл. в рамках Закона об экономическом сотрудничестве (E onomi ooperation A t) в итоге он составил 17 млрд долл.12 [c.229]
Другим широко используемым законом распределения погрешностей является закон равномерной плотности. Характерная особенность равномерного распределения состоит в том, что появление (при данном распределении) любого значения погрешности в интервале ее возможных значений (от Дт1п до Дтах) может произойти с одинаковой вероятностью. [c.54]
Равномерное распределение, как правило, использу когда заданы лишь границы допускаемых значений вестно действительное распределение погрешности в предел ч и требуется определить ее среднее квадратическое отклонеян 1. ливается тем, что оценка среднего квадратического отклонен ти в предположении равномерного распределения имеет мако сравнению с другими законами распределения) значение, т.е. мы платим точностным запасом. [c.55]
В других случаях этот выигрыш" может быть большим или меньшим, но он всегда есть. Это обусловливается тем, что при использовании М [Д05 ], а [Д ] (см. формулу (3.7) для расчета Д0 не требуется знания закона распределения Д05. При использовании же для расчетов Д0 нормированного значения Д05р (см. формулу (3.8) желательно знать закон распределения Д08, но мы его не знаем (в технической документации на средства измерений такие данные не приводятся) и вследствие этого вынуждены полагать закон распределения Д05 в пределах нормированных значений Д08р равномерным, что, как правило, приводит к завышенным расчетным оценкам интервалов для Д0. [c.134]
При отсутствии каких-либо данных о реальном распределении значений Дт и для них может быть принято равномерное распределение (дающее некоторый точностной запас по сравнению с расчетами, выполненными для других законов распределения). [c.163]
