Показатель эксцесса (Е) и его ошибка (те) рассчитываются следующим образом [c.143]
| Рис. 5.3. Асимметрия распределения Показатель эксцесса рассчитывается по формуле | 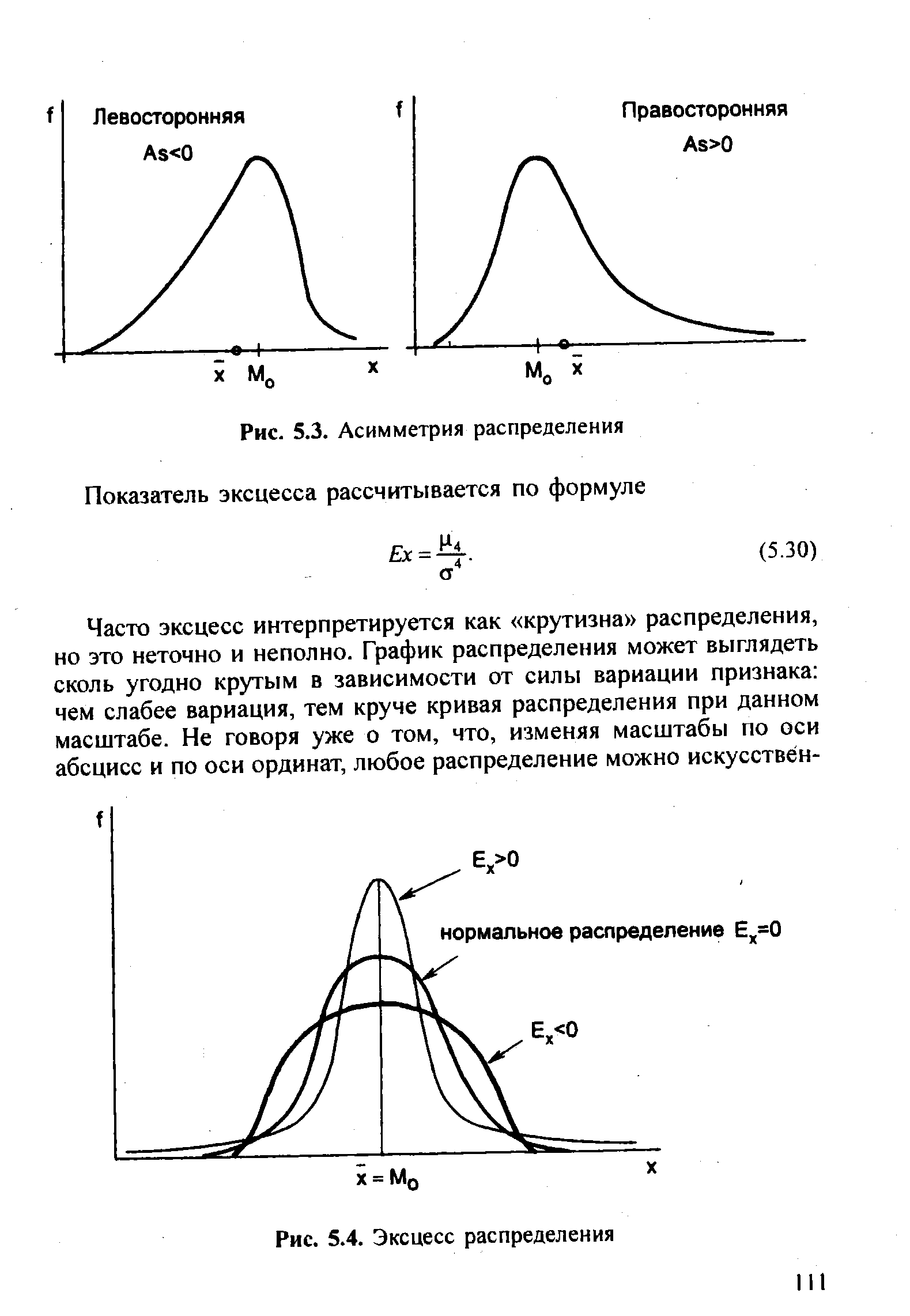 |
Однако такой показатель не следует называть термином эксцесс , что в переводе означает излишество . Термин эксцесс следует применять не к самому отношению по формуле (5.30), а к сравнению такого отношения для изучаемого распределения с величиной данного отношения нормального распределения, т.е. с величиной 3. Отсюда окончательные формулы показателя эксцесса, т.е. излишества в сравнении с нормальным распределением при той же силе вариации, имеют вид [c.112]
Зная среднюю величину изменения показателя и индивидуальные индексы, можно проводить анализ методами вариационной статистики анализировать распределение товаров по изменению цен, объема покупок, сравнивать модальное и среднее изменение, максимальное и минимальное по показателям эксцесса распределений делать выводы о том, насколько однородны изменения цен и количества по отдельным товарам, группировать товары по уровню цен и степени их изменения и т. д. [c.379]
Крутизна распределения данных, или степень выпуклости его вершины, характеризуется показателем эксцесса [c.120]
Для нормального распределения Ех = 0. Большой положительный эксцесс означает, что в совокупности данных есть слабо варьирующее по данному признаку ядро , окруженное редкими, сильно отстоящими от него значениями. Большое отрицательное значение показателя эксцесса свидетельствует об отсутствии такого ядра . [c.120]
Показатель асимметрии 0,50263 Показатель эксцесса —0,29715 —01 [c.222]
Показатель асимметрии 0,52392 —01 Показатель эксцесса 1,2619 [c.224]
Показатель асимметрии 0,13040/ —01 Показатель эксцесса —0,15626 [c.225]
Крутизна распределения данных характеризуется показателем эксцесса [c.89]
Число единиц в выборке, N Величина интервала, Н Показатель асимметрии ряда, гл Показатель эксцесса, Ех Дисперсия, а Среднее значение, X Критерий согласия, К [c.81]
Для представления обобщающих показателей, предположим, доходности активов, цен активов или числа финансовых операций, мы используем показатели центра распределения, показатели вариации, показатели скошенности (асимметрии) и показатели эксцесса. [c.77]
В то время как показатели асимметрии характеризуют симметричность распределения частот, показатели эксцесса описывают [c.94]
В нормальном распределении показатель эксцесса Е = 0. Если Е > 0, то данные густо сгруппированы около средней, [c.140]
Следующее требование к исходной информации — подчинение ее закону нормального распределения. Для количественной оценки степени отклонения информации от нормального распределения служат отношение показателя асимметрии к ее ошибке и отношение показателя эксцесса к его ошибке. [c.40]
По значениям показателей асимметрии и эксцесса распределения можно судить о близости распределения к нормальному, что бывает существенно важно для оценки результатов корреляционного и регрессионного анализа, возможностей вероятностной оценки прогнозов (см. главы 7,8,9). Распределение можно считать нормальным, а точнее говоря - не отвергать гипотезу о сходстве фактичес- [c.112]
Если же с изменением значения признака х среднее значение признака у не изменяется закономерным образом, но закономерно изменяется другая статистическая характеристика (показатели вариации, асимметрии, эксцесса и т.п.), то связь является не корреляционной, хотя и статистической. [c.228]
В-пятых, распределение признаков, включаемых в модель, должно быть близким к нормальному. Существуют различные статистические методы проверки нормальности распределения (самый простой — через показатели асимметрии и эксцесса). Выполнение этого требования в экономических исследованиях нередко сопряжено с существенными трудностями и не всегда возможно. [c.83]
Основной особенностью корреляционного анализа следует признать то, что он устанавливает лишь факт степени тесноты связи, не вскрывая ее причин. Кроме того, не существует общеупотребительного критерия проверки нормальности совместного распределения анализируемых переменных, поэтому обычно ограничиваются проверкой нормальности частных одномерных распределений. В условиях малых выборок подобная проверка может быть осуществлена с помощью показателей асимметрии и эксцесса, рассчитываемых через показатели центральных моментов третьего и четвертого порядков и среднее квадратическое отклонение. [c.119]
Описательная статистика вычисляет статистические показатели среднее, медиана, стандартное отклонение, эксцесс, интервал, максимум, счет, k-й наименьший, k-й наибольший, стандартная ошибка, мода, дисперсия, асимметричность, минимум, сумма, доверительный интервал для заданного уровня надежности. Результаты описательной статистики выводятся в указанное место (текущий лист, другой лист, новая книга). [c.462]
Показатель Среднее СКО Вариация Асимметрия Эксцесс [c.103]
Показатели формы распределения - эксцесс. [c.23]
Чрезвычайно важным показателем формы распределения является безразмерный показатель, называемый эксцессом. Эксцесс обозначается как или Ех. Эксцесс характеризует [c.23]
Эксцесс распределения однозначно определяется показателем степени а = Г(1/а)Г(5/а)/[Г(3/а)]2. [c.42]
Соответственно, из вычисленного по выборке случайных величин значения оценки эксцесса, можно определить оценку показателя а. [c.42]
Показатель степени был найден из значения оценки эксцесса распределения, так как для обобщенного экспоненциального распределения показатель степени и эксцесс имеют взаимно однозначное соответствие [c.89]
Показатель в знаменателе влияет на эксцесс. До настоящего момента эксцесс был равен 2, но мы можем изменить его, изменив значение показателя. Теперь формулу нашей характеристической функции можно записать следующим образом [c.122]
В нормальном распределении показатель эксцесса Е = 0. Если Е > О, то данные густо сгруппированы около средней, образуя островершинность. Если Е < 0, то кривая распределения будет плосковершинной. Однако, когда отношения А/та и Е/те меньше 3, то асимметрия и эксцесс [c.143]
Идентификация случайных параметров модели осуществляется с использованием стандартных программ, входящих в состав математического обеспечения современных универсальных ЭВМ. Так, например, в математическом обеспечении ЕС ЭВМ имеется программа, осуществляющая расчет эмпирического распределения, ее сравнение с множеством теоретических законов распределения (нормальное, равномерное, Вейбулла, гамма, экспоненциальное и т. п.), проверку гипотезы о соответствии выбранного закона распределения эмпирическим данным. Проверка гипотезы осуществляется по критериям Пирсона, Романовского, Колмогорова—Смирнова. Программа обеспечивает расчет основных параметров выбранного закона распределения — математического ожидания, дисперсии, среднеквадратического отклонения, показателей эксцесса и асимметрии и коэффициента вариации. [c.96]
Математическое ожидание Дисперсия Среднее квадрати-ческое отклонение 0,89069 -01 0,3SOf>OE-03 0.19509Я-01 Показатель асимметрии Показатель эксцесса Коэффициент вариации 0,22514 -0,82376 21,903 [c.221]
Статистики определяют средние значения как показатели центра распределения. Статистические показатели, которые описывают или измеряют, как данные распределены вокруг среднего значения, известны как показатели вариации. Величины, определяющие симметричность данных, называются показателя ми асимметрии или мерами скошенности, а выражающие пико-вость данных — показателями эксцесса. [c.67]
Средние величины позволяют сделать вывод о центральном или наиболее общем значении, найденном для совокупности данных, меры рассеяния (вариации) показывают, как данные распределены вокруг средней. Показатели скошенности (асимметрии) иллюстрируют степень левосторонней асимметрии, т.е. отрицательной, или правосторонней, т.е. положительной, в распределении частот. Показатели эксцесса определяют уровень островершинности или шюсковершинности распределения частот. [c.77]
В нормальном распределении показатель эксцесса Е=0. Если >0, то данные густо сгруппированы около средней, образуя островершинность. Если <0, то кривая распределения будет плосковершинной. Однако когда отношения A/ma и Е/те меньше 3, то асимметрия и эксцесс не имеют существенного значения, и исследуемая информация соответствует закону нормального распределения. Следовательно, ее можно использовать для корреляционного анализа. [c.41]
Г4 = — — показатель эксцесса (куртозиса), если Г4 J, то распределение [c.2]
Гистограмма имеет ярко выраженный пик и достаточно пологие спады. Островершинность подтверждается еще и значением эксцесса, существенно превышающим эксцесс нормального распределения. Как нам уже известно, распределения с подобными характеристиками могут быть описаны обобщенным экспоненциальным распределением с показателем степени меньше двух. [c.89]
