Вычислите наблюдаемое значение критерия Пирсона по формуле [c.64]
Определите среднее время и интенсивность ц обслуживания покупателей и, используя критерий Пирсона с уровнем значимости а = 0,05, обоснуйте предположение, что время обслуживания распределено по показательному закону. [c.65]
Значение х2-критерия Пирсона при уровне значимости 0,10, 0,05, 0,01 [c.472]
Гипотеза о нормальном законе распределения проверялась по критерию Пирсона, подтвердившему ее. [c.233]
Значения XQ- критерия Пирсона [c.294]
Для того чтобы определить, соответствует ли в нашем примере эмпирическое распределение теоретическому, воспользуемся критерием Пирсона, основанным на определении величины %2, которая вычисляется как сумма квадратов разности эмпирических и теоретических частот, отнесенных к теоретическим частотам [c.109]
В данном анализе при оценке степени согласованности эмпирического и теоретического распределения использовался основанный на критерии Пирсона критерий согласия В. И. Романовского [c.190]
После построения гистограммы распределения можно выдвинуть гипотезу о том, что данная гистограмма может быть аппроксимирована одним из изученных ранее законов распределения. При этом степень близости гистограммы и принятой аналитической модели может быть проверена с использованием критериев согласия. Здесь будет рассмотрен один из этих критериев - критерий Пирсона. [c.87]
Исследуемое эмпирическое распределение имеет 27 столбцов. Аналитическая модель имеет 3 параметра. Следовательно, число степеней свободы для критерия Пирсона равно [c.89]
| Таблица 5. Значение %2 критерия Пирсона при уровне значимости | 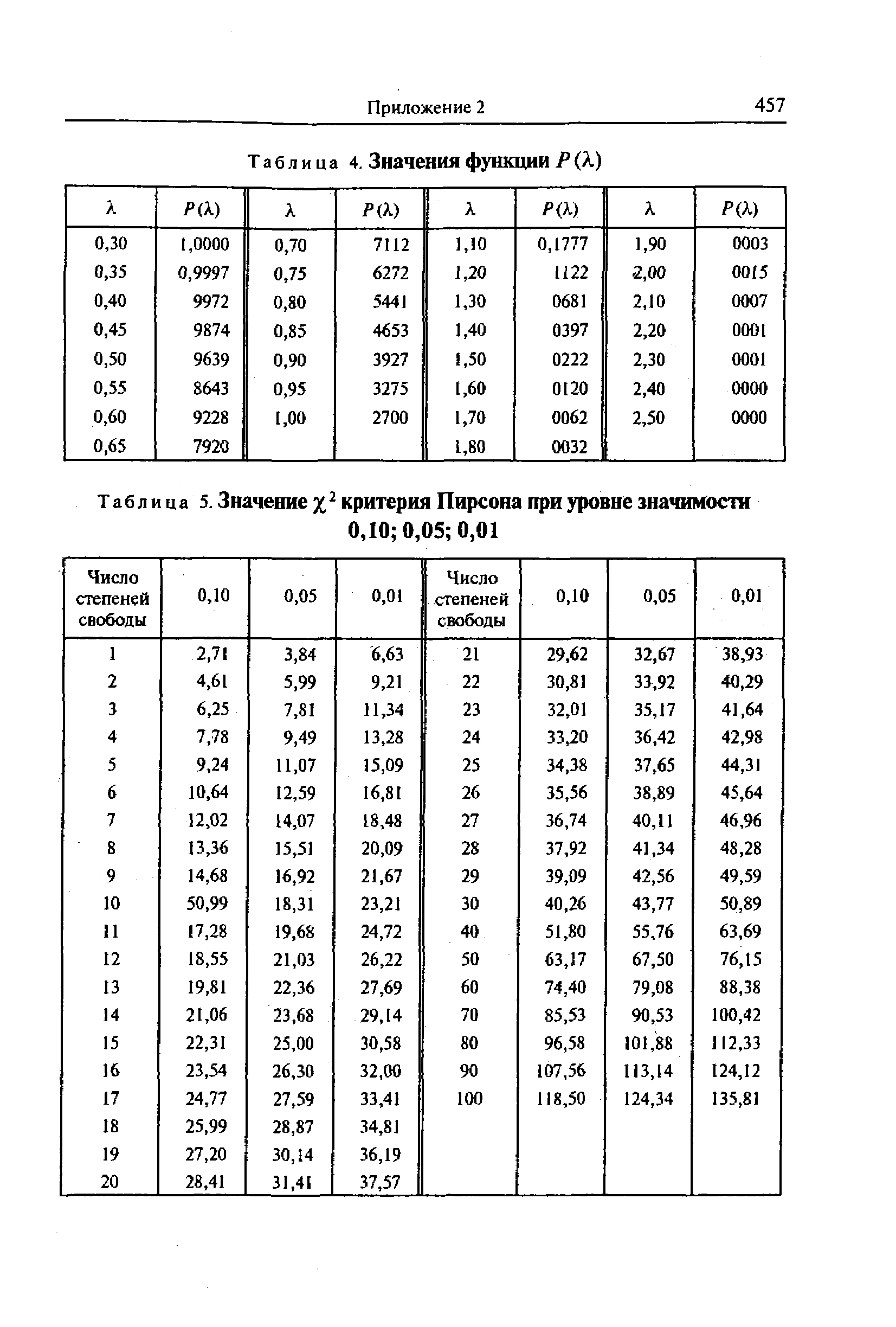 |
При проверке гипотез о виде распределения с помощью критерия Пирсона следует учитывать некоторые условия и допущения, влияющие на полученный результат. [c.73]
Пример. Используя критерий Пирсона при уровне значимости a = 0,05 проверить, согласуется ли гипотеза Н0 о нормальном распределении генеральной совокупности х с эмпирическим распределением выборки объема п = 200 (табл. 2.10). [c.73]
Значение критических точек критерия Пирсона % 2 (хи-квадрат) при разных уровнях значимости [c.259]
Значение хи-квадрат (критерий Пирсона) определяется по формуле [c.125]
Для С.п.г. используются разные критерии. В частности, когда проверяется согласие между выборочным и гипотетическим распределениями, используется критерий согласия, напр., т.н. критерий Пирсона "хи-квадрат". См. также Ошибка. [c.344]
Используемый критерий Пирсона — х2 Колмогорова — Смирнова [c.22]
Критерий Пирсона выражается следующей формулой [c.33]
Из табл. 2.4 видно, что мощность информационного критерия такая же, как у критерия Пирсона, в то время как вероятность отвергнуть верную гипотезу несколько ниже. [c.35]
ИСПЫТАНИЕ СОГЛАСИЯ С ПОМОЩЬЮ КРИТЕРИЯ ХИ-КВАДРАТ (КРИТЕРИЯ ПИРСОНА). УДОВЛЕТВОРИТЕЛЬНОСТЬ СОГЛАСИЯ [c.178]
Существует метод определения разницы между фактическими и теоретическими значениями и сопоставления результатов с таблицами, который известен под названием испытания согласия с помощью критерия хи-квадрат (критерия Пирсона), где хи есть греческая буква %. Этот метод особенно хорошо пригоден для типа задач, рассмотренных в разделе 11.2. Он позволяет проверить, значимо ли отличаются наблюденные частоты распределения от теоретически ожидаемых. Хи-квадрат задается формулой [c.178]
Применение критерия Пирсона к заводскому эксперименту. Предположим, что завод является пред- [c.179]
Для того чтобы ответить на этот вопрос, нужно вычислить распределение дефектов, предположив, что распределение Пуассона, соответствующее старому методу, не отличается от такового для нового метода, и определить значимость по критерию Пирсона. [c.180]
Мы вкратце коснулись проблемы нулевой гипотезы и критерия Пирсона, но читателю следует иметь в виду, что существует много других критериев [c.181]
Рассчитанную величину коэффициента конкордации следует взвешивать по критерию Пирсона (X2) с определенным уровнем значимости (В), т.е. с максимальной вероятностью неправильного результата работы экспертов. Обычно задавать значимость достаточно в пределах 0,005 — 0,05. [c.161]
Табличные величины критерия Пирсона Х [c.161]
В случае определения несогласованности мнений экспертов по коэффициентам конкордации и соответствующей проверке его величины по критерию Пирсона экспертные опросы следует повторить. Если при использовании экспертного метода ранги объектов экспертизы не определяются, то для расчета коэффициента конкордации следует в них перевести, приписывая самому большему количеству предпочтений ранг 1, следующему по важности — 2 и т.д. В противном случае согласованность мнений экспертов следует оценить по критерию согласия Д. [c.162]
Оценка неслучайности согласия мнений экспертов производится с помощью критерия Пирсона по величине %2 = V5 при числе [c.201]
Совместные распределения количественных признаков. Условные распределения. Независимость признаков. Критерий Пирсона. Таблица сопряженности. Регрессионный и корреляционный анализ. Метод наименьших квадратов. Коэффициент корреляции. Дисперсионный анализ однофакторный, многофакторный без повторений. Анализ временных рядов. Тренд, сглаживание, сезонность, циклы. Стационарные ряды. Динамические регрессии. Ложная регрессия. Коинтеграция. [c.49]
Критерий х или критерий Пирсона. [c.229]
Операторы 27—29. Вычисление критерия согласия Пирсона — х2. [c.77]
В главе 5 отмечалось, что близость средней арифметической величины, медианы и моды указывает на вероятное соответствие изучаемого распределения нормальному закону. Но более полная и точная проверка соответствия распределения гипотезе о нормальном законе производится с использованием специальных критериев, из которых рассмотрим наиболее употребимый критерий %2 (хи-квадрат) К. Пирсона. [c.198]
Другими словами, критическая область должна быть такой, чтобы при заданном уровне значимости мощность критерия 1 — р была максимальной. Задача построения такой критической области (или, как говорят, построения наиболее мощного критерия) для простых гипотез решается,с помощью теоремы Неймана—Пирсона, излагаемой в более полных курсах математической статистики. [c.47]
Затем найдем по распределению Пирсона вероятности достижения х2 данного значения Р (я2), т. е. определим вероятность Р (х2) для полученного нами критерия %2, при этом воспользуемся данными, приведенными в специальной таблице . В нашем [c.109]
Т а б л и ц а 3 Таблица вероятностей Р для критерия х2 К. Пирсона [c.130]
Идентификация случайных параметров модели осуществляется с использованием стандартных программ, входящих в состав математического обеспечения современных универсальных ЭВМ. Так, например, в математическом обеспечении ЕС ЭВМ имеется программа, осуществляющая расчет эмпирического распределения, ее сравнение с множеством теоретических законов распределения (нормальное, равномерное, Вейбулла, гамма, экспоненциальное и т. п.), проверку гипотезы о соответствии выбранного закона распределения эмпирическим данным. Проверка гипотезы осуществляется по критериям Пирсона, Романовского, Колмогорова—Смирнова. Программа обеспечивает расчет основных параметров выбранного закона распределения — математического ожидания, дисперсии, среднеквадратического отклонения, показателей эксцесса и асимметрии и коэффициента вариации. [c.96]
Пирсон (Pearson) Эгон Шарп (1895—1980), английский математик, специалист полга-тематической статистике. Окончил Кембриджский университет в 1933— 1960 гг. — профессор Лондонского университета. Один из авторов (совместно с Ю. Нейманом) общей теории проверки статистических гипотез одно из важнейших понятий ее — т.н. критерий Пирсона. [c.447]
