Вероятность (1 — Р) не допустить ошибку 2-го рода, т. е. отвергнуть гипотезу HQ, когда она неверна, называется мощностью (или функцией мощности) критерия. [c.47]
Другими словами, критическая область должна быть такой, чтобы при заданном уровне значимости мощность критерия 1 — р была максимальной. Задача построения такой критической области (или, как говорят, построения наиболее мощного критерия) для простых гипотез решается,с помощью теоремы Неймана—Пирсона, излагаемой в более полных курсах математической статистики. [c.47]
Мощность критерия 47 Мультиколлинеарность 21, 108—111 [c.302]
Критерий прямое или косвенное отнесение затрат на носители и места возникновения затрат Критерий поведение видов затрат по отношению к уровню загрузки производственных мощностей Критерий прямое отнесение затрат на носители и места возникновения затрат [c.184]
Вероятность ошибки второго рода обозначают р. Вероятность дополнительного события, т.е. правильного отклонения гипотезы Я0 называется мощностью критерия. Следовательно, мощность крите- [c.59]
Вид сделки Загрузка мощностей Критерий принятия решений Модель принятия решений [c.250]
Сравнение мощности критериев осуществлялось в несколько этапов. [c.33]
Сравнительный анализ мощности критериев х2 и У, [c.35]
Мощностью критерия называется вероятность того, что нулевая гипотеза будет отвергнута, если верна альтернативная гипотеза. Вероятность отвергнуть нулевую гипотезу определяется следующим выражением [c.60]
Табл. 3.3 и рис. 3.6 отражают результаты сравнения функции мощности критерия и экспериментальной кривой, полученной методом имитационного моделирования. В каждом эксперименте генерировались выборки объемом п = 10, 15, 20 и 50 из нормальной генеральной совокупности с постоянной дисперсией OQ = 1 и переменным средним значением х . В выборках подсчитывалось количество случайных величин, вышедших за границы контроля, и проверялось условие (3.21). [c.61]
Эксперименты для каждого значения xl (или q) повторялись 1000 раз. Относительное число отвергнутых гипотез и является значением экспериментальной функции мощности критерия значимости. [c.61]
| Рис. 3.5. Кривые мощности критерия. Границы контроля 1 — 0,431 2 — 1,000 3 — 2,000 4 — 3,000. X — функция мощности среднего арифметического | 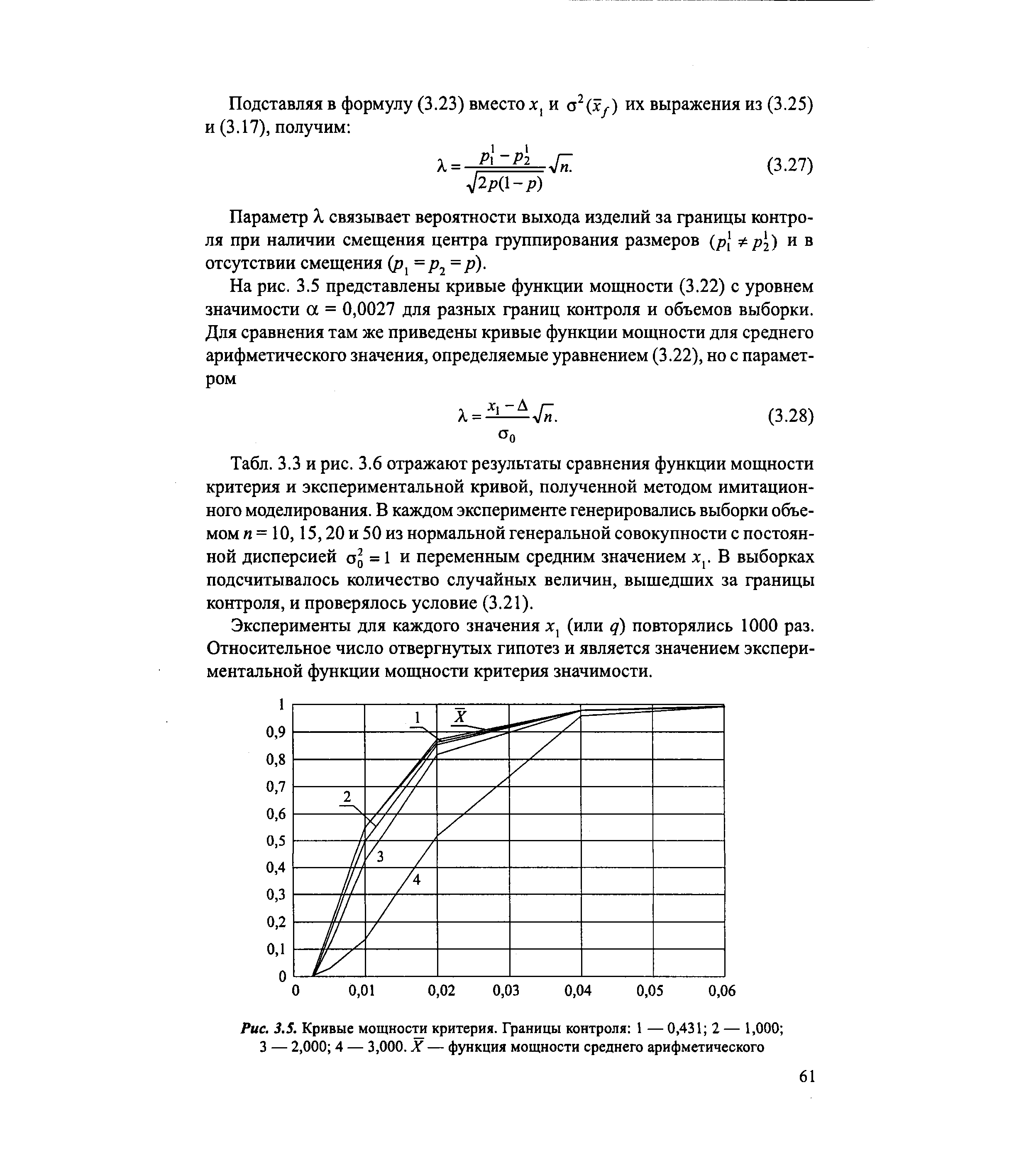 |
Анализ устойчивости критерия (3.21) показал, что с ростом степени "засорения" мощность критерия по обеим оценкам снижается, поскольку увеличивается вероятность отвергнуть нулевую гипотезу, когда она верна. Однако критерий значимости изменения состояния ТП для альтернативного среднего устойчивее, чем для среднего арифметического значения, что в принципе вполне логично и объясняется следующим. Для альтернативного среднего выход резко выделяющегося значения случайной величины за [c.63]
Информационный метод анализа точности и стабильности ТП повышает информативность контроля по альтернативному признаку. В основе метода лежит предложенная оценка смещения центра рассеивания размеров — альтернативное среднее, рассчитываемое по результатам альтернативного контроля, т. е. без измерений. Показано, что распределение альтернативного среднего имеет условия сходимости к нормальному распределению. Свойство нормальности распределения альтернативного среднего позволило предложить критерий значимости смещения центра рассеивания размеров относительно середины поля допуска. Это дает возможность оценить текущее состояние ТП более оперативно по сравнению с традиционными методами анализа точности и стабильности, поскольку в качестве исходных данных используются результаты, полученные с помощью предельных калибров, а не результаты измерения каждой детали. Предлагаемый критерий значимости изменения состояния ТП устойчивее к "засорениям", чем критерий, определяемый с помощью среднего арифметического значения. Влияние погрешностей измерения на мощность критерия для альтернативного среднего также меньше, чем на мощность критерия для среднего арифметического. [c.67]
Статистическая обработка результатов наблюдений. Правила оценки средних значений и дисперсий Статистическая обработка результатов наблюдений. Мощность критериев оценки средних значений и дисперсий. Проект [c.31]
Мы строили критическую область исходя из требования, чтобы вероятность попадания в нее критерия К была равна а, при условии, что нулевая гипотеза справедлива. Не менее важно знать также вероятность попадания критерия К в критическую область при условии, что нулевая гипотеза неверна и, следовательно, справедлива конкурирующая. Эта вероятность определяет мощность критерия. [c.27]
Наивыгоднейшим является такое распределение нагрузки между электростанциями, при котором обеспечиваются минимальные затраты в энергосистеме на получение данного количества электроэнергии. Так как речь идет о наилучшем использовании имеющихся мощностей, критерием (принципом) выбора наивыгоднейшего варианта распределения заданного графика нагрузки может служить минимум себестоимости продукции при неизменных капитальных затратах (см. гл. 7). Вместе с тем для энергосистем распределение нагрузки на минимум себестоимости электроэнергии практически равнозначно распределению на минимум затрат на топливо, так как все остальные эксплуатационные расходы (на заработную плату, амортизационные отчисления и пр.) очень в малой степени зависят от распределения нагрузки. [c.195]
Вероятность совершить ошибку первого рода принято обозначать буквой а, и ее называют уровнем значимости. Вероятность совершить ошибку второго рода обозначают / . Тогда вероятность несовершения ошибки второго рода (1 - р) называется мощностью критерия. [c.72]
Что определяет мощность критерия [c.86]
Можно фиксировать а в уравнении (34). Тогда определение в альтернативной гипотезе HI i = дает конкретное р. Считая р функцией pix в уравнении (35), мы получим оперативные характеристики критерия. Дополнение р, т. е. (1 — Р), называется мощностью критерия (ср. уравнения (88) — (91) далее в этом параграфе). [c.133]
Для малых п мощность критериев мала. Это менее важно, если мы хотим применить один из ММС, и только в случае сильного нарушения нормальности и наличия гетероскедастичности отклоняем нуль-гипотезу. [c.212]
Протяженность ряда и мощность критерия [c.3]
Этот пример иллюстрирует то обстоятельство, что при добавлении в статистическую модель излишних объясняющих переменных (в т.ч. и константы) мощность критерия снижается, и отвергнуть гипотезу единичного корня становится трудно, даже если она не верна. Поэтому важно выбирать статистическую модель "без излишеств", включая в нее только такие составляющие, которые соответствуют поведению наблюдаемого временного ряда. [c.126]
Последняя серия результатов показывает, что при увеличении количества наблюдений мощность критериев Дики - Фуллера возрастает. [c.131]
В связи с последним примером, следует особо отметить, что использование расширенной модели предполагает, что количество запаздывающих разностей, включенных в правую часть, исчерпывает временную зависимость, так что et -независимые случайные величины. В то же время, не следует включать в правую часть излишних запаздывающих разностей, т.к. это снижает мощность критериев как по причине оценивания дополнительных параметров, так и по причине уменьшения используемого количества наблюдений. [c.133]
Неправильный выбор оцениваемой статистической модели может существенно отразиться на мощности критерия Дики - Фуллера. Например, если наблюдаемый ряд порождается моделью случайного блуждания со сносом, а статистические выводы производятся на основании результатов оценивания статистической модели без включения в ее правую часть трендовой составляющей, то тогда мощность критерия, основанная на статистике tp, стремится к нулю с возрастанием количества наблюдений [c.135]
Такой неожиданный результат объясняется тем, что пополнение статистической модели (SM) дополнительными регрессорами требует их оценивания, что снижает, в конечном счете, мощность критерия. Поэтому желательно при проверке гипотезы единичного корня оценивать SM, выбираемую "без запаса". Однако при отсутствии информации о том, равен нулю снос в DGP или нет, при отклонении гипотезы единичного корня следует опираться на консервативное значение, даваемое таблицами Фуллера. Иначе мы можем ошибочно отвергать эту гипотезу более, чем в 5% случаев, если в действительности снос в DGP отсутствует. [c.138]
Возможно, что это связано с пониженной мощностью критериев из-за включения в модель лишней объясняющей переменной t. [c.141]
Статистические выводы, полученные с применением статистик DF и РР, здесь совпадают и указывают на возрастание мощности критериев при увеличении количества наблюдений. [c.148]
А. Хальд [30] предложил оценивать чувствительность контрольных карт к изменению параметра процесса при помощи функции мощности критерия. Это предложение непосредственно вытекает из теории проверки статистических гипотез Неймана и Пирсона, согласно которой предпочитается один критерий другому, если первый критерий при всех возможных альтернативных значениях неизвестного параметра распределения дает большую вероятность обнаружения ложности проверяемой гипотезы, чем второй. Идея приложения теории проверки статистических гипотез к задачам обнаружения разладки технологических процессов оказалась весьма продуктивной и нашла широкое применение в теории всех видов контрольных карт. [c.118]
Гипотезы и критерии. Постановка задачи о проверке гипотез. Основные виды гипотез. Вероятности ошибок. Мощность критерия. Проверка двух простых гипотез. Способы сравнения критериев. Понятие НМК. Лемма Нейман-Пирсона. Простая гипотеза и сложная альтернатива. Понятие РНМК. [c.31]
Но существует плата за пользование уровнем ошибки, устанавливаемой в эксперименте. Если мы хотим, чтобы все т суждений в эксперименте были правильными, то длины индивидуальных доверительных интервалов должны возрасти. Например, в одном из методов оцениваемое стандартное "отклонение умножается не на t%f2> а на (юльшую величину /(2" )- В терминах проверки гипотез из ММС нмтекает, что такой критерий менее чувствителен к отклонениям от //о == (j,2 =. ..== (г/( и метод становится менее мощным по сравнению с несовместным методом. В [Miller, 1966, р. 32—33] упомянуты фи возможности для уменьшения длины интервала и увеличения мощности критерия. [c.173]
Уменьшение числа утверждений т. Число т зависит от числа факторов и числа их уровней. Если мы имеем один фактор с k уровнями, то хотелось бы реализовать для всех т утверждений относи-юльно k средних. Если, однако, существует много утверждений из-за гого, что много факторов, то мы можем определить мощность критерия, выбирая аЕ для всех суждений только относительно основных >ффектов или всех суждений относительно одного определенного фактора. В таком случае формируются семейства близких суждений in общего множества т суждений, и внутри каждого семейства определяется уровень ошибок. Этот уровень называется уровнем ошибки для семейства и используется вместо уровня для всего эксперимен-ш. В V.B.3 мы вернемся к образованию семейств. Мы согласны с (Miller, 1966, р. 34—35], что выбор семейств производится из субъек-швных соображений. (В любом случае экспериментатор должен иметь II виду различные уровни.) [c.173]
Как мы отмечали в V.B.2, выбор типа уровня ошибки, который стоит задавать в эксперименте,—это довольно спорный вопрос. Поскольку выбор уровня ошибки на сравнение приводит во многих случаях к ложным результатам, мы ее отвергли. Выбор между уровнями ошибки в эксперименте или на семейство более труден. Чтобы не ухудшить мощность критериев, мы рекомендовали подход с заданием уровня ошибки на семейство гипотез, где под семейством здесь понимаются все утверждения, относящиеся к одной определенной комбинации факторов плана 2 у3 Кроме типа уровня ошибки, мы должны задать еще и ее значение. Определение таких значений весьма произвольно. (Подход теории статистических решений, основанный на функциях потерь, также произволен, поскольку трудно определить потери в нашем эксперименте.) Обычно в статистике ис пользуют значение ошибки, равное 5%, хотя берут также и значения 1 0 и 1 %. В случае одновременных выводов можно следовать, например, [Dunn, 1964, р. 248] и использовать большие значения ошибки, скажем 20%. Чтобы дать возможность читателю выбрать значения для а или aF, мы приводим результаты для различных значений а и aF. Мы сами предпочли а = = 0,20 для того, чтобы не ухудшать мощностей частных критериев. [c.294]
Пусть вероятность ошибки второго рода раина Р, тогда чисто 1 р на-.jtbiuaioT мощностью критерия. Чем больше мощность критерия, шм меньше вероятность ошибки второго poia. При выбранном уровне начнмогти критическую область следует строить так, чтобы мощность критерия была максимальной. [c.228]
Смотреть страницы где упоминается термин Мощность критерия
: [c.306] [c.60] [c.19] [c.76] [c.173] [c.309] [c.131] [c.136] [c.146] [c.147]Смотреть главы в:
Информационные методы в управлении качеством -> Мощность критерия
Маркетинговые исследования Издание 3 (2002) -- [ c.366 ]
