Табл. 3.3 и рис. 3.6 отражают результаты сравнения функции мощности критерия и экспериментальной кривой, полученной методом имитационного моделирования. В каждом эксперименте генерировались выборки объемом п = 10, 15, 20 и 50 из нормальной генеральной совокупности с постоянной дисперсией OQ = 1 и переменным средним значением х . В выборках подсчитывалось количество случайных величин, вышедших за границы контроля, и проверялось условие (3.21). [c.61]
Эксперименты для каждого значения xl (или q) повторялись 1000 раз. Относительное число отвергнутых гипотез и является значением экспериментальной функции мощности критерия значимости. [c.61]
| Рис. 3.5. Кривые мощности критерия. Границы контроля 1 — 0,431 2 — 1,000 3 — 2,000 4 — 3,000. X — функция мощности среднего арифметического | 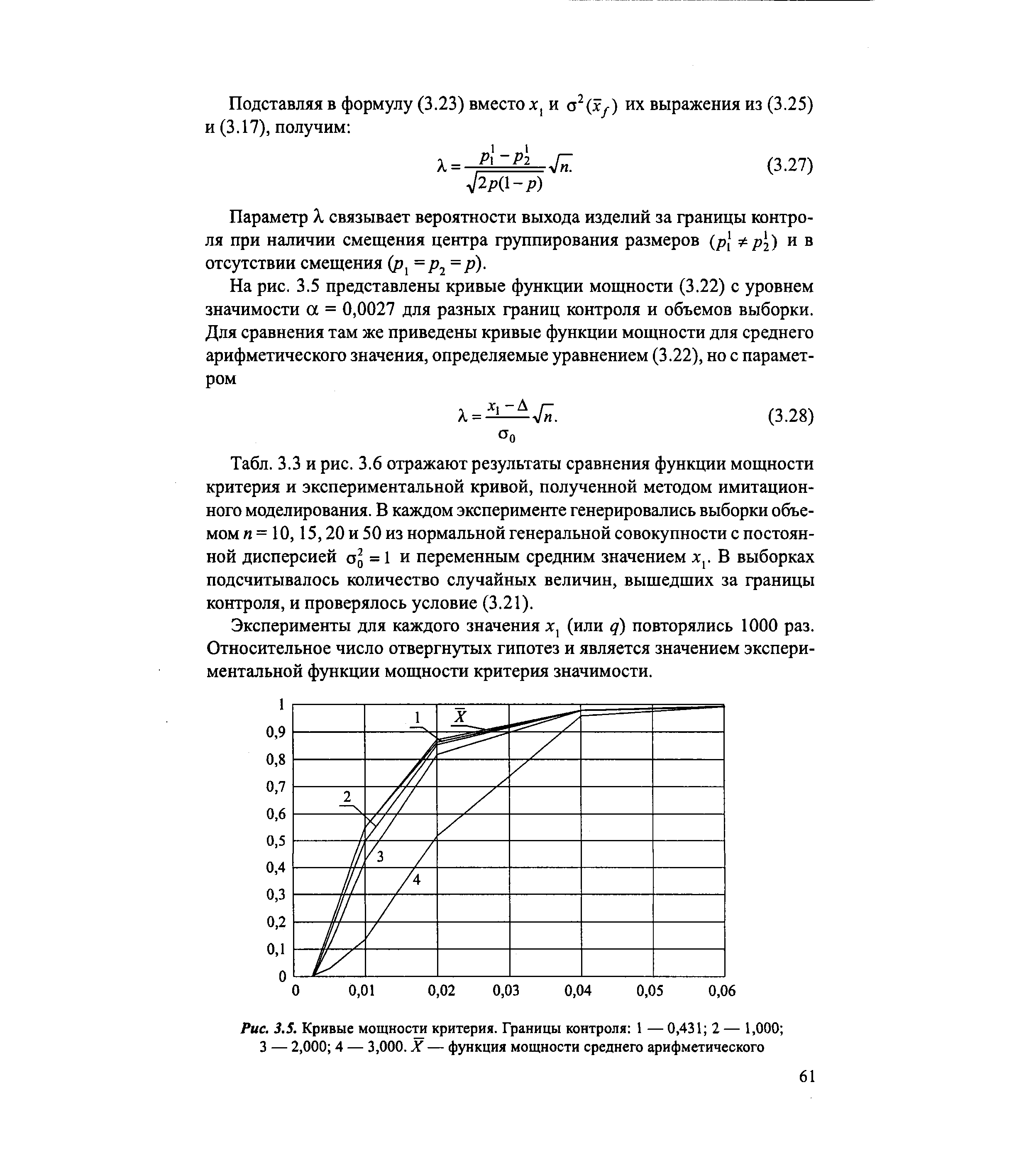 |
Целый ряд задач, связанных с размещением производственных мощностей для нефтегазодобывающих предприятий, предприятий РАО ЕЭС , металлургических комплексов, транспортных узлов, с выбором типоразмеров транспортных средств, в частности, самолетов, тяжелых грузовиков и тому подобного, требуют решения задач размещения с похожими целевыми функциями и критериями их оценки. Большинство перечисленных задач предполагают наличие группы взаимосвязанных целевых функций, сочетающих одновременно решение транспортной задачи по минимизации транспортной работы, связанной с сообщением между размещенными объектами, с максимальной доступностью размещенных объектов до центров тяготения населения, баз снабжения или ремонта, хранилищ нефти, газа, ископаемых ресурсов, массовых посевов сельскохозяйственных культур и т.п. Таким образом, с одной стороны, стоит задача максимально централизовать или собрать все объекты воедино для лучшей управляемости, снижения транспортных затрат и, следовательно, себестоимости, а с другой стороны, требуется решить прямо противоположную задачу — максимизировать доступность до рынков сбыта или потребления. [c.134]
Можно фиксировать а в уравнении (34). Тогда определение в альтернативной гипотезе HI i = дает конкретное р. Считая р функцией pix в уравнении (35), мы получим оперативные характеристики критерия. Дополнение р, т. е. (1 — Р), называется мощностью критерия (ср. уравнения (88) — (91) далее в этом параграфе). [c.133]
Влияние ввода ограничений на величину оптимизируемого критерия лучше всего рассмотреть графически. Пусть известна зависимость принятого критерия у (скажем, прибыли) от фактора х (например, мощности предприятия), изображенная на рис. 2.3 функцией у = f(x). Максимальное значение критерия г/, достигается в точке / при значении фактора , . Однако ввод ограничений [c.31]
Модель оптимальной технологической схемы, проектируемого (реконструируемого) нефтеперерабатывающего предприятия позволяет определить набор и потребную мощность технологических процессов и установок, рассчитать материальные балансы, определить рациональные рецепты смешения товарной продукции. Так как строительство (реконструкция) предприятия связано с дополнительными капитальными и эксплуатационными затратами, то в качестве целевой функции (критерия оптимальности) используется показатель минимума приведенных затрат. [c.157]
Постановки задач планирования экономики рассмотренного здесь типа получили широкое распространение в шестидесятых годах (конечно, модели, предназначенные для планирования народного хозяйства, были значительно более сложными", чем модель (2.15)). Однако попытки практического внедрения моделей такого типа показали, что построить единственный критерий удовлетворительным образом не удается, т. е. не удается подобрать вектор с так, чтобы его составляющие действительно отражали роль различных компонент конечного продукта в развитии страны. Эти трудности связаны не только с принципиальными проблемами формулировки целевой функции потребления (ЦФП), о которых уже говорилось в гл. 2, но п с недостатками статических моделей. В самом деле, в конечный продукт народного хозяйства у входят капиталовложения в новые производственные фонды, личное потребление населения, расходы на содержание государственного аппарата ц обороту, сальдо экспорта и импорта и т. д. Если даже пренебречь влиянием внешней торговли, считать расходы па оборону и управление фиксированными, то все равно останутся капиталовложения, которые в рассмотренной нами модели, вообще говоря, являются бессмысленными, поскольку никак не отражаются па мощностях отраслей. Поэтому вводить оценку капитальных вложений приходится волевым , экспертным образом. Хотелось бы оценить роль вложений в основные фонды внутри самой модели. Для этого модель должна быть построена так, чтобы в ней учитывалось влияние капиталовложений на возможности производства. Такими моделями являются динамические многоотраслевые модели. [c.269]
Укрупненная оценка качества исполнения функций по вариантам (блок 14) выполнялась экспертным путем с учетом следующих критериев объема аппаратуры, потребляемой мощности, надежности, удобства пользования и т. д. [c.84]
Категория полного хозяйственного расчета значительно шире самофинансирования. Полный хозрасчет невозможен без внедрения ряда других методов хозяйствования, к примеру методов экономического стимулирования и правового обеспечения. Организация полного хозрасчета на предприятиях базируется на совокупности не только всех экономических форм и методов управления производством, но и на более полном их использовании. Так, с позиции самофинансирования оценка результатов деятельности осуществляется по показателю прибыли, а в условиях полного хозрасчета главнейшим критерием оценки деятельности предприятий и материального поощрения трудовых коллективов, в первую очередь, является выполнение договорных обязательств по поставкам продукции. Аналогичная ситуация имеет место, допустим, в ценообразовании, когда при самофинансировании важен уровень оптовых цен, обеспечивающий рентабельность, необходимую для расширенного воспроизводства, а для организаций, работающих в условиях полного хозрасчета, большое значение имеет и стимулирующая функция оптовых цен. Например, уровень и структура тарифов на электроэнергию должны не только соответствовать требованию самофинансирования, но и способствовать снижению заявляемого максимума потребляемой мощности, выравниванию суточного и сезонного графиков нагрузки, энергосбережению и т.п. [c.70]
Число ограничений может быть дополнено и условиями мобильности производственных мощностей, т. с. возможностью переброски мощностей для производства разных изделий, спросом, производственными связями и требованиями выполнения важнейшей номенклатуры, НЧП, прибыли и т. д. Исходя из условий задачи оптимизация производственного плана состоит в максимизации целевой функции (критерия оптимальности) на основе оценки эффективности каждого вида продукции (кэ-) и увеличения его выпуска (AXj) [c.265]
Конкуренция производителей (теплоисточников). Реализация этой формы прямой конкуренции потребует решения технических, организационных и правовых вопросов. Так, конкуренция теплоисточников принципиально возможна только в крупных закольцованных перемычках и системах централизованного теплоснабжения. Необходимо разделение функций производства и передачи теплоэнергии, т.е. создание независимой регулируемой теплосетевой организации, не имеющей собственных, по крайней мере крупных, теплоисточников. Должен быть законодательно обеспечен свободный доступ производителей к единой теплосети системы. Тогда при наличии избыточных теплогенерирующих мощностей оператор рынка (теплосетевая компания) может осуществлять экономически целесообразные переключения нагрузок, например, по критерию минимума стоимости генерирования (отпускной цены) в данный период, конечно, с учетом инерционности теплового потока. Ограничением для применения данной модели может стать сложившаяся конфигурация тепловой сети, препятствующая подключению новых теплоисточников без нарушения гидравлического режима. [c.165]
Отношения (2.8) и (2.9) не являются связными, так как для произвольных векторных оценок w(a), w(b) часть неравенств (2.8) может выполняться "в одну сторону", (т. е. w.(a) > > w.(b)), а остальные — "в другую сторону" (го.(а) < го.(Ь)). Такие векторные оценки оказываются несравнимыми по Парето и образуют множество недоминируемых оценок, которым соответствует множество недоминируемых (эффективных по Парето) альтернатив. Таким образом, отличительной особенностью недоминируемых или эффективных по Парето альтернатив является то, что ни у одной из них ни по одному из их частных критериев оценка не может быть улучшена без ухудшения оценки какого-то другого (или других) критерия. Следовательно, эффективные альтернативы между собой несравнимы, и на множестве значений векторных оценок можно определить результат применения функции выбора. Этот результат применения функции выбора на множестве значений векторных оценок будем называть ядром отношения по заданной информации о предпочтениях ЛПР и обозначать eff(w,inf). Таким образом, ядро отношения Парето получит обозначение eff(w,iop). Для задач с положительно ориентированными критериями ядро eff(w,iop) отношения Парето расположено в северо-восточном направлении на границе достижимого множества векторных оценок. При этом мощность множества оценок ядра может быть различной в зависимости от конкретных особенностей (в частности, кон- [c.175]
Вторая фаза. Из собранной информации надо выделить действительно относящуюся к делу, проанализировать и оценить ее точность, достоверность и достаточность. В результате аналитической работы должны быть подготовлены альтернативные предложения по решению рассматриваемой проблемы. Из них менеджер, несущий ответственность за результаты принятия решения, выберет наиболее рациональную с точки зрения достижения высоких конечных результатов деятельности, включая удовлетворение потребностей внешней среды и максимально эффективное использование имеющихся возможностей (ресурсов) в соответствии с выбранными критериями оценки. Решение должно быть тесно связано с организационными механизмами оператора, действующей системой мотивации работников и делегирования им полномочий, а также с особенностями технологического процесса по производству услуг или выполняемых функций, обеспечивающими приемлемые конечные результаты деятельности. Конечные результаты деятельности включают показатели, отражающие финансовое состояние организации, экономические результаты, производственные результаты, результаты технического развития (размеры производственных мощностей, уровень технологии, надежность, живучесть), социальные результаты (уровень развития персонала, уровень социальной защищенности и др.). [c.62]
В предлагаемом учебном пособии мы даем краткое введение в современные методы эконометрического анализа статистических данных, представленных в виде временных рядов, которые учитывают возможное наличие у рассматриваемых переменных стохастического тренда. Основные акценты, как и в работе [Носко (2000)], смещены в сторону разъяснения базовых понятий и основных процедур статистического анализа данных с привлечением смоделированных и реальных экономических данных. Вместе с тем, от читателя требуется несколько большая осведомленность в отношении вероятностно-статистических методов исследования. Предполагается, что читатель имеет представление о совместной функции распределения, многомерном нормальном распределении, методе максимального правдоподобия, свойстве состоятельности оценок, характеристиках статистических критериев (ошибки первого и второго рода, мощность), а также владеет методами регрессионного анализа в рамках начального курса эконометрики. Кроме того он должен иметь некоторое представление о комплексных числах и комплексных корнях полиномов. [c.6]
А. Хальд [30] предложил оценивать чувствительность контрольных карт к изменению параметра процесса при помощи функции мощности критерия. Это предложение непосредственно вытекает из теории проверки статистических гипотез Неймана и Пирсона, согласно которой предпочитается один критерий другому, если первый критерий при всех возможных альтернативных значениях неизвестного параметра распределения дает большую вероятность обнаружения ложности проверяемой гипотезы, чем второй. Идея приложения теории проверки статистических гипотез к задачам обнаружения разладки технологических процессов оказалась весьма продуктивной и нашла широкое применение в теории всех видов контрольных карт. [c.118]
Создание АСУ предполагает наличие достаточных вычислительных мощностей для осуществления оптимальных расчетов в необходимые сроки, а также набора экономико-математических моделей оптимизации управленческих задач и решений. Необходимо по каждой конкретной задаче управления четко сформулировать и взаимоувязать целевые функции и критерии оптимальности. Попытки оптимизации отдельно взятых частных функций не могут оказаться успешными, если одновременно не оптимизируются все объективно сопряженные с ними функции. [c.317]
Математич. методы планирования п р о и з-в а. Применение математич. методов существенно повышает точность и качество планирования. При разработке планов произ-ва нек-рые задачи могут быть сформулированы и решены при помощи математич. методов. Среди таких задач важное значение имеет определение т. н. оптимального ассортимента выпуска изделии на предприятиях с многоиоменклатурным произ-вом. Установление оптимального плана имеет важное значение при разработке проекта Т., как отправного материала, представляемого руководящим органам на предварительной стадии составления нар.-хоз. плана. Для установления оптимального плана произ-ва надо руководствоваться определенными экономич. критериями, позволяющими использовать математич. методы, в частности приемы линейного программирования для нахождения оптимального варианта программы выпуска продукции. Среди критериев оптимизации могут быть максимальный объем выпуска товарной продукции, максимальный уровень выработки на 1 работника, максимальный размер накоплений, максимальное использование производств, мощностей, минимальный уровень затрат на произ-во и др. Известно, что методика линейного программирования позволяет определить оптимальный вариант решения поставленной задачи при любом количестве ограничивающих условий, но применительно к одной целевой функции, выражающей критерий оптимальности. При разработке Т. возникает необходимость проанализировать н установить сравнительные достоинства разных вариантов плана произ-ва, составленных применительно к различным критериям оптимизации. Ниже приводится схематич. пример оптимизации программы выпуска 4 изделий (А, Г>, В. Г), исходя из критериев максимального объема товарной продукции, максимальной прибыли и наиболее-полного использования производств, мощности при след, исходных данных (см. табл. 3). [c.194]
Выражение (I) обычно наз. исходной системой уравнений и неравенств, а выражение (II) — функционалом задачи линейного программирования или целевой функцией. Целевая функция является критерием оптимальности. Первая группа неравенств системы (I) позволяет учесть в расчете ограничения в существующих на начало планируемого периода мощностях топливодобывающих предприятий. Вторая группа неравенств учиты- [c.212]
Как мы отмечали в V.B.2, выбор типа уровня ошибки, который стоит задавать в эксперименте,—это довольно спорный вопрос. Поскольку выбор уровня ошибки на сравнение приводит во многих случаях к ложным результатам, мы ее отвергли. Выбор между уровнями ошибки в эксперименте или на семейство более труден. Чтобы не ухудшить мощность критериев, мы рекомендовали подход с заданием уровня ошибки на семейство гипотез, где под семейством здесь понимаются все утверждения, относящиеся к одной определенной комбинации факторов плана 2 у3 Кроме типа уровня ошибки, мы должны задать еще и ее значение. Определение таких значений весьма произвольно. (Подход теории статистических решений, основанный на функциях потерь, также произволен, поскольку трудно определить потери в нашем эксперименте.) Обычно в статистике ис пользуют значение ошибки, равное 5%, хотя берут также и значения 1 0 и 1 %. В случае одновременных выводов можно следовать, например, [Dunn, 1964, р. 248] и использовать большие значения ошибки, скажем 20%. Чтобы дать возможность читателю выбрать значения для а или aF, мы приводим результаты для различных значений а и aF. Мы сами предпочли а = = 0,20 для того, чтобы не ухудшать мощностей частных критериев. [c.294]
Целевая функция и система ограничений могут быть представлены в виде исходной матрицы прямых затрат.. Примерная ее форма показана в табл. 9. Для решения описанной задачи современные ЭВМ имеют стандартные программы. Преимущество такой модели е только в том, что она показывает наиболее рациональную технологическую схему, необходимую производственную мощность каждой из технологических установок, рациональное использование промежуточных продуктов при минимуме приведенных затрат, но и в том, что, пользуясь ею, можно определить, как изменится критерий оптимальности, если один из ограиичен- [c.158]
Вторым обстоятельством, интересующим нас, является смещение самой точки критического соотношения. Если она передвинулась вправо, это значит, что предприятие должно полнее использовать производственную мощность для того, чтобы дело себя оправдало. И наоборот, при меньшем значении точки критического соотношения (перемещение ее влево) это требование не так существенно. Принимая решения, предприятие должно учитывать оба критерия в их взаимной связи. На рис. 29.9 нанесены две линии прибыли, соответствующие двум различным вариантам производства. Вариант А характеризуется более низким положением точки критического соотношения, чем вариант В . Применительно к данному критерию это обстоятельство делает вариант А более желательным, чем вариант В . Однако функция прибыли при варианте В соответствует большей маржинальной прибыли после того, как точка критического соотношения достигнута. Следовательно, этот вариант предпочтительнее с точки зрения другого критерия. Если предприятие имеет возможность работать на уровне, соответствующем точке а на оси абсцисс, оба варианта обеспечи- [c.665]
Целевая функция и система ограничений МОГУТ бьпь представлены и ни.к- исходной матрицы прямых затрат. Примерная ее форма показана в табл. 7. Для решения описанной задачи современные ЭВМ имеют стандартные программы. Преимущество такой модели не только в том, что она показывает наиболее рациональную технологическую схему, необходимую производственную мощность каждой из технологических установок, рациональное использование промежуточных продуктов при минимуме приведенных затрат, но и в том, что на ее основе известно, как изменится критерий оптимальности, если один из ограниченных ресурсов увеличится на единицу, т. е. получается оценка ресурса. Эти оценки получаются в целевой строке симплексной таблицы. ОднакЪ следует учитывать ограниченность этих оценок. Они целиком и полностью зависят от исходных условий, т. е. действуют в определенном пределе. Стандартные программы дают возможность при однократном решении рассчитать устойчивость этих оценок. [c.165]
Как видно из таблицы и рисунков, мощность т-критерия в случае нелинейного тренда вида (1) в основном больше, чем в случае линейного тренда (не говоря уже о квадратичном). Почти на всём своём протяжении функция распределения TNL проходит между функциями для тс и T t- Однако при низких р-значениях, меньших 0.002, TNL < r t. Тем не менее, TNL остаётся большей, чем T tt. Хотя не исключено, что становится меньшей при очень низких р-значениях, меньше 0.00004, но в данной области слиш- [c.58]
