Пример 14.6. Построим линейный тренд процентных ставок по кредитам на основе статистических данных, опубликованных в Бюллетене банковской статистики № 4 (47) за 1997 г. [c.612]
Вторым этапом является поиск значений параметров уравнения. Параметры трендовых моделей определяются с помощью системы нормальных уравнений. В случае применения линейного тренда используют следующую систему уравнений, которую решают способом наименьших квадратов [c.612]
Пример 14.7. Предполагая наличие циклических колебаний, проведем гармонический анализ динамики отклонений от линейного тренда данных о ставках по кредитам (у, — у,). [c.617]
Линейный тренд хорошо отражает тенденцию изменений при действии множества разнообразных факторов, изменяющихся различным образом по разным закономерностям. Равнодействующая этих факторов при взаимопогашении особенностей отдельных фак- [c.322]
При b = 1 имеем линейный тренд, b = 2 - параболический и т.п. Степенная форма - гибкая, пригодная для отображения изменений с разной мерой пропорциональности изменений во времени. Жестким условием является обязательное прохождение через начало координат при t = 0, у = 0. Можно усложнить форму тренда у = а + th или у = а + th, но эти уравнения нельзя логарифмировать, трудно вычислять параметры, и они крайне редко применяются. [c.325]
| Таблица 9.4 Проверка гипотезы о линейном тренде индекса цен (1990 г. = 100%) | 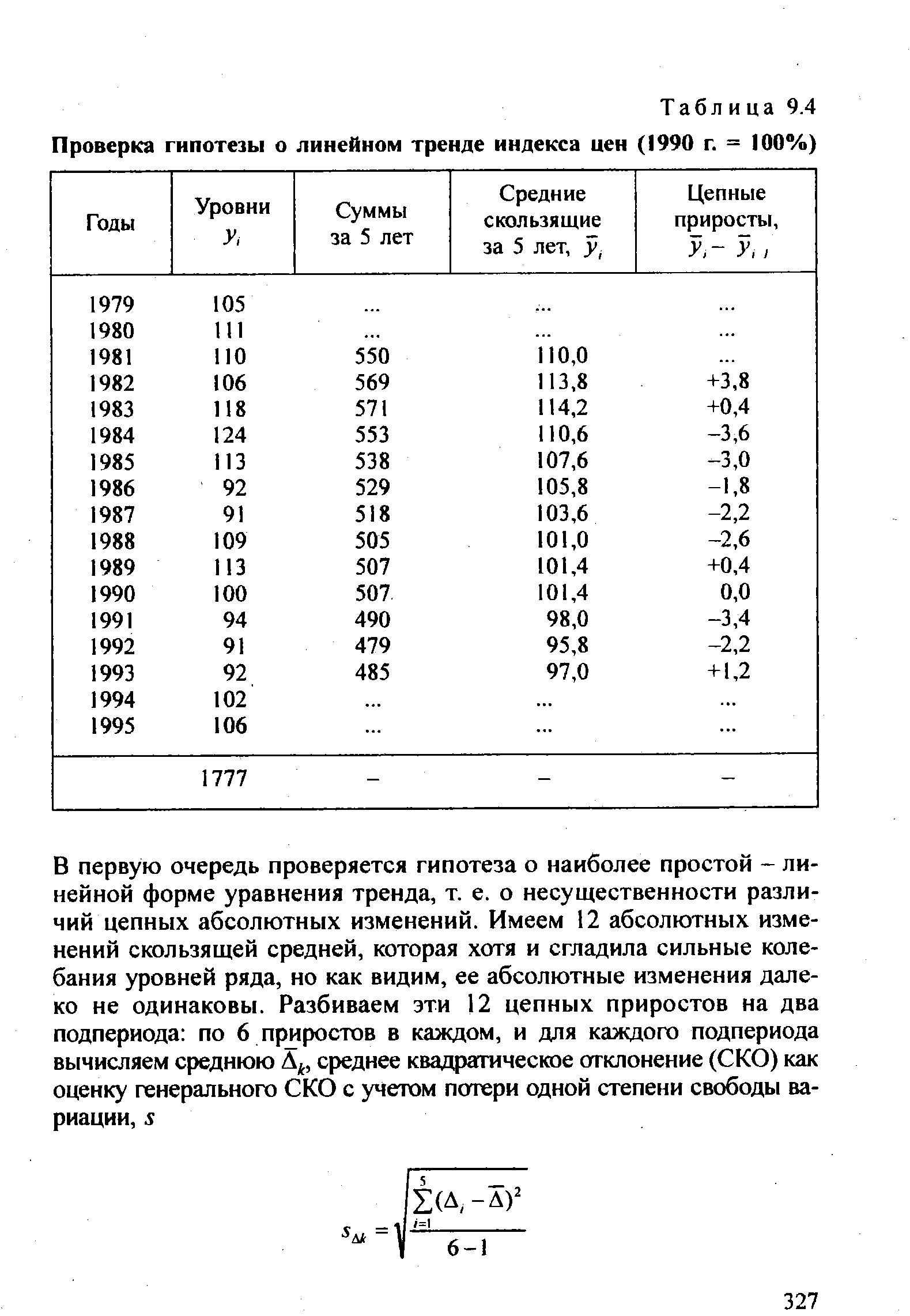 |
В формуле (9.33) суммирование от = -(л-1) 2до/ = (л- 1) 2 в целом формула (9.33) аналогична формуле для линейного тренда (9.29). [c.331]
Согласно формуле (9.29) параметры линейного тренда равны а = 1894/11 = 172,2 ц/га 2>Л= 486/110 = 4,418 ц/га. Уравнение линейного тренда имеет вид у = 172,2 + 4,418/, где ( = 0 в 1987 г. Это означает, что средний фактический и выравненный уровень, отнесенный к середине периода, т.е. к 1991 г., равен 172 ц с 1 га, а среднегодовой прирост составляет 4,418 ц/га в год. [c.332]
Поскольку по данным табл. 9.4, уже было установлено, что тренд имеет линейную форму, проводим расчет среднегодового абсолютного прироста, т. е. параметра Ъ уравнения линейного тренда сколь- [c.336]
Колеблемость умеренная, не сильная. Для сравнения приводим показатели (без расчета) по колебаниям урожайности картофеля, данные таблиц 9.1 и 9.5 - отклонение от линейного тренда s(t) = 14,38 ц с 1 га, v(t) = 8,35%. [c.342]
Средняя ошибка прогноза положения линейного тренда на год (момент) с номером tk вычисляется по формулам [c.358]
Для получения достаточно надежных границ прогноза положения тренда, скажем, с вероятностью 0,9 того, что ошибка будет не более указанной, следует среднюю ошибку умножить на величину /-критерия Стьюдента при указанной вероятности (или значимости 1 - 0,9 = 0,1) и при числе степеней свободы, равном, для линейного тренда, N- 2, т. е. 15. Эта величина равна 1,753. Получаем предельную с данной вероятностью ошибку [c.359]
Другим приемом измерения корреляции в рядах динамики может служить корреляция между теми из цепных показателей рядов, которые являются константами их трендов. При линейных трендах - это цепные абсолютные приросты. Вычислив их по исходным рядам динамики (axl, ayi), находим коэффициент корреляции между абсолютными изменениями по формуле (9.52) или, что более точно, по формуле (9.51), так как средние изменения не равны нулю в отличие от средних отклонений от трендов. Допустимость данного способа основана на том, что разность между соседними уровнями в основном состоит из колебаний, а доля тренда в них невелика, следовательно, искажение корреляции от тренда очень большое при кумулятивном эффекте на протяжении длительного периода, весьма мало - за каждый год в отдельности. Однако нужно помнить, что это справедливо лишь для рядов с с-показателем, существенно меньшим единицы. В нашем примере для ряда урожайности с-по-казатель равен 0,144, для себестоимости он равен 0,350. Коэффициент корреляции цепных абсолютных изменений составил 0,928, что очень близко к коэффициенту корреляции отклонений от трендов. [c.366]
В одном из предыдущих примеров мы рассмотрели прогноз по объему производства за два месяца некой компании из Дублина. Были получены оценки на 1997 год, при этом использовался линейный тренд и метод сложения. Прогнозные значения даны в тоннах [c.213]
Значения k для оценки доверительных интервалов прогноза относительно линейного тренда с вероятностью 0,8 [c.33]
Адаптивное моделирование линейного тренда с помощью экспоненциальных скользящих средних. [c.165]
Алгоритм вычисления параметров линейного тренда [c.169]
Вычислить в первом приближении параметры линейного тренда [c.169]
Определить окончательные значения параметров линейного тренда [c.169]
ЕМА ошибок могут ухудшить качество прогноза. В этом случае при расчете параметров линейного тренда нужно остановиться на шаге 2 этого алгоритма. [c.169]
Когда мы рассматриваем сектор рынка, соответствующий долгосрочным сделкам, вероятно, следует признать, что определяющее влияние на цены оказывают здесь такие экзогенные факторы, как обменные курсы и процентные ставки, показатели экономического роста, тенденции (тренды) цен и показателей прибыли. Поведение рынка здесь удовлетворительно описывается так называемой гипотезой эффективного рынка, согласно которой в каждый момент вся доступная информация о текущих и будущих событиях дисконтируется в текущие цены рынка, так что изменения цен бывают вызваны только поступающей свежей информацией. Напротив, в краткосрочной перспективе появляются новые возможности для прогнозов, связанные с учетом регулирования платежей, обратных связей и многочисленных технических и структурных факторов. Старые парадигмы финансовой науки типа модели случайного блуждания или гипотезы эффективного рынка внушают нам представление о том, что финансовые рынки склонны относительно плавно и разумно приспосабливаться к поступающей информации. В этом круге идей вполне убедительно выглядят описания поведения рынка на основе линейных зависимостей и законов обращения трендов (стационарности). Однако драматические обвалы рынка при отсутствии существенных изменений информации, резкие изменения условий доступа и сроков при пересечении компанией какого-то невидимого порога в кредитной сфере — все это проявления нелинейности. Действительность показывает, что поведение финансовых рынков едва ли может быть описано линейными трендами. [c.15]
LN — линейный тренд, сезонность не учитывается [c.68]
Если считать, что изменения цен, вопреки соображениям эффективности на продолжительных отрезках времени, определяются многочисленными и часто нелинейными обратными связями, то на основе теории хаоса можно построить улучшенные модели, описывающие влияние прошлого на настоящее (см. [213]-[216]). Драматические обвалы рынка при отсутствии существенных изменений информации, резкие изменения условий доступа и сроков при пересечении компанией какого-то невидимого порога в кредитной сфере — все это проявления нелинейности. Реальное поведение финансовых рынков, скорее, противоречит правилам обращения линейных трендов, чем подтверждает их. [c.74]
Метод последовательных разностей заключается в следующем если ряд содержит линейный тренд, тогда исходные данные заменяются первыми разностями [c.139]
Значения Лу не имеют четко выраженной тенденции, они варьируют вокруг среднего уровня, что означает наличие в ряде динамики линейного тренда (линейной тенденции). Аналогичный вывод можно сделать и по ряду х абсолютные приросты не имеют систематической направленности, они примерно стабильны, а следовательно, ряд характеризуется линейной тенденцией. [c.145]
Выпуск продукции, у —Линейный тренд [c.156]
Постройте уравнение линейного тренда и дайте интерпретацию его параметров, [c.163]
Определите коэффициент детерминации для линейного тренда. [c.163]
Уравнения линейных трендов [c.170]
Это привело к идее измерения корреляции не самих уровней х, иу а первых разностей Дх, = х, — , ,, 6у, — у, — у,.., (при линейных трендах). В общем случае было признано необходимым коррелировать отклонения от трендов (за вычетом циклической компоненты) Еу —у, — %, Ех = х, — %, (у,,% — тренды временных рядов). [c.19]
На графике рис. 5.3 наглядно видно наличие возрастающей тенденции. Возможно существование линейного тренда. [c.236]
Параметры линейного тренда можно интерпретировать так а — начальный уровень временного ряда в момент времени t = 0 b — средний за период абсолютный прирост уровней ряда. Применительно к данному временному ряду можно сказать, что темпы роста номинальной месячной заработной платы за 10 месяцев 1999 г. изменялись от уровня 82,66% со средним за месяц абсолютным приростом, равным 4,72 проц. пункта. Расчетные по линейному тренду значения уровней временного ряда определяются двумя способами. Во-первых, можно последовательно подставлять в найденное уравнение тренда значения / = 1, 2,..., л, т.е. [c.237]
Во-вторых, в соответствии с интерпретацией параметров линейного тренда каждый последующий уровень ряда есть сумма предыдущего уровня и среднего цепного абсолютного прироста, т. е. [c.238]
График линейного тренда приведен на рис. 5.3. [c.238]
Таким образом, начальный уровень ряда в соответствии с уравнением экспоненциального тренда составляет 83,96 (сравните с начальным уровнем 82,66 в линейном тренде), а средний цепной коэффициент роста — 1,046. Следовательно, можно сказать, что темпы роста номинальной месячной заработной платы за 10 месяцев 1999 г. изменялись от уровня 83,96% со средним за месяц цепным темпом роста, равным 104,6%. Иными словами, средний за месяц цепной темп прироста временного ряда составил 4,6%. [c.238]
Шаг 4. Определим компоненту Т данной модели. Для этого проведем аналитическое выравнивание ряда (Т+ Е) с помощью линейного тренда. Результаты аналитического выравнивания следующие [c.244]
Такой переход позволяет определить знак изменения курса валюты, что достаточно для достижения прибыли от операций с ней. При наличии у временного ряда линейного тренда могут быть применены и другие методы адаптивного прогнозирования Брауна, Хольта и Тей-ла-Вейджа. [c.676]
Рассчитанные по уравнениям трендов уровни записаны в трех последних графах табл. 9.5. Как видно по этим данным, расчетные значения уровней по всем трем видам трендов различаются ненамного, так как и ускорение параболы, и темп роста экспоненты невелики. Существенное отличие имеет парабола - рост уровней с 1995 г. прекращается, в то время как при линейном тренде уровни растут и далее, а при экспоненте их рост ускоряется. Поэтому для прогнозов на будущее эти три тренда неравноправны при экстраполяции параболы на будущие годы уровни резко разойдутся с прямой и экспонентой, что видно из табл. 9.6. В этой таблице представлена распечатка решения на ПЭВМ по программе Statgraphi s тех же трех трендов. Отличие их свободных членов от приведенных выше объясняется тем, что программа нумерует года не от середины, а от начала, так что свободные члены трендов относятся к 1986 г., для которого / = 0. Уравнение экспоненты на распечатке оставлено в логарифмированном виде. Прогноз сделан на 5 лет вперед, т.е. до 2001 г.. При изменении начала координат (отсчета времени) в уравнении параболы меняется и средний абсолютный прирост, параметр Ъ, так как в результате отрицательного ускорения [c.332]
Для определения параметров линейного тренда по методу наименьших квадратов используется статистическая функция ЛИНЕЙН, для определения экспоненциального тренда -ЛГРФПРИБЛ. Порядок вычисления был рассмотрен в 1-м разделе практикума. В качестве зависимой переменной в данном примере выступает время (г = 1, 2,. .., л). Приведем результаты вычисления функций ЛИНЕЙН и ЛГРФПРИБЛ (рис. 4.2 и 4.3). [c.151]
