Данная модель обладает интересным и далеко идущим следствием с точки зрения повторения и организации крахов во времени. Действительно, мы видим, что каждый раз, когда случайные блуждания приближаются к выбранной постоянной величине W , цена пузыря взмывает вверх, и, согласно условию отсутствия арбитража совместно с рациональными ожиданиями, это подразумевает под собой то, что рынок входит в "опасные воды" с приближающимся крахом. Модель случайных блужданий обеспечивает нас очень точным предсказанием времени ожидания между успешными приближениями к критическому значению We, то есть между успешными пузырями. Распределение данных сроков ожидания считается очень широким степенным распределением [394], настолько широким, что среднее время ожидания является [c.171]
Когда мы рассматриваем сектор рынка, соответствующий долгосрочным сделкам, вероятно, следует признать, что определяющее влияние на цены оказывают здесь такие экзогенные факторы, как обменные курсы и процентные ставки, показатели экономического роста, тенденции (тренды) цен и показателей прибыли. Поведение рынка здесь удовлетворительно описывается так называемой гипотезой эффективного рынка, согласно которой в каждый момент вся доступная информация о текущих и будущих событиях дисконтируется в текущие цены рынка, так что изменения цен бывают вызваны только поступающей свежей информацией. Напротив, в краткосрочной перспективе появляются новые возможности для прогнозов, связанные с учетом регулирования платежей, обратных связей и многочисленных технических и структурных факторов. Старые парадигмы финансовой науки типа модели случайного блуждания или гипотезы эффективного рынка внушают нам представление о том, что финансовые рынки склонны относительно плавно и разумно приспосабливаться к поступающей информации. В этом круге идей вполне убедительно выглядят описания поведения рынка на основе линейных зависимостей и законов обращения трендов (стационарности). Однако драматические обвалы рынка при отсутствии существенных изменений информации, резкие изменения условий доступа и сроков при пересечении компанией какого-то невидимого порога в кредитной сфере — все это проявления нелинейности. Действительность показывает, что поведение финансовых рынков едва ли может быть описано линейными трендами. [c.15]
Устоявшиеся парадигмы финансовой науки, такие, как модель случайного блуждания и гипотеза эффективного рынка, предполагают, что финансовые рынки реагируют на информацию рационально и плавно. В этом случае едва ли можно придумать что-то лучше линейных связей и стационарного (обращающего тренды) поведения. [c.75]
В общем, статистический анализ требует нормального распределения или известной колоколообразной кривой. Известно, что рыночные прибыли не подвержены нормальному распределению, но эта информация была сглажена или рационализирована за многие годы, чтобы сохранить критическое предположение о том, что рыночные прибыли следуют модели случайных блужданий. [c.30]
В теории финансового инвестирования нет концепции, которая имела бы такую широкую проверку и так мало доверия к себе, как эффективные рынки . Помимо всего эта концепция является краеугольным камнем количественной теории рынка капитала, и последние тридцать с лишним лет исследований были полностью ей подчинены. В действительности гипотеза эффективного рынка (ЕМН) уходит корнями в начало века. Она выполняет одну первейшую функцию оправдать использование вероятностных расчетов в анализе рынков капитала. Но если рынки являются нелинейными динамическими системами, то тогда использование стандартного статистического анализа может привести к ошибочным результатам, особенно если в основе лежит модель случайных блужданий. Поэтому становится важным пересмотр тех предпосылок, которые стоят во главе угла нынешней теории рынков капитала. [c.28]
Модель случайного блуждания [c.36]
Ранее ( 2а, гл. I) отмечалось, что Л. Башелье был, безусловно, первым, кто для описания динамики цен акций обратился (см. [12]) к моделям "случайных блужданий и их предельным образованиям" которые, говоря современным языком, есть не что иное, как броуновское движение. [c.417]
Если отвлечься от математических обозначений, то модель случайного блуждания утверждает следующее движение фондового рынка в целом (и цен отдельных инструментов, обращающихся на нем) непредсказуемо. Цена фондового актива в соответствии с этой моделью изменяется абсолютно случайно. Инвестор равновероятно может ожидать падения или роста зав- [c.187]
Естественно, подобный вывод не осчастливил профессионалов фондового рынка. Ведь если модель случайного блуждания работает на практике, то это означает, что их работа абсолютно бесполезна — даже подслеповатая обезьяна сможет провести операцию с ценными бумагами, которая по показателям прибыльности будет не хуже (а скорее всего, даже лучше) операции, проведенной профессиональным участником. Абсурд — сказали профессионалы и вернулись к трендам. [c.189]
Годом великого перелома стал 1965-й. В этом году публикуется работа Пола Самуэльсона Доказательство случайного изменения рационально ожидаемых цен 1. Используя инструменты микроэкономического анализа, Самуэльсон показал, что на рынке, где присутствует совершенная конкуренция, динамика цен должна подчиняться модели случайного блуждания, а значит, должна быть непредсказуемой. [c.189]
Единственное практическое следствие теории заключается в том, что если вся информация, относящаяся к ценным бумагам, в любой момент времени полностью отражается рыночными ценами, то динамика цен фондовых активов, обращающихся на подобном рынке, подчиняется модели случайного блуждания. Если же динамика цен подчиняется модели случайного блуждания (т. е. непредсказуема), то ни один оператор рынка не может получить доход от проведения операций с ценными бумагами, который отличался бы от нормального. Нормальный доход — это доходность рыночного индекса. [c.193]
Необходимо рассмотреть еще один момент, который может вызвать некоторые вопросы. Почему при условии, что все операторы рынка одинаково полно информированы, никто не может сказать ничего определенного по поводу будущих значений цен фондовых активов Другими словами, почему динамика цен подчиняется модели случайного блуждания, в то время как операторы рынка имеют доступ ко всей информации [c.195]
Именно поэтому динамика цен будет подчиняться модели случайного блуждания — на эффективном рынке операторы равновероятно могут ожидать, что их прогнозы завышены или занижены относительно реальных будущих значений цен. [c.196]
Однако значение теории эффективного рынка вовсе не в том, что она подтверждает модель случайного блуждания, а в том, что она четко устанавливает необходимое условие, при котором цены действительно будут вести себя так, как если бы они подчинялись модели случайного блуждания. [c.196]
Более того, если в действительности в процессе порождения данных /3=1, так что мы имеем дело с популярной моделью случайного блуждания (выходящего из нуля), [c.6]
Это соответствует модели случайного блуждания со сносом [c.128]
Неправильный выбор оцениваемой статистической модели может существенно отразиться на мощности критерия Дики - Фуллера. Например, если наблюдаемый ряд порождается моделью случайного блуждания со сносом, а статистические выводы производятся на основании результатов оценивания статистической модели без включения в ее правую часть трендовой составляющей, то тогда мощность критерия, основанная на статистике tp, стремится к нулю с возрастанием количества наблюдений [c.135]
Как практикующий технический аналитик и член Ассоциации технических аналитиков рынка, я естественно не соглашаюсь с аргументами случайных блужданий. Но я также спорю и с аргументами технических аналитиков. Я искренне соглашаюсь с моими товарищами, что смехотворно спорить, что нет никакого способа предсказать будущие цены акции, основываясь на изучении прошлых моделей цен и объема. Но в то же самое время, я настоятельно полагаю, что диаграмма не "сообщает все", поскольку чистый анализ диаграммы не будет показывать компоненту настроения, которая является жизненно важной для успешного предсказания будущих цен акции. [c.242]
Прочитав эти строки, большинство читателей, вероятно, будут весьма разочарованы зачем же тратить время на изучение рынка акций, если игра на бирже в принципе приводит к разорению Автор, однако, просит набраться терпения и не прекращать чтения книги — все не так плохо, как сейчас может показаться. Рассмотренные методы расчетов нам пригодятся — их широко применяют в аналитической работе, так как они дают удобные модели, соответствующие случайному характеру биржевых процессов. Но они не отражают всей сложной природы акций и их движения, в котором есть не только случайности, но и закономерности. Строго говоря, в целом цены акций не подчиняются законам случайных блужданий, и мы будем непрерывно демонстрировать это на протяжении всей книги. Если даже они случайно блуждают в течение короткого [c.51]
Общепринято, среди создателей моделей финансовых рынков, представлять вариацию цен в течение элементарного временного периода как результат воздействия двух факторов детерминированного мгновенного приращения и случайного приращения. Первый фактор включает в себя компенсацию за предполагаемый риск, а также действие на цену таких причин, как подражание и стадность. Второй фактор включает в себя шумовой компонент ценовой динамики с амплитудой, называемой волатильностью. Волатильность также может представлять собой систематический компонент, управляемый подражанием, а также многими другими факторами. Если первый фактор формирования цены отсутствует, а волатильность постоянна, то второй член сам по себе создает траектории случайных блужданий, описанные в главе 2. Введение в модель вездесущей нелинейной зависимости волатильности и определенного мгновенного приращения от прошлых значений волатильности и доходностей дает нам великое множество всевозможных траекторий. Здесь нам интересны многочисленные возможные механизмы, ведущие к нелинейной положительной обратной связи цен с самими собой. Например, неточная информация и перенос риска с инвесторов на кредитуемые банки могут заставить инвесторов поднимать цены спроса на актив в большей степени, чем они хотели бы заплатить в случае, если бы полностью несли все потенциальные убытки [3]. Мы вернемся к интуитивному описанию других механизмов в главах 7 и 8. [c.168]
Рис. 59 показывает типичную траекторию пузырной компоненты цены, сгенерированной моделью с нелинейной положительной обратной связью [396], начиная с некоторой начальной величины вверх вплоть до того времени, когда цены начинают взмывать. Самый простой вариант данной модели состоит из цены пузыря B(t), являющейся инверсной степенью случайных блужданий W(t), в следующем смысле. Начиная с B(0)=W(0)=0, в начале времени, когда случайные блуждания приближаются к некой величине W , которая здесь равна 1, B(t) увеличивается и наоборот. В частности, когда W(t) приближается к 1, B(t) раздувается и достигает сингулярности во время t , когда случайные блуждания пересекают 1. Данный процесс в случайной области распространяет такие сингулярности конечного времени, описанные ранее в данной главе, что монотонно растущий процесс с кульминацией в критическое время t заменяется случайными блужданиями, бродящими вверх и вниз, прежде, чем они в конечном счете достигнут критического уровня. Данный нелинейный положительный раздутый [c.169]
Определение коэффициента угрозы краха. Симуляция с использованием компьютерной программы идет следующим образом. Во-первых, мы выбираем дискретизацию времени с шагом St. Затем, зная величину случайных блужданий W(t-St) и цену B(t-8t) в предшествующее время t-dt, мы выводим W(t), прибавляя приращение, взятое из центрированного гауссова распределения с вариацией St. Отсюда мы выводим цену B(t), взяв величину, обратную (W -W(t))a, где - положительный показатель степени, определенный в модели. Затем мы выражаем, при условиях отсутствия арбитража и рациональных ожиданиях, вероятность h(t) возникновения краха во время следующего временного этапа, где h(t) - коэффициент угрозы краха. Мы сравниваем данную вероятность со случайным числом гаи, равномерно выбранным в интервале [0,1] и запускаем механизм краха, если ran < h(t)St. В данном случае цена B(t) меняется на B(t)(l-K), где к взято из предварительно выбранного распределения. Например, спад к при крахе может быть зафиксирован на уровне, скажем, 20%. Слишком прямолинейно сводить это к арбитражному распределению скачков. После краха динамика продолжается с бесконечно малым приращением, как и раньше, начиная с этого нового значения для времени t, после соответствующего переноса W(t), чтобы обеспечить непрерывность цен. Если ran > h(t)St, краха не происходит и динамика повторится на следующем временном шаге. [c.171]
Вместо движения с постоянной скоростью, когда значение текуща координаты увеличивается пропорционально времени, частица, движени которой описывается моделью случайного блуждания, совершае хаотические движения, в котором типичная флуктуация её положени увеличивается медленнее, чем по линейному, во времени, закону, фактически пропорционально корню квадратному от времени. Результат замедлени [c.52]
Посмотрим, следует ли такой прогноз из анализа данных. Основополагающая идея состоит в том, что приращения на дневном масштабе есть сумма приращений в каждую минуту этого дня. Соответственно, месячные приращения представляют собой сумму дневных приращений этого месяца. Так как динамика приращении основана на модели случайных блужданий, то ранее рассмотренный закон "квадратного корня" должен выполняться. Дня подтверждения, рассмотрим Рис. 13, где типичная амплитуда изменении на 1-мнутном временном масштабе составляет около 0.04% (причем, это справедливо для большинства значений). На Рис. 14, такие же визуальные оценки могут привести к типичной амплитуде флуктуации, равной около 1%. Теперь 1% разделим на 0.04% и получим значение 25, которое достаточно близко к корню квадратному равному 20.25 из числа минут торгового дня (обычно 410). Подобным образом, оценим из Рис. 15 типичную амплитуду изменений на месячном интервале равную около 5%. Отношение месячного значения равного 5% к дневному значению равному 1% эквивалентно 5, что совсем близко к корню квадратному из числа торговых дней в месяце, обычно это 20-24 дня. Теория случайных блужданий, таким образом, достаточно адекватно описывает типичные изменения на рынке акций во времени и на разных временных масштабах. Однако, она не дает объяснения большим приращениям, не являющимися типичными, как это можно увидеть на Рис. 14 и Рис. 15. [c.53]
Однако, любой, кто пытался вкладывать капитал на рынке акции, знает, что трудность состоит в том, что тренды и развороты тренда происходят на всех масштабах времени. Рис. 45 иллюстрирует это наблюдение построением, основанным на вставках последовательностей трендов и разворотов трендов на всех масштабах. Это геометрическое построение, которое улучшает и обобщает модель случайного блуждания, весьма близко воспроизводит структуру ценовых траекторий, показанных в главе 2. Эти инвариантные к масштабу модели построены из блоков трендов "вверх-вниз", которые могут наблюдаться и воспроизводить себя на всех масштабах и почти повсюду. Эти модели принадлежат геометрии фракталов [284], грубой или фрагментированной геометрической форме, которая может быть разделена на части, каждая из которых (по крайней мере, приблизительно) является уменьшенной копией целого. Концепция фракталов, представленная Мандель-бротом (Mandelbrot), охватывает грубые, ломаные и нерегулярные характеристики многих явлений в природе, присутствующие во всех масштабах. Мы вернемся к этому построению, показанному на Рис. 45, и его значениям в главе 6. [c.127]
Наши коллеги в финансовых подразделениях далеко не всегда приветствовали такой либеральный и неструктурный в смысле модели подход к проблеме. Примерно до 1994 года консервативные эко-нометристы отвергали саму идею о том, что нейронные сети могут быть средством моделирования. Сетевые методы подвергались насмешкам из-за того, что они устроены как черный ящик , а также из-за наличия обучающих параметров, подбор которых производится практически на глаз . В самом деле, разве профессор X. Уайт не доказал со всей определенностью,4 что в задаче прогнозирования дохода по акциям IBM нейронные сети дают худшие результаты, чем модель случайного блуждания [c.6]
Фамэ (Fama, 1965a) окончательно формализовал эти наблюдения в виде гипотезы эффективного рынка (ЕМН), которая утверждает, что рынок является мартингалом, или справедливой игрой это означает, что информация не может быть использована для выигрыша на торговой площадке. ЕМН подобна предположению 5 Осборна. В ее чистой форме ЕМН не требует независимости во времени или принятия только IID наблюдений. Однако модель случайного блуждания исходит из этих предположений. Если прибыли случайны, [c.34]
Этот краткий обзор показывает, что по поводу ЕМН возникли серьезные вопросы. В главе 2 мы видели, что ЕМН была необходима для того, чтобы оправдать предположение о случайном блуждании цен. Следовательно, модель случайного блуждания не находит себе места без ЕМН, хотя это отношение отнюдь не обратимо. Случайное блуждание было необходимо для применения статистического анализа к временным рядам ценовых изменений. Статистический анализ был необходим хотя бы только для того, чтобы теория портфеля была применима в реальности. Без нормального распределения огромное число теоретических и эмпирических работ ставится ПГ1П, погтрпг Мы также видели, что традиционный компромисс между риском и прибылью не всегда имеет место. [c.53]
В 1953 г. на очередном собрании Королевского статистического общества в Лондоне выдающимся статистиком Морисом Кен-даллом была представлена работа Анализ экономических временных рядов . В своей работе Кендалл попытался выявить цикличность поведения цен акций английских компаний и товарных цен (всего было использовано 22 временных ряда). К своему удивлению, Кендалл обнаружил, что нет никакой возможности вывести регулярные циклы динамики цен акций, так как каждая серия казалась построенной таким образом, как если бы Его Величество Случай извлекал случайным образом число. .. и добавлял его к текущей цене, для того чтобы определить цену в следующий момент . То, что обнаружил Кендалл, теперь принято называть моделью случайного блуждания [random walk model]. [c.187]
Атака теоретиков возобновилась в 1959 г., когда уже другой статистик — Гарри Роберте продемонстировал, что динамика временного ряда, искусственно сгенерированного датчиком случайных чисел, неотличима от динамики временного ряда, содержащего цены американских акций2. В заключение своей работы Роберте писал Основная цель данной работы — привлечь внимание финансовых аналитиков к эмпирическим результатам, которые по той или иной причине игнорировалась в прошлом, и указать некоторые методологические приложения этих результатов для изучения ценных бумаг . Судя по всему, под эмпирическими результатами Роберте имел в виду практическую значимость модели случайного блуждания, а под методологическими приложениями — непредсказуемость будущих цен фондовых активов. [c.188]
Во-вторых, и это более важно, если предположить существование на рынке долгосрочных аномалий, которые уже не могут быть описаны моделью случайного блуждания (другими словами, быть случайными), то рынок уже точно не может быть эффективным. Но Фама считает и показывает, что эти долгосрочные аномалии крайне чувствительны к методологии, используемой исследователем. Эти аномалии становятся незначительными или вообще исчезают, если применять иные модели ожидаемой (нормальной) доходности или если при исследовании применять иные статистические техники. Таким образом, заключает Фама, большинство долгосрочных аномалий доходностей может быть спокойно отнесено к игре чистого случая. [c.255]
Принимая во внимание все изложенное ранее, здесь очевидна необходимость различения модели случайного блуждания со сносом и процесса, стационарного относительно линейного тренда. Последуем процедуре Доладо и др. [c.144]
Вместо того, чтобы слушать теоретиков, я пошел на рынок, чтобы увидеть, что он может мне показать. Я задал вышеупомянутые вопросы и многие другие, чтобы понять, существует ли зависимость одного дня от другого или от какой-то ценовой фигуры или прошлого ценового поведения, которое последовательно влияет на завтрашнюю цену, заставляя ее двигаться за пределы критической точки случайного блуждания. Ответ был ясен рынок не соответствует модели Кутнера. Таблицы 6.1 и 6.2 доказывают мою точку зрения. [c.100]
| Рис. 19. Синтетически случайная рыночная цена (или позиции случайного блуждания полученная бросанием "компьютерной монеты" для определения направления изменени цены вверх или вниз. В этой модели шаг или интервал приращения имеет случайный знак амплитуду, распределенную согласно, так называемому распределению Гаусса с 11 стандартным отклонением. Те же самые приращения использованы при построении Рис. К синтетическая траектория, построенная здесь, таким образом, есть не что иное, ка нарастающая сумма приращений, представленных на Рис. 16. | 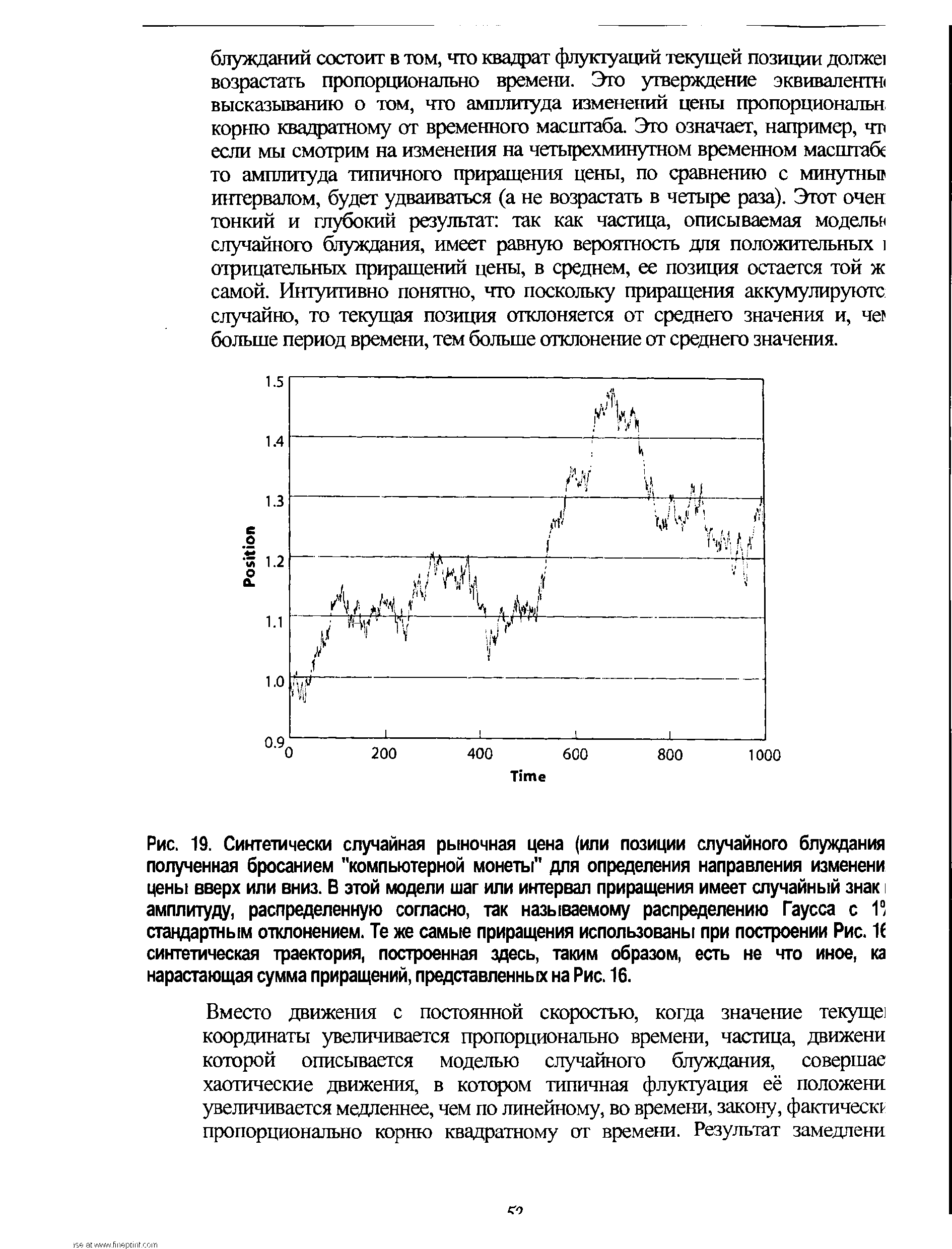 |
Данное свидетельство, вместе с тем фактом, что пузыри не должны все время проникать в динамику цены, подталкивает нас к следующему естественному расширению модели. При самом простом и экономном расширении, мы можем предположить, что могут произойти только два режима пузырь и нормальный. Режим пузыря следует за предыдущим определением модели и прерывается крахами, случающимися с коэффициентом угрозы, управляемым уровнем цены. Нормальным режимом могут быть, например, стандартные случайные блуждания в рыночной модели с постоянным маленьким дрейфом и волатильностью. Переключения между режимами предполагаются совершенно случайными. Эта динамическая и очень простая модель обретает по существу все традиционно наблюдаемые факты эмпирических цен, то есть отсутствие связи с волатильностью, длинный хвост распределений приращений, очевидную фрактальность и мульти-фрактальность, наличие резких плоских пиков в структуре просто ценовых пиков. Помимо этого, модель предсказывает то, что периоды пузырей связаны с нестационарными корреляциями растущей волатильности и мы подтверждаем это анализом эмпирических данных. Об этом мы поговорим далее, в наших эмпирических главах 7-10. Предполагается, что очевидная долгосрочная корреляция волатильности является результатом [c.172]
Смотреть страницы где упоминается термин Модель случайного блуждания
: [c.53] [c.988] [c.93] [c.5] [c.49] [c.135] [c.255] [c.140] [c.988] [c.51] [c.172] [c.173]Смотреть главы в:
Трейдинг Дополнительное измерение принятия решений -> Модель случайного блуждания
