Модель финансового рынка 49 [c.49]
Простая модель финансового рынка. Если при достаточно низких ценах покупатели испытывают трудности с финансированием, то характер обратной связи будет нелинейным, что можно учесть, возводя уровень цены в степень, большую единицы. [c.117]
Общепринято, среди создателей моделей финансовых рынков, представлять вариацию цен в течение элементарного временного периода как результат воздействия двух факторов детерминированного мгновенного приращения и случайного приращения. Первый фактор включает в себя компенсацию за предполагаемый риск, а также действие на цену таких причин, как подражание и стадность. Второй фактор включает в себя шумовой компонент ценовой динамики с амплитудой, называемой волатильностью. Волатильность также может представлять собой систематический компонент, управляемый подражанием, а также многими другими факторами. Если первый фактор формирования цены отсутствует, а волатильность постоянна, то второй член сам по себе создает траектории случайных блужданий, описанные в главе 2. Введение в модель вездесущей нелинейной зависимости волатильности и определенного мгновенного приращения от прошлых значений волатильности и доходностей дает нам великое множество всевозможных траекторий. Здесь нам интересны многочисленные возможные механизмы, ведущие к нелинейной положительной обратной связи цен с самими собой. Например, неточная информация и перенос риска с инвесторов на кредитуемые банки могут заставить инвесторов поднимать цены спроса на актив в большей степени, чем они хотели бы заплатить в случае, если бы полностью несли все потенциальные убытки [3]. Мы вернемся к интуитивному описанию других механизмов в главах 7 и 8. [c.168]
Рассмотрим простую модель финансового рынка, в которой для продавцов привлекательна высокая, а для покупателей — низкая рыночная цена. Если при достаточно низких ценах покупатели испытывают трудности с финансированием, то характер обратной связи будет нелинейным. Этот эффект можно учесть, возводя уровень цены в степень, большую единицы, например, в квадрат. Если коэффициенты обратной связи для продавца обозначить /5, а для [c.74]
В основе всего изложения лежит концепция арбитража, которая помогает среди разнообразных моделей финансовых рынков выделить, прежде всего, те - "справедливо" устроенные, на которых отсутствуют арбитражные возможности. [c.540]
В расширенном варианте "второй фундаментальной теоремы" описывается также и структура цен в полных безарбитражных моделях финансовых рынков. [c.540]
Разработкой четких описательных моделей финансовых рынков и их участников и занимаются поведенческие финансы. Это интересует и нас. [c.18]
Синтезированная таким образом стохастическая дифференциальная модель финансового рынка по своей математической форме будет полностью удовлетворять требованиям, накладываемым теорией оптимального управления , и будет адекватно описывать статистическую природу протекающих на финансовом рынке процессов. [c.162]
Ниже достаточно подробно рассматриваются этапы синтеза дифференциальной стохастической модели финансового рынка и моделей обращающихся на нём финансовых инструментов. [c.162]
Математические модели финансового рынка в виде дифференциальных и разностных уравнений [c.167]
С учётом того, что поведение финансового рынка в динамике может быть описано с помощью дифференциальных (для дискретного времени - разностных) уравнений формирующих фильтров, возбуждаемых в правой части случайными процессами липа белого шума, приходим к тому, что модель финансового рынка в точности соответствует понятию стохастической дифференциальной системы[4]. [c.168]
Математическая модель финансового рынка в непрерывном времени [c.168]
Математическая модель финансового рынка может быть представлена в виде векторно-матричного дифференциального уравнения вида [c.168]
Учитывая всё сказанное выше о модели финансового рынка как стохастической дифференциальной системы, на него полностью распространяются все результаты теории стохастических дифференциальных систем[4]. Поэтому ниже приводится[4] сводка окончательных результатов в виде дифференциальных уравнений для моментов векторного случайного процесса [c.172]
Ниже на рис. 7.4 представлена математическая модель финансового рынка в непрерывном времени в виде формирующего фильтра случайного процесса X(t) в соответствии с дифференциальным уравнением (7.3.5). [c.174]
| Рис. 7.4 Блок-схема математической модели финансового рынка в непрерывном времени. | 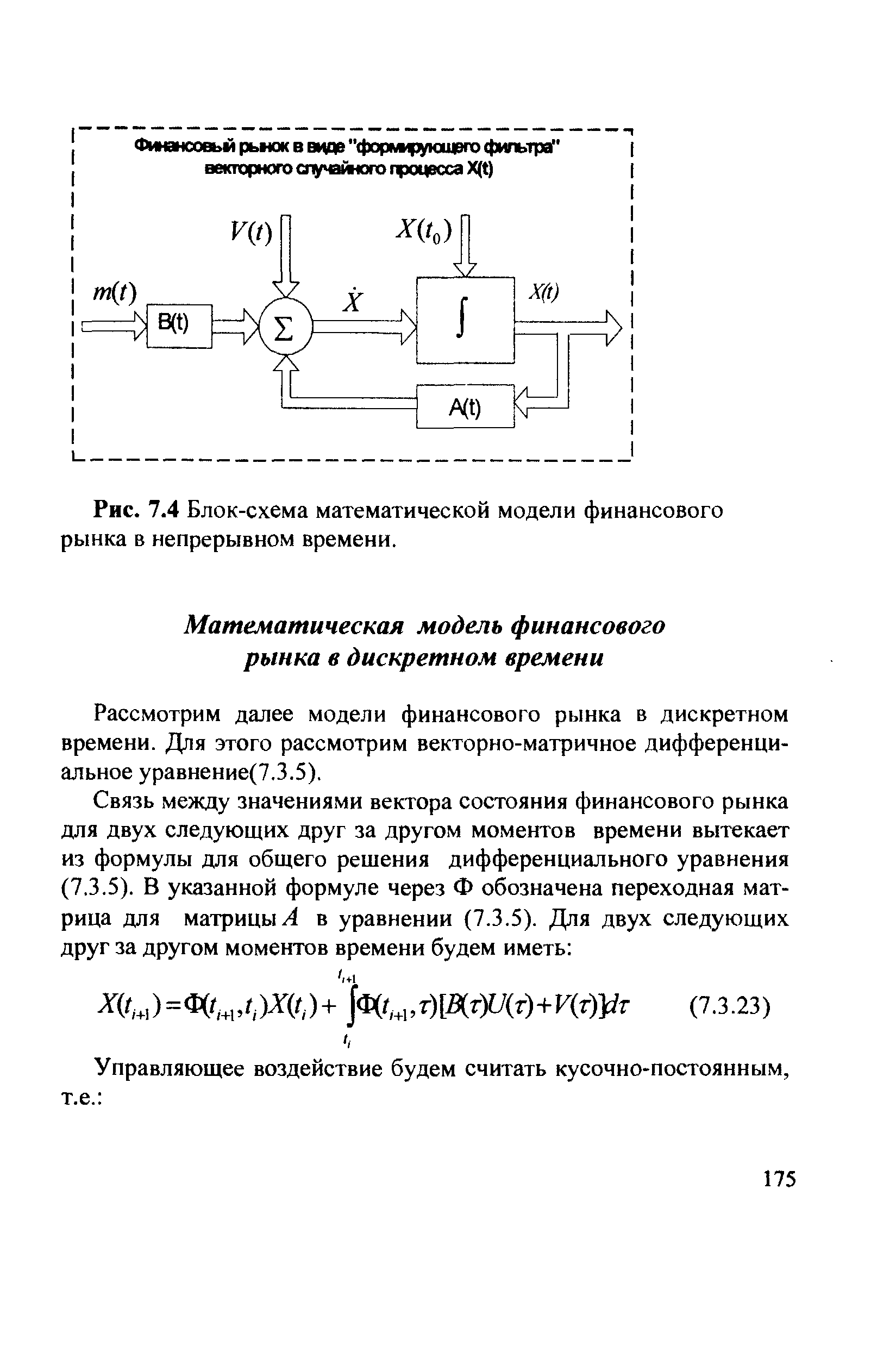 |
Из полученных соотношений (7.3.23-7.3.28) вытекает дискретный вариант непрерывной модели финансового рынка в виде [c.176]
Синтез конкретных моделей финансового рынка [c.177]
При построении математической модели финансового рынка [1] будем полагать что [c.177]
Подобный подход открывает путь построения статистической модели финансового рынка и последующего использования математических методов теории оптимального управления для синтеза оптимальных стратегий инвестирования и биржевых спекуляций. [c.177]
Для простоты изложения мы ограничимся рассмотрением лишь линейной модели финансового рынка и обращающихся на нём инструментов в виде систем линейных дифференциальных и разностных уравнений. Синтез математической модели будем осуществлять в рамках корреляционной теории случайных процессов. [c.178]
Путь построения конкретных математических моделей финансового рынка может состоять в следующем [1] [c.178]
При построении соответствующих моделей финансового рынка и обращающихся на нём финансовых инструментов наиболее удобно в качестве случайных координат вектора состояния рынка рассматривать ЭФФЕКТИВНОСТИ обращающихся на нём инструментов, а также возможно их производные до 2-го порядка включительно. Понятие эффективности (доходности) финансовых инструментов мы ранее подробно рассматривали в разделе 6 книги. Здесь мы ограничимся напоминанием основных моментов. [c.178]
Как отмечалось нами ранее в разделе 7.2.2, в рамках корреляционной теории случайных процессов математической моделью финансового рынка может служить векторно-матричное дифференциальное уравнение формирующего фильтра в виде [c.182]
Структурная схема математической модели финансового рынка в дискретном времени, с учётом разностного уравнения (7.3.36), представлена ниже на рис. 7.7 в виде блок-схемы [c.184]
| Рис. 7.7. Математическая модель финансового рынка в дискретном времени в виде формирующего фильтра векторного случайного процесса. | 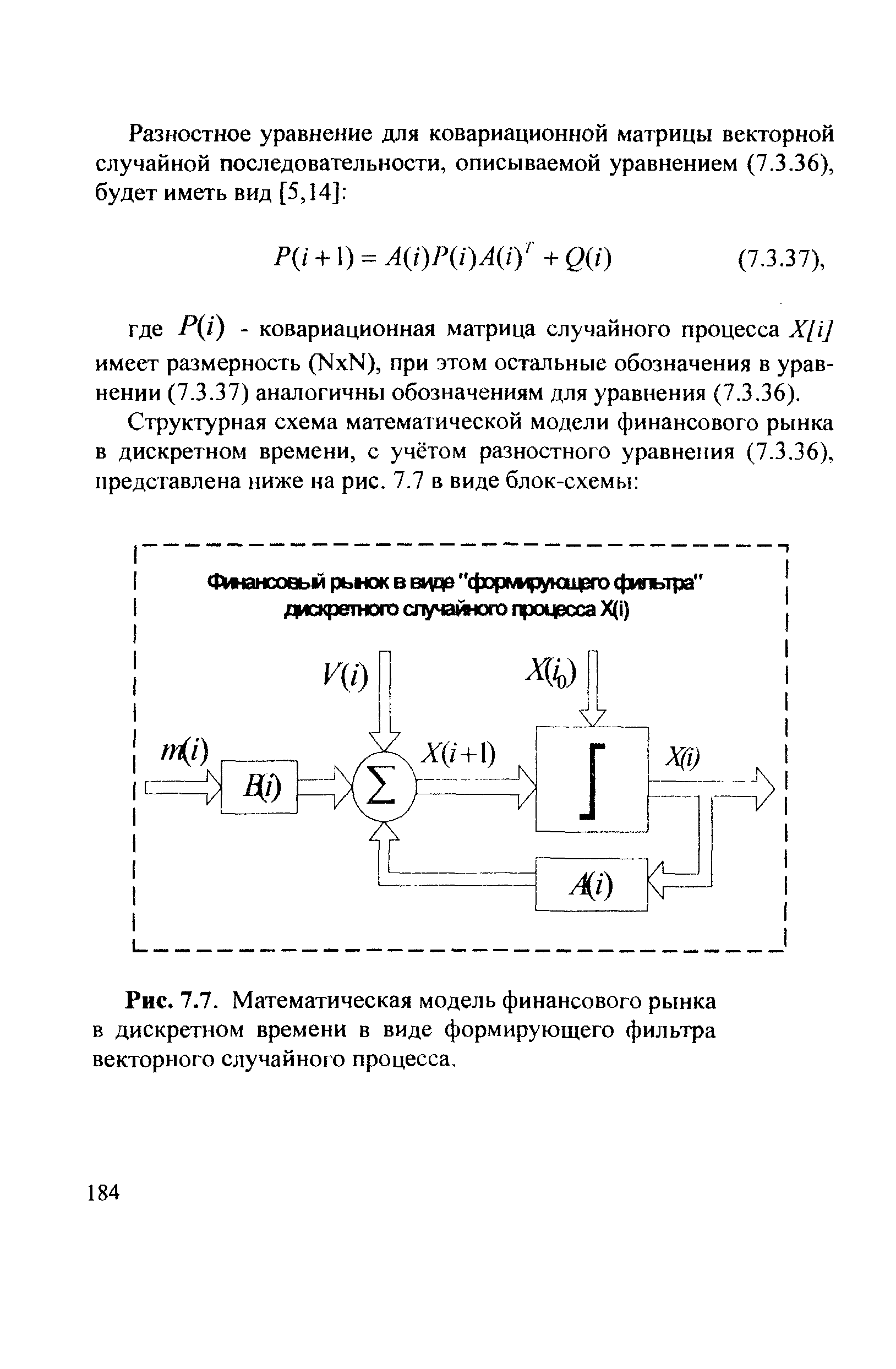 |
Хорошо известно[5,6], что оптимальным по критерию минимума среднеквадратической ошибки оценивания состояния ( текущего , прошлого и будущего ) динамической системы является алгоритм, называемый фильтром Р. Калмана. Все любые другие алгоритмы оценивания по точности могут лишь приближаться к точности оценивания, которую обеспечивает фильтр Калмана. Потенциально возможная точность оценивания, достигаемая указанным фильтром, обеспечивается благодаря тому, что структура и параметры указанного алгоритма предварительно настраиваются на статистический портрет оцениваемой динамической системы. Именно поэтому необходимо проводить предварительные статистические исследования финансового рынка, чтобы получить адекватную рынку математическую модель в виде системы дифференциальных (разностных) уравнений, и уже затем настроить соответствующий фильтр Калмана на полученную математическую модель финансового рынка. [c.196]
Модуль синтеза математической модели финансового рынка На основе известных соотношений[4,25] между корреляционными функциями случайных процессов и дифференциальными (разностными) уравнениями идентифицируются векторно-матричные дифференциальные (разностные) уравнения, описывающие статистическую динамику финансового рынка. [c.228]
Определенность - это когда известно все необходимое для расчетов. Неопределенность (отрицание определенности) приводит к неоднозначным результатам, что и есть риск. В условиях неопределенности у финансовых операции появляется еще одна характеристика - рискованность. Риску посвящены гл. 10-12, да и в остальных это понятие - одно из центральных. В гл. 9 изложены некоторые изменения в финансовых расчетах, проводимых в условиях неполной определенности. В гл. 13 рассмотрена биномиальная модель ценообразования на финансовом рынке и некоторые ее модификации. Гл. 14 посвящена опционам - производным финансовым инструментам, играющим сегодня наиболее важную роль на финансовом рынке. В гл. 15,16 изложена теория оптимального портфеля, в гл. 17 коротко описаны некоторые модели финансовых рынков. Дополнение к ч. 2 содержит изложение теории полезности и отношения ЛЦР (инвесторов) к риску. [c.67]
Замечание. Описанные модели финансовых рынков частично перекрывают друг друга, так что каких-то очень четких границ каждой модели не существует. Можно лишь выделить некоторые ключевые положения этих моделей [c.150]
Какой-либо самой лучшей, общепризнанной модели финансового рынка не существует. [c.150]
Познакомившись с важнейшими финансовыми учреждениями и их макроэкономической ролью, мы можем перейти к построению модели финансовых рынков. Цель построения такой модели — объяснение роли финансовых рынков в регулировании движения средств, направляемых на сбережения и инвестиции, и анализ влияния различных типов государственной политики на процессы сбережения и инвестирования. [c.546]
К сожалению, в существующих и наиболее распространенных сегодня региональных экономических моделях отсутствуют разработанные и научно обоснованные блоки, посвященные денежным и финансовым рынкам Отчасти это связано с отсутствием систематизированной информации о денежных потоках в региональном разрезе. Однако основной причиной отсутствия таких моделей является то, что исследование тенденций в денежно-кредитной сфере ограничивалось макроуровнем подобные блоки имелись только в народнохозяйственных моделях. [c.130]
Брок (Bro k), Хоммес (Hommes) и коллеги [54, 58, 55, 56, 57, 200, 257] разработали модели финансовых рынков, как систем "адаптивных верований" ограниченно рациональных агентов, использующих различные конкурирующие [c.138]
Заметим, что вопрос о справедливости сходимости (1) и для приведенных двух "классических" моделей, и для других моделей финансовых рынков - это, как следует из сказанного, только часть обшей проблемы сходимости (Вп,3п)-ръшковк "предельному" (.В, 5)-рьшку. Не менее важен также и вопрос о сходимости при п —> оо законов [c.232]
Кейнсианская модель финансового рынка носит несколько иной характер. Важное различие связано с трактовкой спроса на деньги. Согласно кейнсианской модели, кассовые остатки отдельных лиц можно разделить на две части. Во-первых, имеются трансакцишшые остатки, которые хранятся для осуществления сделок" связанных с поддержанием заданного уровня денежного дохода. Во-вторых, имеются спекулятишще остатки, которые хозяйственные субъекты хранят в качестве активов или инвестиций и которые не используются для осуществления сделок, за исключением покупки и продажи других финансовых активов, облигаций. Спрос на трансакцион-ные остатки зависит от уровня денежного дохода точно так же, как спрос на деньги в грубой количественной теории. Спрос же на спекулятивные остатки зависит от ставки процента по облигациям-чем выше норма процента, тем ниже спрос на спекулятивные остатки. Более детально эта теория спроса на деньги разъясняется в гл. 9, но мы уже сейчас имеем достаточно элементов, чтобы построить кейнсианскую модель денежного рынка. [c.281]
Смотреть страницы где упоминается термин Модель финансового рынка
: [c.319] [c.182] [c.156] [c.162] [c.186] [c.71]Смотреть главы в:
Финансовый рынок. Инструменты и методы прогнозирования -> Модель финансового рынка
