Результаты анализа должны включать оценки критического значения коэффициента корреляции гп для гипотезы / = 0 на определенном уровне значимости. Это позволяет не принимать во внимание статистически незначимые коэффициенты корреляции. Статистические пакеты позволяют получить значения корреляционной функции с указанием лагов и их графики. [c.103]
Расчет взаимодействия между результирующим параметром и независимым фактором с помощью корреляционных функций. Несмотря на очевидные достоинства корреляционного метода анализа, у него есть существенный недостаток — поведение и ре- [c.60]
Корреляционные функции позволяют более глубоко исследовать взаимозависимости различных переменных. Здесь приведены только самые общие понятия. При помощи этих функций можно исследовать различные классы зависи- мостей, в том числе и многомерные. Однако [c.62]
В качестве корреляционных функций используются показательные функции [c.125]
Анализ кросс-корреляционных функций показывает, что последующие изменения про- [c.116]
Таким образом, при условии, что автокорреляционная функция задана, уравнения (5.23) и (5.24) можно использовать для вычисления взаимной корреляционной функции R t ). [c.222]
Оценка вероятности истощения запаса ресурса. Для того чтобы выяснить, насколько грубой является полученная выше оценка (7.57), найдем вероятность истощения запаса ресурса A(t) в предположении, что ро(1) является гауссовым стационарным случайным процессом с корреляционной функцией вида [c.258]
Нетрудно показать, что для линейной зависимости (7.54) потока закупок от разности цен этот поток при р = р (PQ) также является гауссовым случайным процессом с корреляционной функцией [c.258]
Такой корреляционной функции соответствует спектральная плотность [c.258]
Выражения для корреляционных функций получено в [9.13] только для случайных процессов типа гибели размножения. [c.342]
В нелинейных моделях прогноза для вычисления моментов оценки прогноза недостаточно знания математического ожидания и корреляционной функции случайного процесса %(t). В общем случае требуется информация о дополнительных статистических характеристиках, а иногда и о системе функций распределения значений (0- [c.40]
Математические ожидания т = т), яу= и корреляционные функции k (t )> k (ti> Ъ) и k >(tiZ ts) случайных процессов i](t) и t(t) предполагаются известными или определяются на предварительном этапе решения задачи. Будем считать, что в каждый момент времени t случайные величины v (>t) и ,( ) имеют конечные математические ожидания и ограниченные дисперсии. [c.302]
Корреляционные функции k. и kw при условии (2.1) вычисляются по формулам [c.312]
Представление (4.5) позволяет легко переходить от анализа корреляционных функций случайных процессов и функций веса фильтров к исследованию спектральных плотностей случайных функций и амплитудно-частотных характеристик сглаживающих и прогнозирующих устройств. [c.313]
При некоторых дополнительных предположениях о характере процессов т) и и, следовательно, об их корреляционных функциях уравнения (4.4) и (4.6) могут быть решены. Полученные при этом функции веса определяют схему линейного фильтра или линейную вычислительную процедуру сглаживания и прогнозирования, оптимальную в смысле задачи (4.1). [c.313]
Анализ пространственно-временного сглаживания и экстраполяции и построение соответствующих фильтров существенно упрощается, если разделить решение задачи на два последовательных этапа — пространственное сглаживание и временную фильтрацию и упреждение. В двумерном случае пространственная фильтрация может быть реализована, например, на оптическом фильтре. Выбор функции веса для пространственной фильтрации не требует ограничений на физическую реализуемость, которая должна быть учтена при построении временных фильтров. Это упрощает расчет оптимальных пространственных фильтров. Задача еще больше упрощается в случае однородного поля, когда корреляционная, функция случайного поля зависит только от одного пространственного параметра. Следует, однако, иметь в виду, что разделение пространственно-временной фильтрации на два этапа представляет собой, вообще говоря, искусственную операцию и может снизить достижимое качество сглаживания и экстраполяции. [c.316]
Процесс (/) представляет собой белый шум, т. е. случайный процесс, корреляционная функция которого — дельта-функция Дирака. Напомним, что все предшествующие утверждения главы относились к случайным процессам с непрерывными корреляционными функциями. [c.322]
Определенная выражением (38) корреляционная функция обладает следующими свойствами. [c.184]
При т = 0 корреляционная функция р(0) = x(t) x(i) = Р = о максимальна и равна дисперсии стационарного случайного процесса (рис. 71.). Если измеряемой физической величиной является, например, сила тока г (г), то р(0) = г2 - полная мощность, выделяемая на сопротивлении в 1 Ом. В том случае. когда процесс имеет постоянную и переменную [c.184]
| Рис. 71. Корреляционная функция стационарного случайного процесса Максимальное значение корреляционной функции при т = 0 объясняется тем, что статистическая связь между неразличимыми по времени значениями x(t) является наибольшей. Корреляционную функцию часто нормируют по ее максимальному значению г (т) — р (т) /р (0), тогда г (0) = 1. | 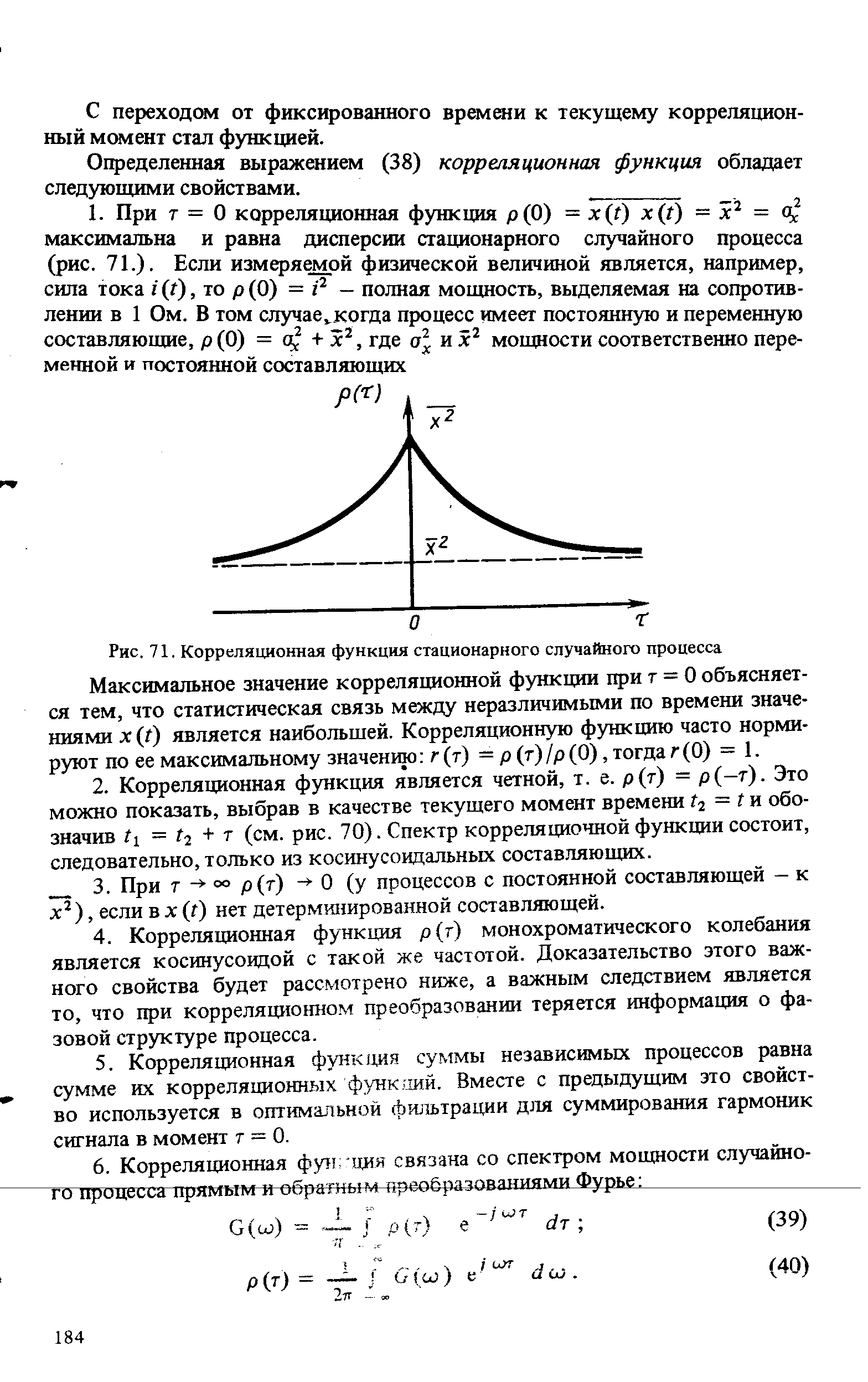 |
Корреляционная функция связана со спектром мощности случайно-то процесса прямым и обратным прообразе [c.184]
Корреляционная функция является основной характеристикой стационарных случайных процессов, поддающейся измерению и определяющей их внутренние статистические свойства. На практике, однако, из-за конечности времени усреднения Т определяется не сама корреляционная функция (38), а ее оценка [c.185]
Пример 46. Найдем корреляционную функцию гармонического колебания = Um sin (ijt+
[c.185]
Оценка корреляционной функции
[c.185]
Так как корреляционная функция р(т) = Шп р(т) = os WT, то поправка
[c.185]
Рис. 72. корреляционная функция гармонического процесса и поправка при
[c.185]
| Рис. 73. Измерение корреляционной функции в реальном масштабе времени | 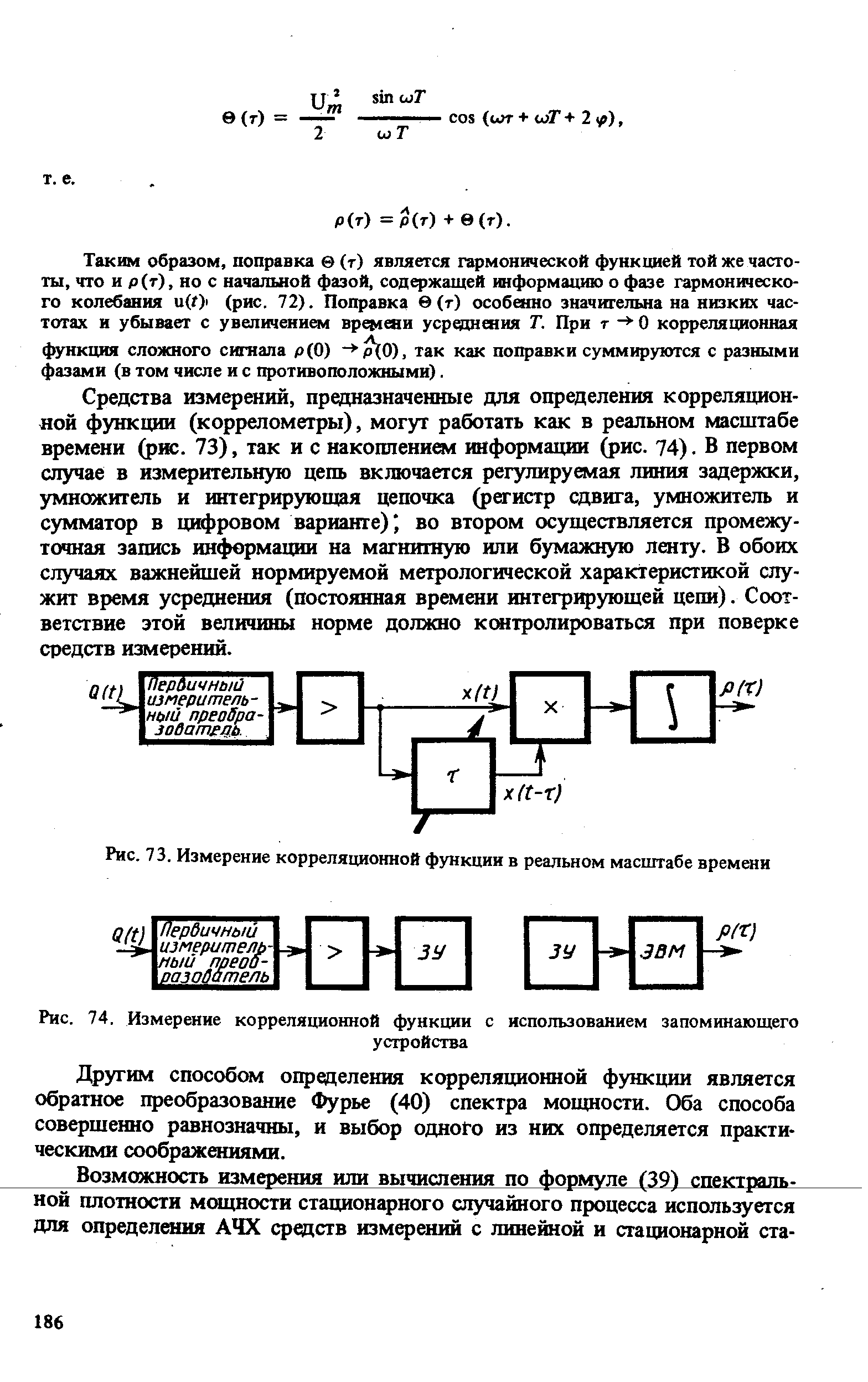 |
| Рис. 74. Измерение корреляционной функции с использованием запоминающего | 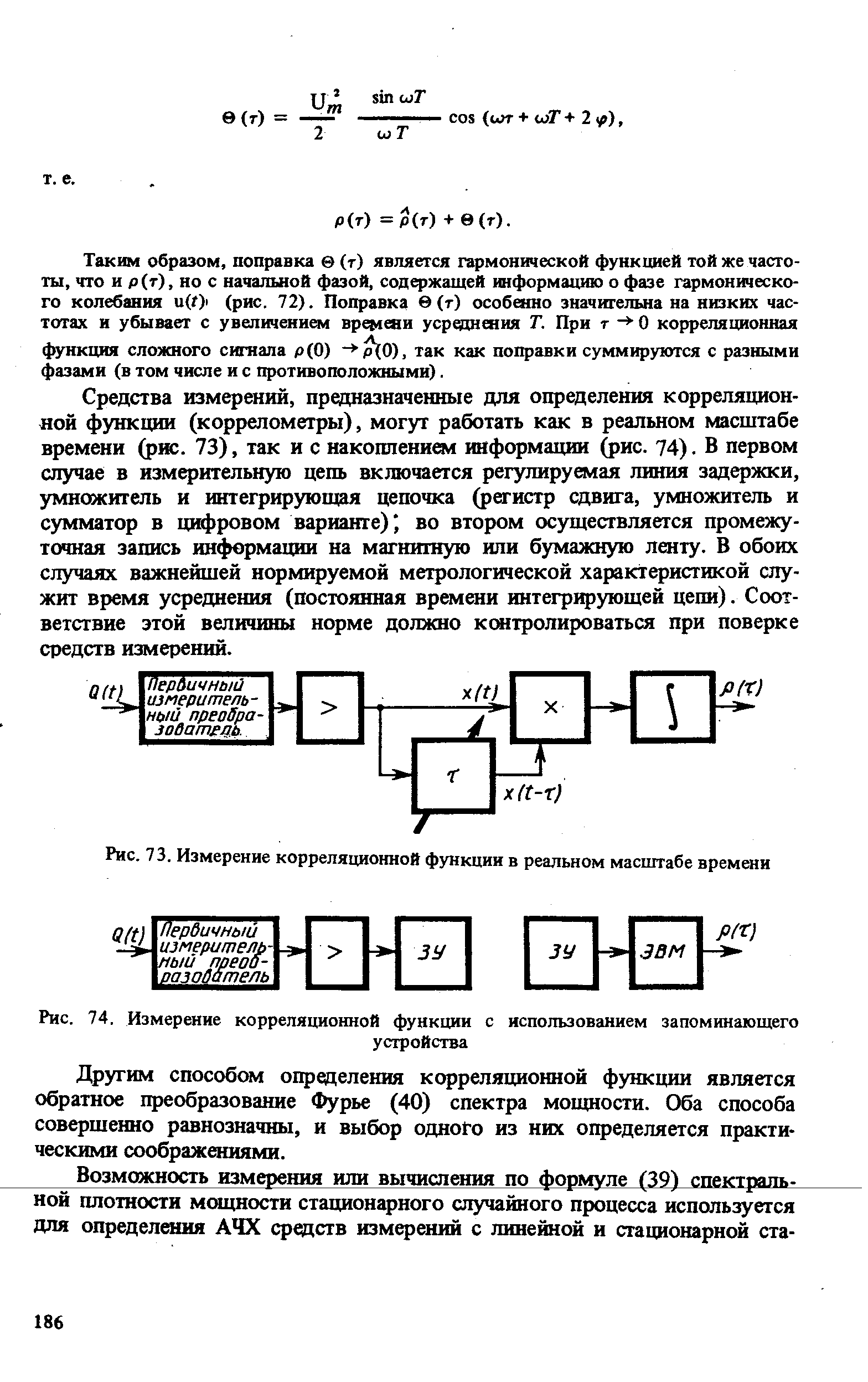 |
Пространственная корреляционная функция однородного и изотропного случайного поля [c.187]
Пространственно-временная корреляционная функция стационарного (по времени), однородного и изотропного (в пространстве) случайного поля [c.188]
БШ — блоки статистических моделей. В таких блоках могут объединяться расчеты по моделям вида Б3.1 и Б3.2. Например, в блоке прогнозирования урожайности могут объединяться трендовые модели прогноза отдельных факторов изменения урожайности с много-факторной моделью прогнозирования урожайности. Примером более сложного блока статистических моделей являются эконометрические модели народнохозяйственного, регионального или отраслевого уровня, в которых при помощи экстраполяционных полиномов, корреляционных функций и регрессионных зависимостей устанавливается статистическая взаимосвязь между совокупностью характеризующих данный объект планирования экзогенных и эндогенных показателей. К таким моделям относятся, в частности, модели, разработанные в Украинском филиале НИИПиНа (УКР-1 и УКР-2), в НИИЭПе Госплана Литовской ССР и др. [c.136]
Kp(t)->0 . Кр(т)=1 Кр(т)->б(г) г °2 k+l=N, где Kp(t)- корреляционная функция 8(т)- функция Хэвисайда (k+1) - число констант модели. [c.171]
График корреляционной функции для минутных приращений индекса S P500 на основе ценовой динамики этого индекса 20 июня 1995 года представлен на Рис. 13. Корреляционная функция с временным лагом т, есть не что иное, как статистическая мера силы связи, с которой текущие изменения цены связаны с аналогичными приращениями цены на временном интервале т в прошлом. Такая функция называется автокорреляционной функцией, так как характеризует "память" изучаемого процесса, то есть ту меру причинности (линейной) которая содержится во временном ряду. Говоря другими словами, эта функция определяет, может ли быть предсказано будущее исходя из информации, заключенной в прошлых значениях. Сумма всех корреляционных функций для всех возможных временных лагов (от 1 до бесконечности), прямо пропорциональна числу случаев, когда будущие приращения цен будут близки их текущим приращениям по причинам, отличным от чистой случайности. Корреляционная функция равная нулю для всех ненулевых временных лагов подразумевает тот факт, что приращения являются случайными, как в игре в кости. Корреляция равная 1 соответствует абсолютному совпадению, которое наблюдается только для ценовых приращений сравниваемых сами с собой. Необходимо заметить, что нулевая корреляционная функция, не полностью устраняет возможность предсказания цен в будущем, поскольку другие алгоритмы обнаружения взаимосвязи, в частности, использующие, по крайней мере, три приращения (соответствующие, так называемой, "нелинейной корреляции") возможно лучше улавливают ценовую динамику. [c.48]
Однако, такую зависимость значительно труднее определить, исследовать и далее использовать (см. главу №3). Как видно из Рис. 18 корреляционная функция является ненулевой только на очень ограниченном интервале времени, обычно на протяжении нескольких минут. Это означает, что на интервале более чем несколько минут будущие ценовые изменения не могут быть спрогнозированы простой (линейной) экстраполяцией прошлого1. [c.48]
| Рис. 18. Корреляционная функция приращений индекса S P500 на минутной шкале для одного дня 20 июня 1995 года, график которого представлен на Рис. 13. Отметим резкое изменение корреляции до нуля в течение нескольких минут с незначительными осцилляциями. Этот фафик подтверждает, что в изменении цены существует постоянная составляющая, длящаяся немногим более одной минуты. После двух минут тенденция цены становится реверсивной с ярко выраженной антикорреляцией (отрицательной корреляцией) соответствующей некоторому развороту цены. На более продолжительном интервале корреляция неотличима от шума. | 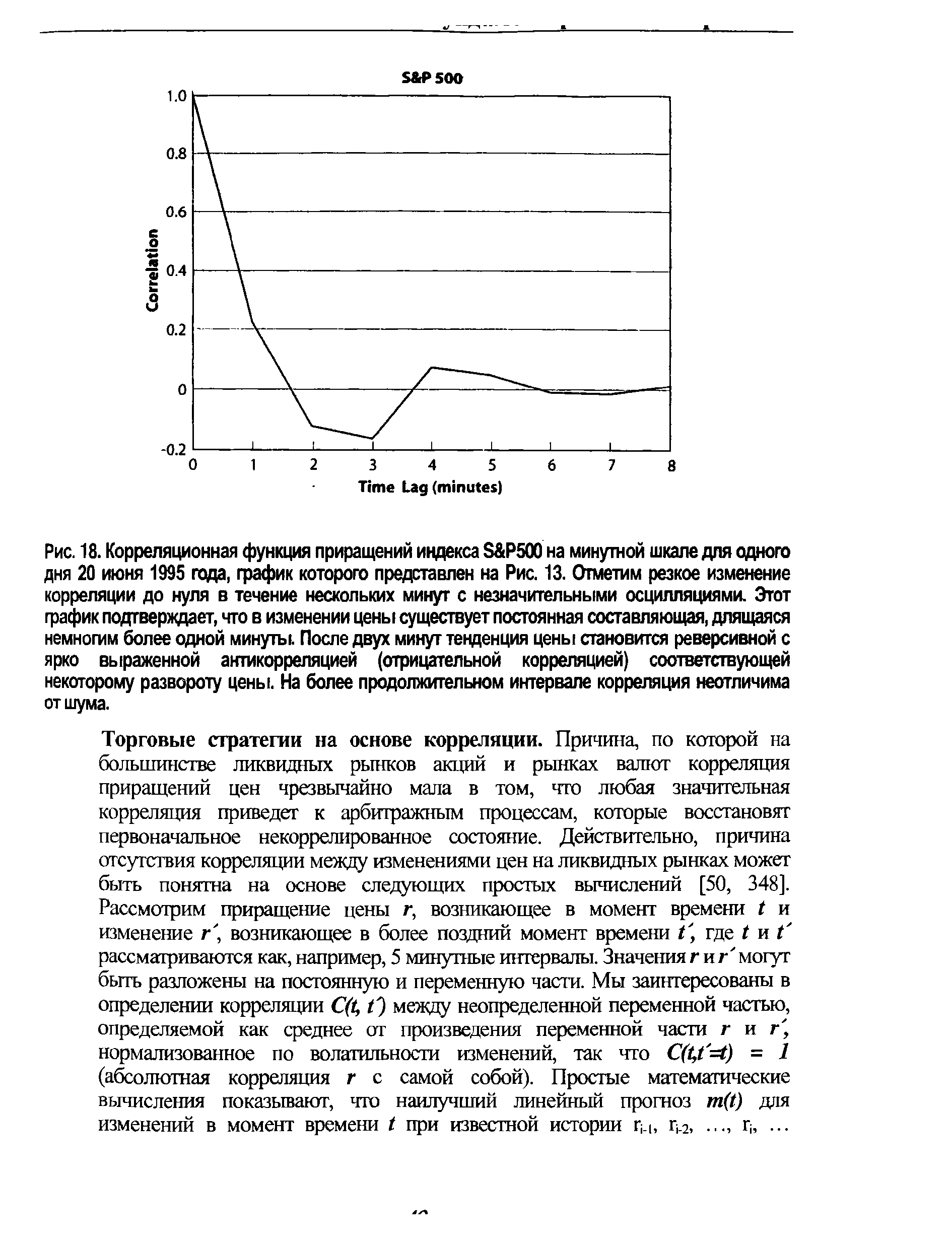 |
Рис. 81 иллюстрирует зависимость размерности фрактальной структуры троичного канторова множества как функцию уровня разрешения. Данная величина называется корреляцией и подсчитывает число пар точек в канторовом множестве, отделенных друг от друга расстоянием меньшим, чем разрешение. В таком двойном логарифмическом представлении наклон линии должен быть равен действительной фрактальной размерности d=ln2/ln3=0,6309..., поскольку корреляционная функция растет согласно разрешению, возведенному в степень d. Здесь мы снова видим логопериодические осцилляции, осложняющие линейный в среднем, тренд с положительным, в среднем, наклоном. Данные логопериодические структуры отражают дискретную масштабную инвариантность канторова множества. [c.208]
Это среднее получило название корреляционной функции, или коварнации. [c.155]
Эту систему дифференциальных уравнений, СППР, интегрируя каким либо численным методом (его может выбрать руководитель, если в этом есть необходимость, если нет - система по умолчанию выбирает его сама) получает все необходимые численности состояний элементов системы обслуживания, а, следовательно, и характеристики эффективности ее работы (см. например, раздел 8.3). Кроме того, по желанию руководителя СППР в ряде случаев может, выполняя соответствующие расчеты, исследовать устойчивость получаемых решений и динамику моментов (дисперсией и корреляционных функций) рассматриваемых процессов обслуживания. [c.429]
Как мы видели, в линейном случае формула (4.2) эквивалентна интегральному уравнению Винера — Хопфа (4.4) или (4.6). Уравнение Винера — Хопфа допускает конструктивное решение три стационарных случайных процессах т) ( ) и (i) с дробно-рациональными спектральными плотностями. Напомним, что спектральная плотность стационарного случайного процесса представляет собой преобразование Фурье его корреляционной. функции k(ti — 4). При таких предположениях о случайных процессах т]( ) и ( ) решение задачи (4.1) при бесконечном наблюдательном времени получено Н. Винером [69], а при конечном наблюдательном времени — Л. Заде и Л. Раггазини [121]. Другой подход к анализу этого случая предложен А. М. Ягломом [365]. [c.315]
Корреляционная функция является четной, т. е. р(т) = р(-т). Это можно показать, выбрав в качестве текущего момент времени 2 = f и обозначив = 2 + г (см. рис. 70). Спектр корреляционной функции состоит, следовательно, только из косинусоидальных составляющих. [c.184]
Корреляционная функция р(г) монохроматического колебания является косинусоидой с такой же частотой. Доказательство этого важного свойства будет рассмотрено ниже, а важным следствием является то, что при корреляционном преобразовании теряется информация о фазовой структуре процесса. [c.184]
Это положение известно как теорема преобразования Винера-Хинчина. Таким образом, спектр мощности, как и корреляционная функция, может служить неслучайной характеристикой случайного процесса. [c.185]
Пространственно-временной спектр мощности" стационарного, однородного и изотропного случайного поля связан с его пространственно-временной корреляционной функцией соотношениями Винера-Хинчина [c.188]
Смотреть страницы где упоминается термин Корреляционная функция
: [c.61] [c.119] [c.470] [c.174]Справочник по математике для экономистов (1987) -- [ c.299 ]
