Нормированной корреляционной функцией случайной функции X(t) называется функция [c.300]
Если аргументы функции — случайные независимые величины, т.е. между ними нет корреляционных связей, то характеристики функций вполне определяются математическим ожиданием и дисперсией ее аргументов. Далее в этой главе рассмотрены только функции независимых аргументов. [c.45]
В нелинейных моделях прогноза для вычисления моментов оценки прогноза недостаточно знания математического ожидания и корреляционной функции случайного процесса %(t). В общем случае требуется информация о дополнительных статистических характеристиках, а иногда и о системе функций распределения значений (0- [c.40]
Представление (4.5) позволяет легко переходить от анализа корреляционных функций случайных процессов и функций веса фильтров к исследованию спектральных плотностей случайных функций и амплитудно-частотных характеристик сглаживающих и прогнозирующих устройств. [c.313]
Анализ пространственно-временного сглаживания и экстраполяции и построение соответствующих фильтров существенно упрощается, если разделить решение задачи на два последовательных этапа — пространственное сглаживание и временную фильтрацию и упреждение. В двумерном случае пространственная фильтрация может быть реализована, например, на оптическом фильтре. Выбор функции веса для пространственной фильтрации не требует ограничений на физическую реализуемость, которая должна быть учтена при построении временных фильтров. Это упрощает расчет оптимальных пространственных фильтров. Задача еще больше упрощается в случае однородного поля, когда корреляционная, функция случайного поля зависит только от одного пространственного параметра. Следует, однако, иметь в виду, что разделение пространственно-временной фильтрации на два этапа представляет собой, вообще говоря, искусственную операцию и может снизить достижимое качество сглаживания и экстраполяции. [c.316]
Важнейшая характеристика случайной функции, определяющая тесноту связи между ее различными сечениями — корреляционная функция. [c.102]
Следовательно, в качестве основных характеристик случайной функции достаточно рассматривать ее математическое ожидание и корреляционную функцию. [c.102]
Связь между дифференциальными (разностными) уравнениями и корреляционными функциями случайных процессов [c.163]
В рамках корреляционной теории случайных процессов[26] и применительно к линейным дифференциальным (разностным) уравнениям, УСТАНОВЛЕНЫ СВЯЗИ между структурой, порядком и коэффициентами дифференциальных (разностных) уравнений, в правой части которых присутствует случайный процесс белого шума - с одной стороны, и структурой и параметрами КОРРЕЛЯЦИОННЫХ ФУНКЦИЙ решений указанных уравнений - с другой стороны. Например, дифференциальные уравнения 1- го и 2 - го порядка, описывают случайные процессы с корреляционными функциями следующих видов[25] [c.164]
Совершенно очевидно, что эти требования входят в противоречие со статистической природой процессов, протекающих на финансовом рынке. Если опираться на корреляционную теорию случайных процессов[26] и поставить при этом требование спрогнозировать поведение случайного процесса за периодом времени затухания его корреляционной функции, то совершенно очевидно, что это сделать невозможно. В данном случае ошибка прогнозирования будет равна дисперсии оцениваемого процесса, и само прогнозирование потеряет практический смысл. [c.201]
Модуль синтеза математической модели финансового рынка На основе известных соотношений[4,25] между корреляционными функциями случайных процессов и дифференциальными (разностными) уравнениями идентифицируются векторно-матричные дифференциальные (разностные) уравнения, описывающие статистическую динамику финансового рынка. [c.228]
При ti — tz корреляционная функция равна дисперсии случайной функции Kx(ti, t = Dx(t . [c.300]
При каноническом разложении случайной функции ее корреляционная функция выражается в виде [c.300]
Случайная функция X (t) называется стационарной в широком смысле, если ее математическое ожидание постоянно, а корреляционная функция зависит только от разности аргументов tt и t2 [c.300]
При использовании статистических методов в основном применялись два критерия аппроксимации случайных функций. Первый критерий состоит в выполнении условия равенства математических ожиданий и дисперсий и/или корреляционных моментов соответственно истинной и аппроксимирующей случайных функций. Второй критерий состоит в минимизации математического ожидания квадрата разности истинной и аппроксимирующей функции. С точки зрения простоты [c.96]
Определение 4. Пусть x(s) и y(t) случайные функции неслучайных аргументов seF, и /е 7, , x(s)eX(s) Z(tl y(t)eY(t) Z(t). Здесь Тх и Ту - область определения функций x(s) и y(t) соответственно. Тогда обобщенной (функциональной) взаимной корреляционной функцией двух случайных функций y(t] и x(s) называется обобщенная ковариация значений этих функций при произвольно взятых значениях их аргументов [c.102]
Определение 7. D-нормированной обобщенной взаимной корреляционной функцией r (t,s) случайных функций y(f) и j ( ) называется функция вида [c.103]
Из выражения (22) при у(/) = дг(/), Ту =ТХ следует выражение для D-нормированной обобщенной взаимной корреляционной функции случайного процесса (/). Из выражений (20), (21) и (22) видно, что в общем случае rfx(t,s) Ф r a(t,s), a [c.103]
Определение 9. Максимальной взаимной корреляционной функцией случайных процессов y(t) и x(s) R t s) [15] называется обобщенная взаимная корреляционная функция, в которой операторы В ч С определены из условия [c.103]
Корреляционная зависимость между случайными величинами X и 7 называется линейной корреляцией, если обе функции регрессии Хна 7 и 7 на X являются линейными. [c.93]
Оценка вероятности истощения запаса ресурса. Для того чтобы выяснить, насколько грубой является полученная выше оценка (7.57), найдем вероятность истощения запаса ресурса A(t) в предположении, что ро(1) является гауссовым стационарным случайным процессом с корреляционной функцией вида [c.258]
Нетрудно показать, что для линейной зависимости (7.54) потока закупок от разности цен этот поток при р = р (PQ) также является гауссовым случайным процессом с корреляционной функцией [c.258]
Кроме вышесказанного для расчета специфицированной нормы производственного запаса необходимо в рассматриваемом случае дополнительно использовать плотность распределения случайной двухмерной величины нормируемой марки материального ресурса у предприятия-потребителя. Ее следует рассчитать по данным отчетного года — QU (плотности условных распределений объемов поставок Q = qi при постоянных значениях суммарных объемов суточных отпусков за интервал поставки U = ит, где т сохраняет одно и то же значение при всех возможных значениях Q)1. Здесь суммарный объем суточных отпусков за интервал поставки является факторным признаком, а объем поставки (зависимый признак) — результативным. Между факторным и результативным признаками проявляется корреляционная связь. При такой связи на величину результативного признака оказывают влияние, помимо факторного, множество других признаков, действующих в различных направлениях одновременно или последовательно. При этом сами вариации суточных объемов отпусков и интервалов поставок можно рассматривать как случайные независимые события, а их значения — как случайные независимые величины. В то время как их произведение (суммарный объем отпуска за интервал поставки) в рассматриваемом случае коррелирует с объемом поставки. Доказательством того, что вышеуказанные факторы (объемы суточных отпусков и интервалы поставки) случайные независимые величины, является количественное несоответствие значений факторов — много значений суточных объемов отпуска и значительно меньше интервалов поставок. Часто корреляционную связь называют неполной статистической или частичной в отличие от функциональной связи, которая выражается в том, что при определенном значении одной переменной величины (независимая переменная — аргумент) другая переменная величина (зависимая переменная — функция) принимает строго определенное значение. Корреляционную связь можно выявить только в виде общей тенденции при массовом сопоставлении фактов. При этом каждому значению факторного признака будет соответствовать не одно определенное значение результативного признака, а их совокупность. В этом выражается имеющаяся свободная связь между объемом поставки и суммарным объемом суточных отпусков в нем. Плотность распределения случайной двухмерной величины (Qf/), отражающая количественно имеющуюся связь между факторными признаками, выглядит следующим образом [c.363]
Выражения для корреляционных функций получено в [9.13] только для случайных процессов типа гибели размножения. [c.342]
Математические ожидания т = т), яу= и корреляционные функции k (t )> k (ti> Ъ) и k >(tiZ ts) случайных процессов i](t) и t(t) предполагаются известными или определяются на предварительном этапе решения задачи. Будем считать, что в каждый момент времени t случайные величины v (>t) и ,( ) имеют конечные математические ожидания и ограниченные дисперсии. [c.302]
Процесс (/) представляет собой белый шум, т. е. случайный процесс, корреляционная функция которого — дельта-функция Дирака. Напомним, что все предшествующие утверждения главы относились к случайным процессам с непрерывными корреляционными функциями. [c.322]
Элементы корреляционной матрицы, k определяются случайными величинами С" или в линейном случае [в силу"7 (2.3)] функциями [веса Р ( 0, т). Поэтому критерий качества прогноза Р( ар . ) можно рассматривать как некоторый функционал от С" или функционал от Р- (ta, т) v [c.324]
При т = 0 корреляционная функция р(0) = x(t) x(i) = Р = о максимальна и равна дисперсии стационарного случайного процесса (рис. 71.). Если измеряемой физической величиной является, например, сила тока г (г), то р(0) = г2 - полная мощность, выделяемая на сопротивлении в 1 Ом. В том случае. когда процесс имеет постоянную и переменную [c.184]
| Рис. 71. Корреляционная функция стационарного случайного процесса Максимальное значение корреляционной функции при т = 0 объясняется тем, что статистическая связь между неразличимыми по времени значениями x(t) является наибольшей. Корреляционную функцию часто нормируют по ее максимальному значению г (т) — р (т) /р (0), тогда г (0) = 1. | 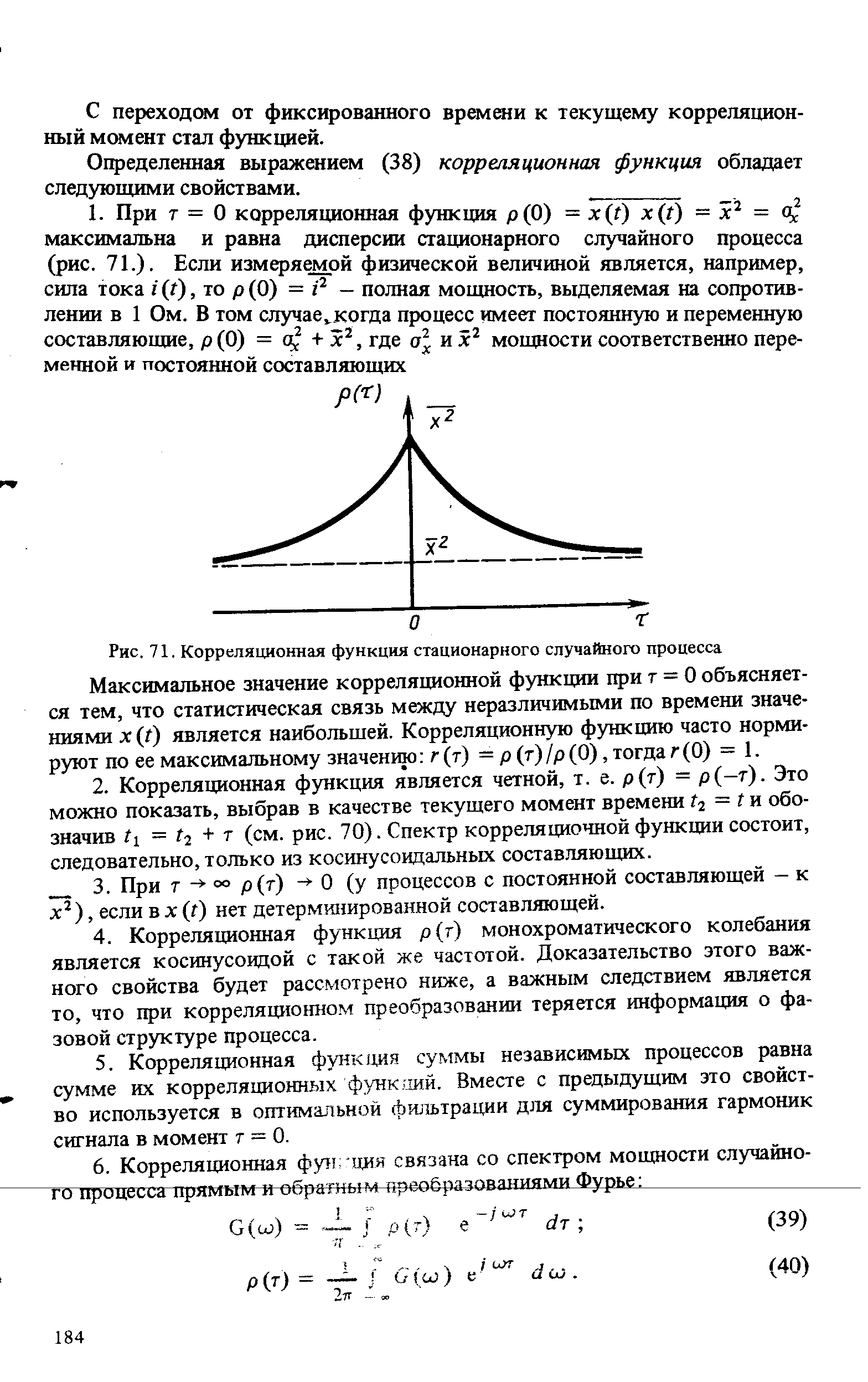 |
Корреляционная функция является основной характеристикой стационарных случайных процессов, поддающейся измерению и определяющей их внутренние статистические свойства. На практике, однако, из-за конечности времени усреднения Т определяется не сама корреляционная функция (38), а ее оценка [c.185]
Корреляционной функцией случайной функции X(t) называется такая неслучайшая функция Кх( , t2), которая для каждой пары сечеяий аргумента (tt, t2) равна соответствующему корреляционному моменту связи. [c.299]
Корреляционная теория случайных процессов[26] позволяет описывать статистические свойства процессов с помощью момент-ных характеристик, главными из которых (применительно к скалярным случайным процессам) являются начальный момент 1-го порядка - математическое ожидание, центральный момент 2-го порядка - дисперсия, автоковариационная функция случайного процесса и взаимно-ковариационная функция между различными скалярными процессами. В случае гауссовского закона распределения случайного процесса указанные моментные характеристики полностью определяют его вероятностные свойства. Важность корреляционной теории состоит также в том, что все случайные процессы с той или иной степенью точности могут быть аппроксимированы через гауссовские процессы[4,14] и, следовательно, выводы корреляционной теории будут справедливы для люб,ых случайных процессов. [c.167]
Если мы хотим в рамках корреляционной теории случайных процессов[26] далее оценивать эффективность торговли на рынке FOREX (на интервале времени t(l)...t(n)), мы должны оценить моментные характеристики эффективности торговли. К указанным моментным характеристикам в данном конкретном случае (см. рис. 10.7) будут относиться математическое ожидание ширины полосы между максимальной ценой лота валюты (верхняя линия) и минимальной ценой лота валюты (нижняя линия), то есть выигрыш спекулянта, а также корреляционная функция выигрыша (прибыли). Функция математического ожидания выигрыша (прибыли) - это некоторое среднее значение прибыли в функции времени. Корреляционная функция прибыли будет определять статистическую взаимосвязь между возможными мгновенными значениями прибыли в функции времени, а также степень разброса мгновенных значений прибыли относительно математического ожидания. [c.254]
Однако и этот случай вполне может быть описан достаточно корректной математической моделью в рамках корреляционной теории случайных процессов, при этом решение задачи может быть получено аналитическими методами. В частности, для решения указанной задачи необходимо предварительно иметь статистический портрет случайных процессов MAX(t), MIN(t), axft), Amm(t) в виде оценок их функций математических ожиданий и ковариационных функций, а также оценок вероятностей наступления событий в соответствии с классификацией, представленной на рис.10.8. [c.257]
Такого рода характеристика явлений, влияющих на уровень и динамику валютного курса, является непременным этапом, предшествующим самостоятельному статистическому анализу факторов на основе конкретного цифрового материала. Дальнейший анализ выглядит чаще как моделирование взаимосвязей и оценка тесноты взаимозависимости (корреляционно-регрессионный анализ). Напомним, что выбор функции осуществляется исходя из показателей значимости уравнения и ошибок аппроксимации. Это относительная ошибка аппроксимации, средняя квадратическая ошибка аппроксимации (6ОСТ) (чем они меньше, тем лучше уравнение) и коэффициент множественной детерминации (R2) или коэффициент множественной корреляции (R) (чем ближе он к 1, тем более вероятность, что уравнение регрессии носит совершенно случайный характер). Для проверки значимости используют F-критерий с распределением Фишера. [c.670]
График корреляционной функции для минутных приращений индекса S P500 на основе ценовой динамики этого индекса 20 июня 1995 года представлен на Рис. 13. Корреляционная функция с временным лагом т, есть не что иное, как статистическая мера силы связи, с которой текущие изменения цены связаны с аналогичными приращениями цены на временном интервале т в прошлом. Такая функция называется автокорреляционной функцией, так как характеризует "память" изучаемого процесса, то есть ту меру причинности (линейной) которая содержится во временном ряду. Говоря другими словами, эта функция определяет, может ли быть предсказано будущее исходя из информации, заключенной в прошлых значениях. Сумма всех корреляционных функций для всех возможных временных лагов (от 1 до бесконечности), прямо пропорциональна числу случаев, когда будущие приращения цен будут близки их текущим приращениям по причинам, отличным от чистой случайности. Корреляционная функция равная нулю для всех ненулевых временных лагов подразумевает тот факт, что приращения являются случайными, как в игре в кости. Корреляция равная 1 соответствует абсолютному совпадению, которое наблюдается только для ценовых приращений сравниваемых сами с собой. Необходимо заметить, что нулевая корреляционная функция, не полностью устраняет возможность предсказания цен в будущем, поскольку другие алгоритмы обнаружения взаимосвязи, в частности, использующие, по крайней мере, три приращения (соответствующие, так называемой, "нелинейной корреляции") возможно лучше улавливают ценовую динамику. [c.48]
АВТОКОРРЕЛЯЦИЯ [auto orrelation, serial orrelation] — корреляционная связь (см. Корреляция) между значениями одного и того же случайного процесса X ( ) в моменты времени tx и t. Функция, характеризующая эту связь, называется автокорреляционной функцией. [c.7]
МЕТОД НАИМЕНЬШИХ КВАДРАТОВ [least-square te hnique] — математический (математико-статистический) прием, служащий для выравнивания динамических рядов, выявления формы корреляционной связи между случайными величинами и др. Состоит в том, что функция, описывающая данное явление, аппроксимируется более простой функцией. Причем последняя подбирается с таким расчетом, чтобы среднеквадратичное отклонение (см. Дисперсия) фактических уровней функции в наблюдаемых точках от выровненных было наименьшим. [c.196]
Как мы видели, в линейном случае формула (4.2) эквивалентна интегральному уравнению Винера — Хопфа (4.4) или (4.6). Уравнение Винера — Хопфа допускает конструктивное решение три стационарных случайных процессах т) ( ) и (i) с дробно-рациональными спектральными плотностями. Напомним, что спектральная плотность стационарного случайного процесса представляет собой преобразование Фурье его корреляционной. функции k(ti — 4). При таких предположениях о случайных процессах т]( ) и ( ) решение задачи (4.1) при бесконечном наблюдательном времени получено Н. Винером [69], а при конечном наблюдательном времени — Л. Заде и Л. Раггазини [121]. Другой подход к анализу этого случая предложен А. М. Ягломом [365]. [c.315]
Это положение известно как теорема преобразования Винера-Хинчина. Таким образом, спектр мощности, как и корреляционная функция, может служить неслучайной характеристикой случайного процесса. [c.185]
Смотреть страницы где упоминается термин Корреляционная функция случайной функции
: [c.104] [c.131] [c.104] [c.105] [c.105] [c.162] [c.162]Смотреть главы в:
Справочник по математике для экономистов -> Корреляционная функция случайной функции
