Корреляционный анализ состоит в установлении корреляционных связей между отдельными факторами исследуемого процесса, причем корреляционная связь выявляет характер изменения одной величины при изменении другой. С этой целью при помощи методов множественной корреляции выводят уравнение, дающее зависимость планируемой величины от каждого из рассматриваемых факторов. Коэффициенты и степени при величинах показателей характеризуют влияние последних на планируемую величину. При анализе такого уравнения полезно выявить факторы, влияние которых незначительно, и исключить их из рассмотрения. [c.152]
Функциональную зависимость можно установить методом множественной корреляции по факторам, влияющим на величину удельных затрат с установлением тесноты корреляционной связи раздельно для каждого из учитываемых в расчете факто-риальных признаков при одновременном их действии. Многофакторный корреляционный анализ как статистический метод является наиболее целесообразным средством выявления влияния многих факторов на уровень себестоимости нефти. [c.155]
В экономических расчетах может быть также использован прием корреляционной связи, являющийся одним из методов математической статистики. Этот метод позволяет определять зависимость различной степени связи между рассматриваемыми факторами в условиях, когда связь не является пропорциональной. В этом случае математически определяется форма и теснота связи, т. е. степень ее влияния на исследуемый показатель. Например, с помощью корреляционной связи может быть установлена степень изменения уровня производительности труда при внедрении новой техники. Широкие возможности ЭВМ позволяют ставить вопрос о необходимости их применения для проведения экономических расчетов, моделирующих производственно-хозяйственную деятельность таких сложных систем, как закольцованные газопроводы. Проводимые научные исследования показали, что для целей анализа влияния различных факторов (диаметр газопровода, энергоемкость, грузонапряженность и т. д.) могут быть широко использованы вероятностные методы корреляции. [c.80]
Следующий этап исследования — определение тесноты связи между факторами и исследуемым показателем, а также между самими факторами с применением методов корреляционного анализа. На этом этапе вычисляют парные и частные коэффициенты корреляции и другие показатели, характеризующие тесноту корреляционной связи между переменными. [c.28]
Аналогично, все значимые требования клиента на основании корреляционной связи с показателями (свойствами) изделия переводятся в технические спецификации. [c.51]
Разработка экономико-математических моделей прогнозирования бюджетов также базируется на данных консолидированных бюджетов. Для расчета финансовых ресурсов на перспективу исследуются корреляционные связи между объемами доходов консолидированных бюджетов и такими переменными, как размер ВВП, национального дохода, объемом валовой продукции промышленности, сельского хозяйства. [c.109]
Для расчетов основных показателей федерального бюджета на перспективу могут быть использованы корреляционные связи между объемом доходов федерального бюджета и двумя переменными произведенным национальным доходом и валовой продукцией промышленности и сельского хозяйства, а также связь между этими показателями и налогом на прибыль. Коэффициенты корреляции показывают большую тесноту в изучаемых связях, поскольку доходы бюджета формируются прежде всего за счет национального дохода, а связь между налогом на прибыль и самой прибылью очевидна. [c.152]
Стохастический анализ представляет собой методику исследования факторов, связь которых с результативным показателем в отличие от функциональной является неполной, вероятностной (корреляционной). Если при функциональной (полной) зависимости с изменением аргумента всегда происходит соответствующее изменение функции, то при корреляционной связи изменение аргумента может дать несколько значений прироста функции в зависимости от сочетания других факторов, определяющих данный показатель. К примеру, производительность труда при одном и том же уровне фондовооруженности может быть неодинаковой на разных предприятиях. Это зависит от оптимальности сочетания других факторов, воздействующих на этот показатель. [c.28]
Основу экономических исследований должен составлять глубокий качественный анализ. Наряду с этим для обоснования текущих п перспективных планов необходима количественная оценка процесса. Определение количественных взаимосвязей между уровнем себестоимости добычи нефти и попутного газа и факторами, влияющими на ее динамику, требует использования приемов и методов математической статистики. Одним из таких методов является корреляционно-регрессионный анализ. Отличительной особенностью корреляционных связей является их приближенный характер, поскольку каждое из рассматриваемых явлений находится под влиянием многочисленных причин. В связи с этим найти точную корреляционную связь можно лишь при изучении многих явлений. [c.58]
Поскольку прогнозирование носит вероятностный характер, оно в основном осуществляется с помощью статистических моделей. Они основываются, главным образом, на корреляционной связи между объектами изучения. Статистика помогает предвидеть, но сама по себе еще не обеспечивает правильность предвидения. Статистическими методами можно добиться высоких результатов, однако в конечном счете их надежность зависит от правильности выбора отправных положений. [c.101]
С помощью координатной сетки строятся графики зависимости, например, уровня издержек от объема произведенной и реализованной продукции, а также графики, на которых можно изображать и корреляционные связи между показателями. В системе осей координат изображение показывает влияние различных факторов на тот или иной показатель. [c.152]
Изучение взаимосвязи товарооборота и производительности труда может проводиться с применением статистико-мате-матических методов. Между товарооборотом и производительностью труда существует корреляционная связь, объем розничного товарооборота зависит не только от уровня производительности труда торговых работников, но и от других факторов. [c.305]
Поскольку корреляционная связь с достаточной выразительностью и полнотой проявляется только в массе наблюдений, объем выборки данных должен быть достаточно большим, так как только в массе наблюдений сглаживается влияние других факторов. Чем большая совокупность объектов исследуется, тем точнее результаты анализа. [c.140]
Если аргументы функции — случайные независимые величины, т.е. между ними нет корреляционных связей, то характеристики функций вполне определяются математическим ожиданием и дисперсией ее аргументов. Далее в этой главе рассмотрены только функции независимых аргументов. [c.45]
Метод оценки корреляционной связи и тип определяемого при этом коэффициента зависит от закона распределения данных. [c.86]
Так, средними в широком смысле слова являются такие показатели, как доля мужчин в общем числе жителей страны (ведь эта доля разная в разных регионах), плотность населения, коэффициент смертности, ожидаемая продолжительность жизни родившихся в данном году и др. Рассматриваемые далее в этой главе показатели вариации признака в совокупности, а также в главе 8 показатели корреляционной связи тоже средние в широком смысле слова, так как измеряют среднее различие между значениями одного признака у разных единиц совокупности или среднюю связь вариации одного признака с вариацией другого. [c.91]
ПОНЯТИЕ О СТАТИСТИЧЕСКОЙ И КОРРЕЛЯЦИОННОЙ СВЯЗИ [c.226]
Корреляционной связью называют важнейший частный случай статистической связи, состоящий в том, что разным значениям одной переменной соответствуют различные средние значения другой. С изменением значения признака х закономерным образом изменяется среднее значение признака у в то время как в каждом отдельном случае значение признака у (с различными вероятностями) может принимать множество различных значений. [c.228]
Статистическая связь между двумя признаками (переменными величинами) предполагает, что каждый из них имеет случайную вариацию индивидуальных значений относительно средней величины. Если же такую вариацию имеет лишь один из признаков, а значения другого являются жестко детерминированными, то говорят лишь о регрессии, но не о статистической (тем более корреляционной) связи. Например, при анализе динамических рядов можно измерять регрессию уровней ряда урожайности (имеющих случайную колеблемость) на номера лет. Но нельзя говорить о корреляции между ними и применять показатели корреляции с соответствующей им интерпретацией (см. гл. 9). [c.228]
Корреляционная связь между признаками может возникать разными путями. Важнейший путь - причинная зависимость результативного признака (его вариации) от вариации факторного признака. Например, признак х - балл оценки плодородия почв, признак у -урожайность сельскохозяйственной культуры. Здесь совершенно ясно логически, какой признак выступает как независимая переменная (фактор) х, какой - как зависимая переменная (результат) у. [c.229]
Совершенно иная интерпретация необходима при изучении корреляционной связи между двумя следствиями общей причины. Известен классический пример, приведенный крупнейшим статистиком России начала XX в. А. А. Чупровым если в качестве признака х взять число пожарных команд в городе, а за признаку - сумму убытков за год в городе от пожаров, то между признаками х и у в совокупности городов России существенна прямая корреляция в среднем, чем больше пожарников в городе, тем больше и убытков от пожаров Уж не занимались ли пожарники поджигательством из боязни потерять работу Но дело в другом. Данную корреляцию нельзя интерпретировать как связь причины и следствия оба признака - следствия общей причины - размера города. Вполне логично, что в крупных городах больше пожарных частей, но больше и пожаров, и убытков от них за год, чем в мелких городах. [c.229]
Поскольку корреляционная связь является статистической, первым условием возможности ее изучения является общее условие всякого статистического исследования наличие данных по достаточно большой совокупности явлений. По отдельным явлениям можно получить совершенно превратное представление о связи признаков, ибо в каждом отдельном явлении значения признаков кроме закономерной составляющей имеют случайное отклонение (вариацию). Например, сравнивая два хозяйства, одно из которых имеет лучшее качество почв, по уровню урожайности, можно обнаружить, что урожайность выше в хозяйстве с худшими почвами. Ведь урожайность зависит от сотен факторов и при том же самом качестве почв может быть и выше, и ниже. Но если сравнивать большое число хозяйств с лучшими почвами и большое число - с худшими, то средняя урожайность в первой группе окажется выше и станет возможным измерить достаточно точно параметры корреляционной связи. [c.230]
Вторым условием закономерного проявления корреляционной связи служит условие, обеспечивающее надежное выражение закономерности в средней величине. Кроме уже указанного большого числа единиц совокупности для этого необходима достаточная качественная однородность совокупности. Нарушение этого условия мо- [c.230]
В соответствии с сущностью корреляционной связи ее изучение имеет две цели [c.232]
При расчете г не по группировке, а по уравнению корреляционной связи (уравнению регрессии) мы используем формулу (8.3). В этом случае правило разложения суммы квадратов отклонений результативного признака записывается как [c.234]
Уравнение корреляционной связи измеряет зависимость между вариацией результативного признака и вариацией факторного признака (признаков). Меры тесноты связи измеряют долю вариации результативного признака, которая связана корреляционно с вариацией факторного признака (признаков). [c.235]
Простейшей системой корреляционной связи является линейная связь между двумя признаками - парная линейная корреляция. [c.238]
Уравнение парной линейной корреляционной связи называется уравнением парной регрессии и имеет вид [c.238]
Применение одной из формул (8.7), (8.8) или (8.9) зависит от характера данных и наличия уже вычисленных на предыдущих этапах анализа показателей. Если были вычислены х, у, ах, ст, то проще применить формулу (8.7) или (8.8). Если расчет параметров уравнения корреляционной связи ведется исходя из первичных данных х у,, то удобнее формула (8.9). Особенно существенно она сокращает объем вычислений при слабой вариации признаков, ибо тогда отклонения их индивидуальных значений от средних величин [c.240]
Теснота парной линейной корреляционной связи, как и любой другой показатель, может быть измерена корреляционным отношением ц. Кроме того, при линейной форме уравнения применяется другой показатель тесноты связи - коэффициент корреляции г . Этот показатель представляет собой стандартизованный коэффициент регрессии, т. е. коэффициент, выраженный не в абсолютных единицах измерения признаков, а в долях среднего квадратического отклонения результативного признака [c.241]
Графическое изображение корреляционной связи по данным табл. 8.1. приведено на рис. 8.1, [c.245]
Наиболее рациональным приемом анализа и расчета параметров корреляционной связи с помощью группировки является построение так называемой корреляционной решетки (табл. 8.3). Это таблица, в которой изучаемая совокупность сгруппирована одновременно по обоим признакам, связь между которыми изучается (двумерное распределение). Число групп по признакам может быть как равным, так и неравным. Если наибольшие числа частот каждой строки и каждого столбца располагаются на первой диагонали (в табл. 8.3 эти цифры подчеркнуты), связь является прямой и близкой к линейной если наибольшие числа частот располагаются вдоль второй диагонали (в табл. 8.3 эти цифры также подчеркнуты), связь обратная, линейная. Если частоты во всех клетках таблицы примерно равны, связи нет если наибольшие числа расположены по дуге, связь криволинейная. В табл. 8.3 кроме частот приведены строки и графы [c.255]
В качестве примера параболической корреляционной связи рассмотрим зависимость себестоимости молока от продуктивности коров по данным аналитической группировки сельхозпредприятий области (табл. 8.5). В этой же таблице приведены расчетные величины, входящие в уравнения МНК для параболы. [c.264]
| Таблица 8.5 Параболическая корреляционная связь продуктивности коров и себестоимости молока | 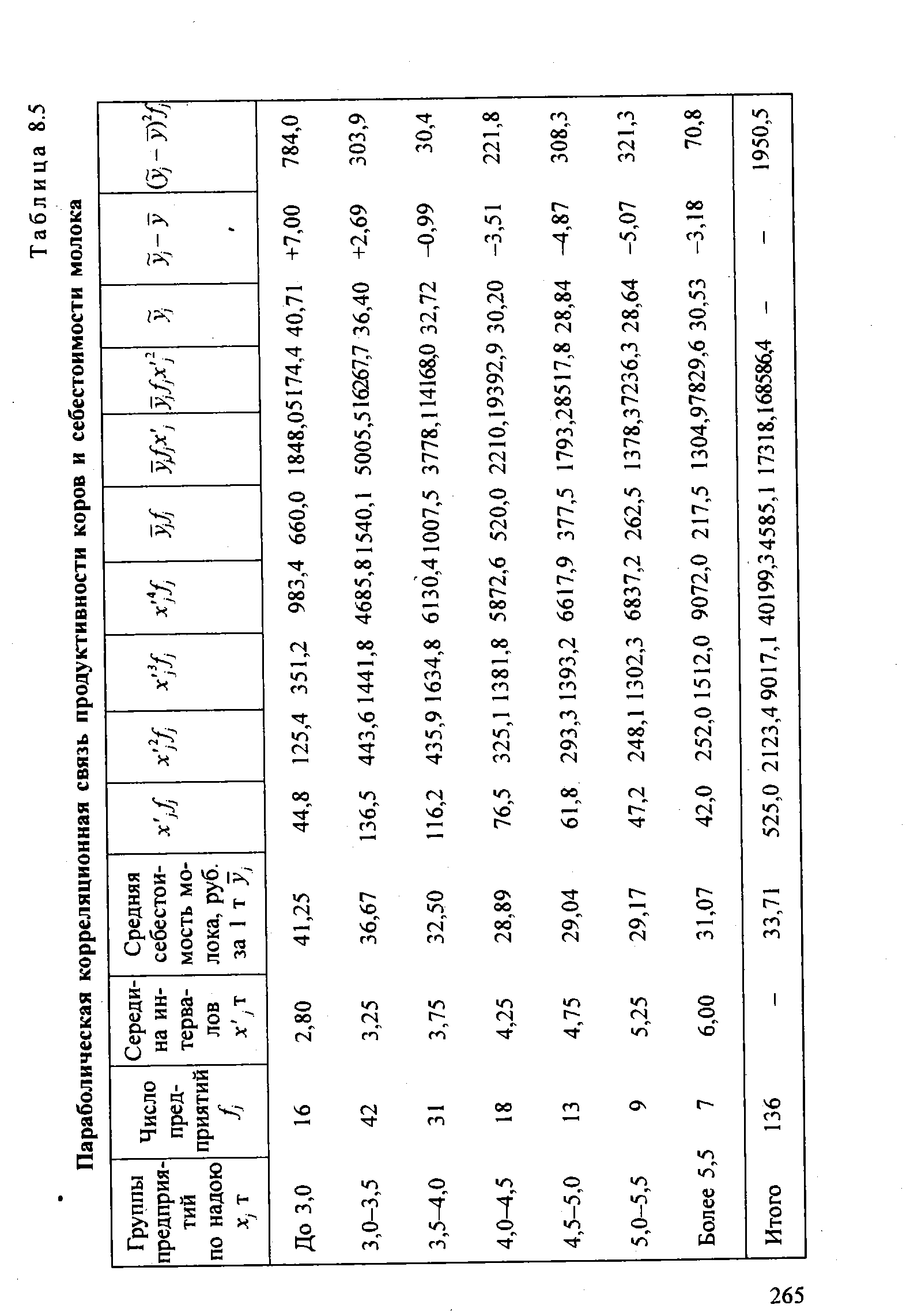 |
Напомним еще раз, что для получения надежных и достаточно точных показателей корреляционной связи необходима более многочисленная совокупность. [c.271]
| Таблица 8.12 Показатели множественной корреляционной связи |  |
При корреляции стоимостных оценок денежного потока и ставки дисконтирования, которая охарактеризуется коэффициентами корреляции, формулы 12.7,12.8, 12.10—12.14 не применяются. С учетом этой корреляционной связи йота-коэффициент текущей стоимости денежного потока в / -м году определяется выражением [c.137]
Следующий общий вопрос - это уже рассмотренный в разделе о группировке вопрос о чистоте измерения влияния каждого отдельного факторного признака. Как отмечалось в главе 6, группировка совокупности по одному факторному признаку может отразить влияние именно данного фактора на результативный признак при условии, что все другие факторы не связаны с изучаемым, а случайные отклонения и ошибки взаимопогасились в большой совокупности. Если же изучаемый фактор связан с другими факторами, влияющими на результативный признак, будет получена не чистая характеристика влияния только одного фактора, а сложный комплекс, состоящий как из непосредственного влияния фактора, так и из его косвенных влияний, через его связь с другими факторами и их влияние на результативный признак. Данное положение полностью относится и к парной корреляционной связи. [c.235]
Показатели корреляционной связи, вычисленные по ограниченной совокупности (по выборке), являются лишь оценками той или иной статистической закономерности, поскольку в любом параметре сохраняется элемент не полностью погасившейся случайности, присущей индивидуальным значениям признаков. Поэтому необходима статистическая оценка степени точности и надежности параметров корреляции. Под надежностью здесь понимается вероятность того, что значение проверяемого параметра не равно нулю, не включает в себя величины противоположных знаков. [c.247]
В том случае, если между изучемыми признаками нельзя установить очевидной подобной зависимости, т.е. причинность имеет скрытый характер, как это показано на рис. 3.2, , говорят о корреляционной связи признаков. В качестве примера подобной связи можно привести зависимость [c.74]
