Совершенно иная интерпретация необходима при изучении корреляционной связи между двумя следствиями общей причины. Известен классический пример, приведенный крупнейшим статистиком России начала XX в. А. А. Чупровым если в качестве признака х взять число пожарных команд в городе, а за признаку - сумму убытков за год в городе от пожаров, то между признаками х и у в совокупности городов России существенна прямая корреляция в среднем, чем больше пожарников в городе, тем больше и убытков от пожаров Уж не занимались ли пожарники поджигательством из боязни потерять работу Но дело в другом. Данную корреляцию нельзя интерпретировать как связь причины и следствия оба признака - следствия общей причины - размера города. Вполне логично, что в крупных городах больше пожарных частей, но больше и пожаров, и убытков от них за год, чем в мелких городах. [c.229]
Наиболее рациональным приемом анализа и расчета параметров корреляционной связи с помощью группировки является построение так называемой корреляционной решетки (табл. 8.3). Это таблица, в которой изучаемая совокупность сгруппирована одновременно по обоим признакам, связь между которыми изучается (двумерное распределение). Число групп по признакам может быть как равным, так и неравным. Если наибольшие числа частот каждой строки и каждого столбца располагаются на первой диагонали (в табл. 8.3 эти цифры подчеркнуты), связь является прямой и близкой к линейной если наибольшие числа частот располагаются вдоль второй диагонали (в табл. 8.3 эти цифры также подчеркнуты), связь обратная, линейная. Если частоты во всех клетках таблицы примерно равны, связи нет если наибольшие числа расположены по дуге, связь криволинейная. В табл. 8.3 кроме частот приведены строки и графы [c.255]
Если г > О Ь > 0), то корреляционная связь между переменными называется прямой, если г < О (Ь < 0), — обратной. При прямой (обратной) связи увеличение одной из переменных ведет к увеличению (уменьшению) условной (групповой) средней другой. [c.58]
При г— корреляционная связь представляет линейную функциональную зависимость. При этом все наблюдаемые значения располагаются на прямой линии (рис. 3.3). [c.58]
Итак, между производительностью труда (Х ) и возрастом (А ) рабочих существует прямая корреляционная связь (/-12=0,20). Если же устранить (элиминировать) влияние переменной производственный стаж (Хт,), то в чистом виде производительность труда (Ai) находится в обратной по направлению (и опять же слабой по тесноте) связи с возрастом рабочих (Х2) (ri2.3=-0,26). Это вполне объяснимо, если рассматривать возраст только как показатель работоспособности организма на определенном этапе его жизнедеятельности. Подобным образом могут быть интерпретированы и другие частные коэффициенты корреляции. [c.130]
На развитие внешнеторговых отношений оказывает влияние множество различных факторов. Определить приоритетный ранг каждого из них достаточно сложно в силу отсутствия прямой корреляционной связи между абсолютными значениями каждого из факторов и конечным результатом, в качестве которого выступает объем внешнеторговых операций, уровень которого во многом определяется степенью развития внешнеторгового маркетинга. [c.229]
Так, статистическая связь между ценами пшеницы пекарного помола и оптовыми ценами на бирже определена коэффициентами корреляции (графа 10 табл. 14.5) со значением 0,837, а к ценам закупочным — в 0,742 (графа 14). В последнем случае менее тесная корреляционная связь может быть объяснена и таким аргументом, что эти цены формируются не непосредственно в виде прямого счета затрат. Между этапами фиксации этих цен имеется этап торговли на пшеничных биржах с участием торговых домов. [c.337]
Несмотря на разнохарактерность мероприятий по новой технике, даже в пределах одного направления научно-технического прогресса и при отсутствии прямых корреляционных связей [c.38]
| Рис. 1.7. Варианты прямых линий, выражающих прямолинейную корреляционную связь между зависимым показателем и параметром-аргументом | 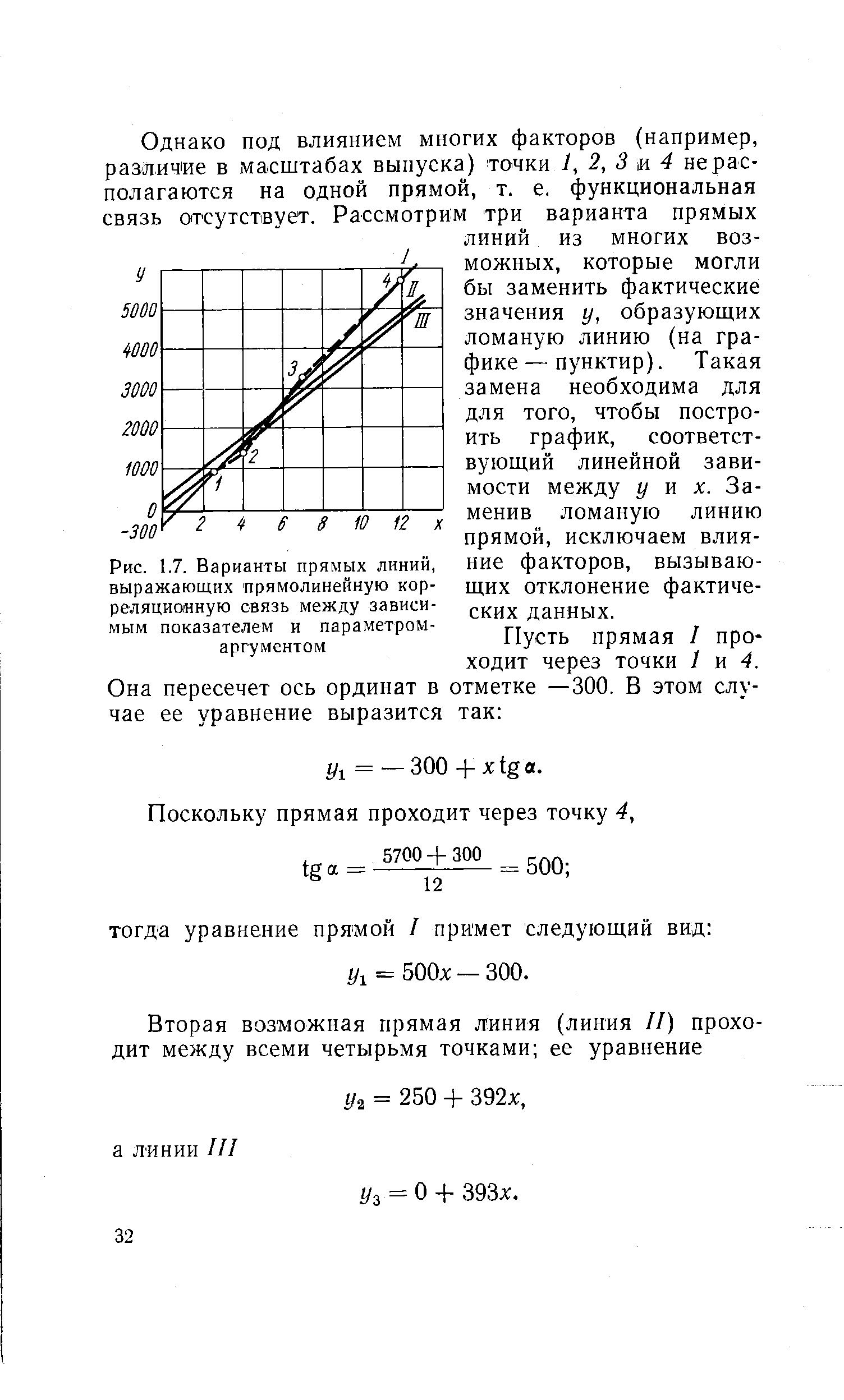 |
Уравнение корреляционной связи (уравнение регрессии) — аналитическое уравнение, с помощью которого выражается связь между признаками (иногда "форма связи"). Различают п р я м о л и н е й н о е (прямая линия) и к р и в о л и н е й н о е (парабола, гипербола) уравнения связи. [c.28]
Теснота связи определяется путем вычисления коэффициента корреляции. Отсутствие связи обозначается символом О, функциональная связь —1, а корреляционная связь — дробью со знаком плюс или минус. Таким образом, коэффициент корреляции г, во-первых, указывает на характер связи, т. е. имеется ли прямая (знак +) или обратная (знак —) связь во-вторых, он указывает на тесноту связи. Чем ближе коэффициент корреляции находится к единице, тем теснее связь, и, наоборот, приближение его к нулю характеризует низкую степень связи. Обычно считается, что коэффициент ниже 0,3 указывает на неустойчивую низкую степень связи, от 0,3 до 0,6 — а устойчивую среднюю степень связи, а выше 0,6 — на высокую степень связи. [c.268]
Сущность корреляционной связи состоит в том, что "разным значениям одной переменной соответствуют различные средние значения другой. С изменением значения признака X закономерным образом изменяется среднее значение признака Y..." [21, с. 192]. Проецируя данное положение на финансовую отчетность, можно в принципе вывести взаимосвязи между всеми статьями, установив направление и тесноту связи. Например, в ф. № 1 "Бухгалтерский баланс" и ф. № 2 "Отчет о прибылях и убытках" между строкой 210 "Запасы"(ф. № 1) и строкой 010 "Выручка..."(ф. № 2) существует положительная (прямая) связь, теснота которой (значение коэффициента детерминации от 0 до 0,33 от 0,33 до 0,67 от 0,67 до 1) зависит от количественных значений, а между строкой 020 "Себестоимость..." (ф. № 2) и строкой 010 "Выручка..." (ф. № 2) существует отрицательная (обратная) связь (в обоих случаях элиминировано влияние прочих факторов). Однако устанавливать корреляционную зависимость следует не по формам отчетности, а на основании данных синтетического учета. Полученные результаты послужат подтверждением правильности данных финансовой отчетности. [c.31]
Анализ вариантов хозрасчета наиболее полно реализуется при имитационном моделировании, в процессе которого предполагается выявить прямые и корреляционные связи между действием различных блоков и элементов хозрасчета и реакциями, которые эти действия вызывают в процессе производства. В ходе анализа определяется, какое взаимное влияние имеют управление и процессы воспроизводства, а также производственные системы различных уровней. Это придает анализу хозрасчета итеративный характер. Названные выше этапы аналитической работы, на наш взгляд, надо рассматривать как условную последовательность. [c.89]
Функциональная и корреляционная связь между показателями может быть прямой и обратной, прямолинейной и криволинейной. Однако экономические функциональные связи являются всегда многофакторными. Взаимосвязь между показателями обычно представляется в виде схемы или формулы. Например, для части показателей, влияющих на себестоимость перевозок ст общего объема перевозок Q0, удельного веса внутренних перевозок в общем их объеме YBT, средней дальности 1ср, произво- [c.23]
Корреляционные связи в зависимых переменных не могут быть жесткими и носят характер неполных связей. Если в случае увеличении (или уменьшении) аргумента результирующий показатель (функция) также увеличивается (или соответственно уменьшается), то корреляционная связь называется прямой (положительной), а если наоборот — обратной (отрицательной). При отсутствии какой-либо зависимости функции от аргумента, корреляционная связь отсутствует. [c.230]
Как пропорциональная, так и корреляционная связь между экономическими явлениями может быть прямой и обратной. Например, уровень себестоимости единицы продукции прямо зависит от величины затрат на 1 ед. продукции и обратно — от производительности. [c.35]
Недостаток оценки анализа уровня организации труда по частным коэффициентам состоит в том, что изменение этих показателей не имеет прямой связи с технико-экономическими показателями. Для установления такой связи пользуются методами корреляционного анализа. [c.129]
Значение коэффициента парной корреляции изменяется в пределах от -1 до +1. Знак + означает наличие прямой связи между показателями. Знак - — наличие обратной связи. Значение коэффициента от 0 до 1 характеризует степень приближения корреляционной зависимости между показателями и к функциональной. При р = 1 между показателями существует функциональная связь. При р = 0 линейная связь отсутствует. В целях упрощения расчетов на практике применяются и другие формулы коэффициента парной корреляции, представляющие собой некоторые преобразования исходной формулы. [c.280]
Корреляционно-регрессионный анализ учитывает межфакторные связи, следовательно, дает нам более полное измерение роли каждого фактора прямое, непосредственное его влияние на результативный признак косвенное влияние фактора через его влияние на другие факторы влияние всех факторов на результативный признак. Если связь между факторами несущественна, индексным анализом можно ограничиться. В противном случае его полезно дополнить корреляционно-регрессионным измерением влияния факторов, даже если они функционально связаны с результативным признаком. [c.232]
Если представить мультипликативную модель как двухфакторную, т.е. у = j , x2, то в целом по совокупности уравнение имеет вид у — ах. Коэффициент а является коэффициентом связи между у и х. Он передает прямое влияние фактора х на результат у. Для нашего примера величина отработанных человеко-часов передает влияние среднечасовой выработки на объем продукции. Однако выработка влияет на результат не только непосредственно, но и через другие факторы уровень выработки может определять численность рабочих, их долю в списочном составе, фактическую продолжительность рабочего дня. В корреляционном анализе, измеряя корреляцию между результатом и фактором, мы получаем полную меру корреляции независимо от того, как реализуется связь - непосредственно или опосредованно. В индексном анализе мы измеряем только прямое влияние изменения фактора на изменение результата. [c.403]
Снижение показателя дохода на одну акцию. В связи с тем что дивиденды выплачиваются из прибыли, уменьшение дохода на одну акцию понижает привлекательность акций для инвесторов и ведет к падению биржевого курса. Установлена прямая корреляционная зависимость (при нивелировании прочих факторов) между ростом курса акций и увеличением показателя дохода на одну акцию. [c.108]
При построении параметрических рядов машин, как и при любом экономическом анализе, недостаточно дать направление влияния (прямая, обратная связь) отдельных факторов на величину затрат, а необходимо знать и количественную сторону этого влияния. Конструкторы, чтобы изучить характер и степень влияния одних факторов на другие, производят наблюдения или опыт, измеряя значение одного фактора при разных значениях другого при условии постоянства значений прочих факторов. Экономист практически лишен возможности провести такой опыт. Поэтому только глубокий анализ отчетных и плановых данных позволяет ему выявить формы связи и степень влияния между факторами. Такой анализ может быть проведен с помощью методов математической статистики, а именно с помощью корреляционного анализа, который позволяет определить форму и степень влияния (тесноту связи) как отдельных факторов (в случае исследования парной зависимости), так и групп факторов (при исследовании множественной зависимости на исследуемую величину). [c.48]
Построение системы структурных уравнений позволяет глубже изучить причины связи, лежащие в основе вариации результирующих переменных. При этом происходят выделение и оценка косвенных (опосредованных) и непосредственных (прямых) влияний признаков. Именно поэтому системы структурных уравнений часто интерпретируются как статистические описания причинно-следственных связей, как причинные модели, объясняющие механизм формирования вариации выходных характеристик системы (результативных признаков). В случае использования аппарата корреляционно-регрессионного анализа структурное моделирование представляет собой попытку преодолеть косвенный характер изучения связей этим методом, подойти к выделению и измерению причинных связей переменных. [c.213]
Рассматриваемые связи математически описываются корреляционными уравнениями (другое название — уравнение регрессии). Напр,, простейшим корреляционным уравнением связи между двумя переменными является уравнение прямой вида у - в + Ъх, При функциональной связи такая прямая точно соответствовала бы всем значениям зависимой переменной. Если представить такую связь графически, то она проходила бы через все наблюдаемые точки у. При корреляции же соответствие, как указано, соблюдается лишь приблизительно, в общем, и точки наблюдений расположены не по прямой, а в виде "облачка", более или менее вытянутого в некотором направлении. Поэтому приходится специальными приемами находить ту линию, которая наилучшим образом отражает корреляционную зависимость, т.е. направление "облачка" (рис, К.1), Распространенный способ решения этой задачи — [c.155]
Рассеивание точек по всему полю любого из точечных графиков говорит о том, что отсутствует прямая (или обратная) корреляционная или функциональная связь в интервалах между объемом поставки и суммарным объемом суточных отпусков за интервал, т.е. с изменением суммарного объема суточных отпусков за интервал соответственно не увеличивается (или не уменьшается) объем поставки. Отсутствие связи подтверждают рассчитанные коэффициенты корреляции, они для данных по заводу Серп и Молот , Челябинскому тракторному заводу и тресту Железобетон находятся на уровне значительно меньшем, чем Л /и = 0,6. Только данные по Мурманскому рыбному порту несколько больше этого предела. При функциональной связи каждому суммарному расходу в интервале полностью соответствует производимый объем поставки, т.е. так отлажен процесс снабжения, что полностью следит за процессом расхода. И в данном случае все вышеуказанные точки, получаемые в процессе обработки, при построении легли бы на наклонную прямую и не было бы никакого их рассеивания. Пока таких случаев в организации процессов снабжения на предприятиях нам встречать не приходилось. [c.207]
Корреляционная функция связана со спектром мощности случайно-то процесса прямым и обратным прообразе [c.184]
Случайные изменения свойств сырья, а также ряда неконтролируемых факторов приводят к случайным колебаниям обеих исследуемых переменных. Однако расположение точек на рис. В. 6 свидетельствует о том, что эти колебания взаимосвязаны, подчинены вполне определенной закономерности облако рассеяния вытянуто вдоль некоторой прямой, не параллельной ни одной из координатных осей. Все это подтверждает целесообразность разложения случайной величины г) по формуле (В. 16) и исследования связи между г и 5, которая в этом случае носит название корреляционной. К перечисленным вопросам регрессионного анализа (построение конкретного вида зависимости между переменными, различные оценки ее точности) в этом случае присоединяется круг вопросов, связанных [c.40]
Коэффициент корреляции может принимать любые значения от 0 до 1. Если коэффициент корреляции равен нулю, то это означает отсутствие связи между х и у. Если его абсолютная величина составляет единицу, то, следовательно, существует полная зависимость между исследуемыми факторами, т, е, корреляционная зависимость совпадает с функциональной. Чем ближе коэффициент корреляции к единице, тем теснее зависимость между х и у чем ближе к нулю, тем связь слабее. Положительное значение коэффициента корреляции указывает на прямую зависимость, отрицательное значение — обратную. [c.115]
Корреляционное отношение имеет диапазон от 0 до 4-1 если п > г, то парабола точнее характеризует закономерность связи показателей, нежели прямая линия. [c.131]
Формы проявления взаимосвязей весьма разнообразны. В качестве двух самых общих их видов выделяют функциональную (полную) и корреляционную (неполную) связи. В первом случае величине факторного признака строго соответствует одно или несколько значений функции. Достаточно часто функциональная связь проявляется в физике, химии. В экономике примером может служить прямо пропорциональная зависимость между производительностью труда и увеличением производства продукции. [c.128]
Анализ корреляционной зависимости экономических показателей от отдельных факторов более сложен. Степень влияния таких факторов при анализе определяется с помощью методов корреляции. Связь между корреляционным фактором и результативным показателем характеризуется прежде всего коэффициентом корреляции, который может изменяться от нуля до единицы. Чем ближе он к единице, тем теснее связь между анализируемыми показателями. Коэффициент корреляции с плюсом указывает на прямую связь, а с минусом — на обратную. Коэффициент корреляции вычисляют по формуле [c.43]
Теснота связи между двумя показателями измеряется путем определения специального коэффициента корреляции (при прямой зависимости) или корреляционного отношения (при криволинейной зависимости). [c.228]
Факторы могут находиться во взаимной связи и взаимозависимости. Существуют два вида связи между взаимодействующими факторами и между факторами и показателями. Проще всего изучать функциональную, т, е. прямую или обратную зависимость, называемую также полной связью. Более сложной для исследования представляется корреляционная зависимость, называемая также неполной или частичной связью. Примером первого вида зависимости является связь между ценой товара и выручкой за товар. Примером второго — зависимость между иеной товара и его качеством. [c.23]
Этими лриемами вскрываются только наличие и направление связи. Но для того чтобы анализ имел практическое значение, одного выявления связи недостаточно. Связи бывают различны не только по направлению (прямая и обратная), но и по тесноте. Различают полные, или функциональные, и неполные, или корреляционные связи. Функциональной называется связь, при которой одному определенному значению аргумента соответствует одно определенное значение функции. Такие зависимости наблюдаются в области физики (например, закон Бойля-Мари-отта, по которому объем газа обратно пропорционален давлению). В общественных явлениях, а во многих случаях и в природе наблюдаются корреляционные связи, при которых одному определенному значению аргумента соответствует не одно, а несколько значений функции. В этом случае сопоставление между аргументным и функциональным рядами производится в форме средних величий. [c.268]
График корреляционной функции для минутных приращений индекса S P500 на основе ценовой динамики этого индекса 20 июня 1995 года представлен на Рис. 13. Корреляционная функция с временным лагом т, есть не что иное, как статистическая мера силы связи, с которой текущие изменения цены связаны с аналогичными приращениями цены на временном интервале т в прошлом. Такая функция называется автокорреляционной функцией, так как характеризует "память" изучаемого процесса, то есть ту меру причинности (линейной) которая содержится во временном ряду. Говоря другими словами, эта функция определяет, может ли быть предсказано будущее исходя из информации, заключенной в прошлых значениях. Сумма всех корреляционных функций для всех возможных временных лагов (от 1 до бесконечности), прямо пропорциональна числу случаев, когда будущие приращения цен будут близки их текущим приращениям по причинам, отличным от чистой случайности. Корреляционная функция равная нулю для всех ненулевых временных лагов подразумевает тот факт, что приращения являются случайными, как в игре в кости. Корреляция равная 1 соответствует абсолютному совпадению, которое наблюдается только для ценовых приращений сравниваемых сами с собой. Необходимо заметить, что нулевая корреляционная функция, не полностью устраняет возможность предсказания цен в будущем, поскольку другие алгоритмы обнаружения взаимосвязи, в частности, использующие, по крайней мере, три приращения (соответствующие, так называемой, "нелинейной корреляции") возможно лучше улавливают ценовую динамику. [c.48]
Главным экономическим показателем работы автотранспортного предприятия является прибыль, которая находится в прямой зависимости от себестоимости перевозок. В структуре себестоимости заработная плата водителей с начислениями составляет значительную величину. Так, за 1970 г. эти расходы по предприятиям Владимирского транспортного управления составили 31,9% к общей сумме расходов по грузовым сдельным автомобилям. В то же время снижение расходов по заработной платг может быть обеспечено при условии правильного установления плановых з а д а н и и по дайной статье себестоимости. Применяемые в настоящее время методы планирования заработной платы громоздки и не могут в полной мере учесть специфику отдельных предприятий. Они не позволяют быстро устанавливать величину заработной платы в зависимости от изменения размеров транспортной работы и других факторов, оказывающих на нее влияние. Использование метода цепных подстановок для анализа размера заработной платы также не дает желаемого результата. Корреляционный метод, особенно множественная корреляция, дает возможность количественно оценить связь между измеряемыми величинами в условиях действия большого числа факторов, причем некоторые из них неизвестны. Метод корреляции позволяет установить, как в среднем изменяется случайная величина при изменении значения одной или нескольких других случайных величин при фиксированном значении неучтенных факторов. [c.33]
В результате исследований для статистического моделирования инфляции был выбран один фактор - денежный агрегат М2 (в совокупности со скоростью его обращения). Выбор основан на приведенной выше эконометрическои модели и может быть подтвержден результатами корреляционно-регрессионного анализа. Наибольшие показатели тесноты связи оказались с агрегатом М2, кредитными вложениями в экономику (прямая зависимость) и [c.58]
КОРРЕЛЯЦИОННЫЕ ИСЧИСЛЕНИЯ В СТАТИСТИКЕ — строго математич. установление влияния фактора х на у на основе массового наблюдения, абстрагируясь от влияния других факторов, при прочих средних условиях. Корреляционная зависимость, в отличие от функциональной, характеризуется тем, что одному значению х соответствует ряд значений у в силу влияния других признаков. Примером корреляционной зависимости может служить зависимость между производительностью труда (выработкой) рабочих и их стажем, между производительностью труда и электровооруженностью труда, между общими затратами на произ-во и количеством вырабатываемой продукции и т. д. Рабочие с одинаковым стажем работы могут иметь различную выработку, т. к. на нее, кроме стажа, влияют и другие признаки. Вариация этих прочих признаков в каждом отдельном случае влечет за собой вариацию исследуемого признака. Связь между х и у определяется путем составления уравнений связи, или, как их называют, уравнений регрессии. Форма связи (прямолинейная или криволинейная) устанавливается на основе предварительного качественного анализа и в общем виде может быть представлена как yx=f(x), где F/v — среднее значение признака у при данном значении х и прочих средних условиях. Параметры уравнений регрессии находятся путем решения системы нормальных уравнений, отвечающих требованию способа наименьших квадратов. Так, для нахождения параметров прямой T/x=a0Jralx решается след, система уравнений [c.355]
Себестоимость перевозок хозяйств промышленного транспорта связана со многими показателями. При анализе этих связей различают прямые и обратные, прямолинейные и криволиней-. ные, однофакторные и многофакторные, функциональные и корреляционные. Из приведенного перечня последние имеют особое значение. Функциональной называют такую связь, когда каждому значению показателя (фактора)-аргумента соответствует строго определенное значение изучаемого показателя — функции. Так, при известных объеме перевозок и сумме эксплуатационных расходов получим вполне определенное, единственное значение средней себестоимости перевозок. [c.23]
Эти задачи обычно решаются путем прямых технико-экономических расчетов. Однако этот путь затрудняет рассмотрение большого числа факторов. В ряде случаев с его помощью можно выявить только тенденцию изменения показателя под влиянием, какого-либо фактора, но нельзя определить -количественную связь между ними. Большие возможности при решении таких задач имеют экономико-математические методы анализа. Ста-тистико-м атематический (корреляционный и регрессионный) анализ как одна из форм использования экономико-математических методов дополняет и углубляет изучение экономики производства и выявление резервов, достигаемое технико-экономическим анализом. Статистико-математический анализ позволяет выявить меру количественной зависимости экономических показателей от обусловливающих факторов между факторами. Он позволяет достаточно полно определить влияние каждого фактора на изучаемое явление и достигнуть относительно полного баланса и увязки факторов [26, 27 и др.]. [c.106]
КОЭФФИЦИЕНТ КОРРЕЛЯЦИИ, статистич. показатель, характеризующий силу (тесноту) связи двух (или большего числа) коррелирующих между собой случайных переменных. Исчисление К. к. предложено в конце 19 в. англ, учёными Ф. Гальтоном н К. Пирсоном. К. к. вычисляют только в том случае, когда сопоставляемые переменные подвержены лишь беспорядочным (случайным) изменениям, очищенным от присутствия зволюторных и периодпч. компонентов динамики (если данные расположены в последовательный ряд) или от явно выраженной неоднородности (если материал дан в форме корреляционной таблицы). Исчисление К. к. предполагает, что между переменными имеется н р я м о л и н е и н а я зависимость (прямолинейная регрессия) при иной форме уравнения регрессии К. к. тем больше теряет свою значимость, чем менее уравнение регрессии может быть представлено прямой. [c.275]
Корреляционная зависимость описывается уравнением, связывающим среднюю величину одного признака с другим и мерой её тесноты (коэфф. корреляции). Последняя показывает относит, долю в вариации зависимого признака той её части, к-рую можно отнести за счёт его связи с признаком-аргументом. Сама зависимость очень часто представляется в виде прямой линии (линейная корреляция). Пусть имеем по совокупности магазинов райпотребсоюзов признаки х — процент промтоваров в общем обороте и у — уровень издержек обращения (см. графы 1, 2, табл. 2). Допустив, что зависимость второго от первого может быть представлена как линейная, определяют параметры соответствующей линейной функции способом наименьших квадратов. Получим ух = 87—0,246 х. Если теперь определить средний квадрат отклонения от средней (общую дисперсию) заданных значений у, также теоретич. значений и средний квадрат отклонений одних от других ( остаточную дисперсию), то получим дисперсию эмпирич. значений D(y) = 61,5, выравненных D(yx) = 32,4 и остаточную, равную их разности — 29,1. [c.399]
Факторный анализ, как корреляционный анализ, сам по себе часто является промежуточной методикой, однако у него есть много прямых и ценных применений. Этот метод не рассматривает взаимоотношения между отдельными переменными, а находит группы аналогичных переменных. У этого метода есть очень ценные точки приложения. Там, где исследователь рынка раньше измерял большое количество переменных, они сокращаются до меньшего набора объединенных переменных. Каждая из этих объединенных переменных имеет то преимущество, что она независима от других и тем самым идеально подходит для применения в регрессии или кластерном анализе. В течение последних 10 лет факторный анализ стал фундаментом для обоснования серии тестов в рыночном исследовании ( hur hill and Peter, 1984). Он применяется либо в качестве своего рода разведки для выяснения того, какие переменные можно скомбинировать, либо в качестве подтверждения предположения связи между переменными. [c.108]
