Группировка производится с целью установления статистических связей и закономерностей, построения описания объекта, выявления структуры изучаемой совокупности. Различия в целевом назначении группировки выражаются в существующей в отечественной статистике классификации группировок типологические, структурные, аналитические. [c.122]
АНАЛИЗ И МОДЕЛИРОВАНИЕ Глава СТАТИСТИЧЕСКИХ СВЯЗЕЙ [c.226]
В настоящее время наука не знает более широкого определения связи. Все связи, которые могут быть измерены и выражены численно, подходят под определение статистические связи , в том [c.227]
Корреляционной связью называют важнейший частный случай статистической связи, состоящий в том, что разным значениям одной переменной соответствуют различные средние значения другой. С изменением значения признака х закономерным образом изменяется среднее значение признака у в то время как в каждом отдельном случае значение признака у (с различными вероятностями) может принимать множество различных значений. [c.228]
Статистическая связь между двумя признаками (переменными величинами) предполагает, что каждый из них имеет случайную вариацию индивидуальных значений относительно средней величины. Если же такую вариацию имеет лишь один из признаков, а значения другого являются жестко детерминированными, то говорят лишь о регрессии, но не о статистической (тем более корреляционной) связи. Например, при анализе динамических рядов можно измерять регрессию уровней ряда урожайности (имеющих случайную колеблемость) на номера лет. Но нельзя говорить о корреляции между ними и применять показатели корреляции с соответствующей им интерпретацией (см. гл. 9). [c.228]
Какое именно число явлений достаточно для анализа корреляционной и вообще статистической связи, зависит от цели анализа, требуемой точности и надежности параметров связи, от числа факторов, корреляция с которыми изучается. Обычно считают, что число наблюдений должно быть не менее чем в 5-6, а лучше - не менее чем в 10 раз больше числа факторов. Еще лучше, если число наблюдений в несколько десятков или в сотни раз больше числа факторов, тогда закон больших чисел, действуя в полную силу, обеспечивает эффективное взаимопогашение случайных отклонений от закономерного характера связи признаков. [c.230]
Вторая задача специфична для статистических связей, а первая разработана для функциональных связей и является общей. Основным методом решения задачи нахождения параметров уравнения связи является метод наименьших квадратов (МНК), разработанный К. Ф. Гауссом (1777-1855). Он состоит в минимизации суммы квадратов отклонений фактически измеренных значений зависимой переменной у от ее значений, вычисленных по уравнению связи с факторным признаком (многими признаками) х. [c.232]
Необходимость располагать данными за ряд лет делает статистическую оценку пока неприемлемой для большинства российских предприятий, акции которых не обращаются на рынке. Не годится он и для тех предприятий, акции которых котируются на фондовом рынке, поскольку, по наблюдениям экспертов РЦБ, выявленная статистическая связь и сильная изменчивость Р-коэффициента во времени определяются целенаправленным поведением профессиональных участников рынка, а не финансовым положением эмитентов. В настоящее время идет поиск новых методов оценки Р-коэффициента. [c.173]
По аналитическому выражению выделяют связи прямолинейные (или просто линейные) и криволинейные (нелинейные). Если статистическая связь между явлениями может быть приближенно выражена уравнением прямой линии, то ее называют линейной связью если же она выражается уравнением какой-либо кривой линии (параболы, гиперболы, степенной, показательной, экспоненциальной и т.д.), то такую связь называют нелинейной или криволинейной. [c.111]
Одновременно с корреляцией начала использоваться и регрессия. Корреляция и регрессия тесно связаны между собой первая оценивает силу (тесноту) статистической связи, вторая исследует ее форму. Обе служат для определения наличия или отсутствия связи между явлениями. [c.113]
Возникновение понятия статистической связи обуславливается тем, что зависимая переменная подвержена влиянию ряда неконтролируемых или неучтенных факторов, а также тем, что измерение значений переменных неизбежно сопровождается некоторыми случайными ошибками. Примером статистической связи является зависимость урожайности от количества внесенных удобрений, производительности труда на предприятии от его энерговооруженности и т.п. [c.51]
Корреляционной связью называется такая статистическая связь, при которой различным значениям одной переменной соответствуют разные средние значения другой. Возникать корреляционная связь может несколькими путями. Важнейший из них - причинная зависимость вариации [c.98]
Оценка статистической связи с влияющими параметрами. [c.123]
Оценка статистической связи с влияющими параметрами заключается в оценке связи прогнозируемого параметра с показателями, оказывающими на него непосредственное влияние (например, курс тесно связан с учетными ставками, биржевыми индексами, инфляцией, индексами потребления и безработицы и т. д.). Степень влияния их различна. Количественная оценка влияния статистическим методом реализуется следующим образом [c.123]
Уравнение статистической связи для оценивания коэффициента эластичности Э (р) импорта от соответствующих цен на импорт, а также для целей прогнозирования объемов продаж с учетом закупок по импорту, имеет следующий вид [c.115]
По приведенным данным оценка регрессионной зависимости Рц(руп), о которой говорилось выше, может быть представлена в виде корреляционного уравнения, исходя из какой-либо установленной формы статистической связи для всего выделенного интервала времени в 26 лет. Построение регрессий для более коротких временных периодов было бы ненадежным именно из-за небольшого объема выборки (малая выборка). [c.334]
Так, статистическая связь между ценами пшеницы пекарного помола и оптовыми ценами на бирже определена коэффициентами корреляции (графа 10 табл. 14.5) со значением 0,837, а к ценам закупочным — в 0,742 (графа 14). В последнем случае менее тесная корреляционная связь может быть объяснена и таким аргументом, что эти цены формируются не непосредственно в виде прямого счета затрат. Между этапами фиксации этих цен имеется этап торговли на пшеничных биржах с участием торговых домов. [c.337]
Математическая обработка данных и установление статистических связей между организационно-техническими факторами или результатами и технико-экономическими показателями. [c.191]
В случае статистической связи каждому значению одной величины соответствует определенное распределение вероятности другой величины. Это связано с тем, что в любой математической модели на описываемый показатель влияют не только явным образом входящие в модель переменные, но и большое количество факторов, которые существуют в действительности, но не учитываются моделью, причем часть из этих факторов -это случайные величины. Этим можно объяснить случайный характер многих финансовых переменных и взаимосвязей между ними. [c.91]
Важнейшим частным случаем статистической связи является корреляционная связь, когда каждому значению одной переменной соответствует определенное математическое ожидание другой переменной, и при изменении значения одной величины математическое ожидание другой величины изменяется закономерным образом. Если же при изменении значения одной переменной закономерным образом изменяется другая статистическая характеристика второй переменной (дисперсия, асимметрия, эксцесс и т.д.), то связь является статистической, но не корреляционной. Данная глава посвящена изучению линейной корреляционной связи между случайными величинами. [c.91]
Коэффициент Q находится в интервале значений —1. .. +1. Он может принимать значение нуль тогда, когда один из коэффициентов и 12 или п2 равен нулю. Абсолютное значение коэффициента Юла показывает степень статистической связи (или отсутствие таковой) для изучаемых пар величин. Чем ближе его модуль к единице, тем сильнее связаны измеряемые характеристики. [c.155]
Многие сопутствующие расходы при оценке капитальных затрат могут быть приняты как доля (в %) от расходов по основным статьям, что также является отражением существующих статистических связей. [c.153]
Итак, цель задачи — анализ статистической связи шести параметров полупроводникового прибора. Обозначим эти параметры Xi, xz, x3, 4> хь, хв. Между собой они причинно не связаны. В соответствии с нормами технических условий из общей массы выделялись годные приборы и анализировалась как вся масса приборов, так и годные. Это позволило попытаться уловить различие во взаимосвязи параметров приборов до и после их отбраковки. Эмпирические корреляционные отношения рассчитывались только для годных приборов, поскольку разброс параметров для всей совокупности приборов был настолько велик, что подсчитывать корреляционные отношения не имело смысла. Доверительные интервалы ввиду большого объема выборки подсчитывались по формуле [37]. Сравнение парных коэффициентов корреляции с эмпирическими отношениями использовалось для проверки линейности связи между параметрами. Эмпирическому корреляционному отношению приписывается тот знак, который имеет парный коэффициент корреляции. Связь считается линейной, если корреляционное отношение попадает в доверительный интервал для парного коэффициента корреляции. Может показаться, что мы противоречим высказанному выше утверждению о том, что не существует формальных методов, позволяющих определить форму связи. Однако в данном случае мы говорим не об определении формы связи с целью, например, нахождения параметров уравнения регрессии и дальнейшей интерпретации или экстраполяции в каком-либо виде. Единственная наша забота состоит в том, чтобы парные коэффициенты корреляции (или иные оценки тесноты связи) были действительными характеристиками связи. В табл. 94 приведены в первой строке каждой клетки — парный коэф- [c.188]
Регрессионный анализ выявляет также и статистические связи между переменными. Для этого выбирается измеритель связи (например, коэффициент корреляции), вычисляется его значение и проверяется правильность гипотезы о том, что полученное значение измерителя связи (например, значение коэффициента корреляции) действительно свидетельствует о наличии связи, а не является случайным, вызванным, скажем, флуктуацией измеряемых значений. [c.285]
Q = А2. Только В частном случае, Рис. 64. Варианты статистической связи когда случайные числа или вели- между двумя случайными числами [c.163]
Мерой статистической связи между значениями стационарного случайного процесса без постоянной составляющей в моменты времени /i и f2 = ti — т служит смешанный центральный момент 2-го порядка x(fi) x(ti — т), называемый корреляционным. Вероятностно-статистические характеристики стационарного случайного процесса не зависят от времени, поэтому ti можно выбрать произвольно, приняв 11 = t. Тогда корреляционный момент будет зависеть только от т. В силу эргодичности он равен [c.183]
| Рис. 71. Корреляционная функция стационарного случайного процесса Максимальное значение корреляционной функции при т = 0 объясняется тем, что статистическая связь между неразличимыми по времени значениями x(t) является наибольшей. Корреляционную функцию часто нормируют по ее максимальному значению г (т) — р (т) /р (0), тогда г (0) = 1. | 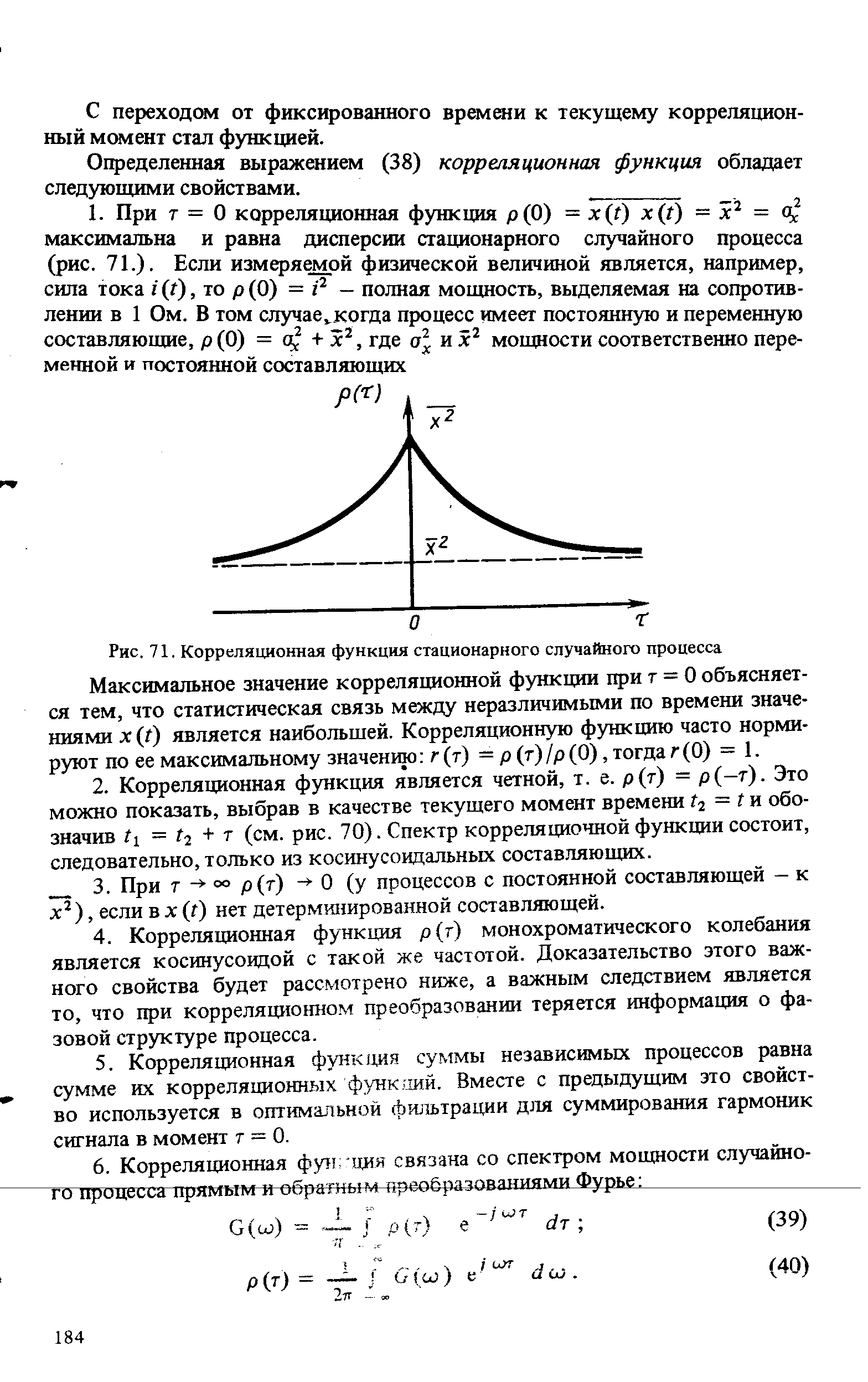 |
Этап 5 (анализ мультиколлинеарности предсказывающих переменных и отбор наиболее информативных из них.) Под явлением мультиколлинеарности в регрессионном анализе понимается наличие тесных статистических связей между предсказывающими переменными х(1 х(2),. .., х(р что, в частности, проявляется в близости к нулю (слабой обусловленности) определителя их корреляционной матрицы, т. е. матрицы размера р X р, составленной из парных коэффициентов корреляции rtj = r (x(i х(] )) ([14, с. 155], а также гл. 1—3 данного издания). Поскольку этот определитель входит в знаменатель выражений для ряда важных характеристик анализируемых моделей (см. гл. 7—11), то мультиколлинеарность создает трудности и неудобства при статистическом исследовании зависимостей по меньшей мере в двух направлениях [c.50]
Этап 6 (вычисление оценок неизвестных параметров, входящих в исследуемое уравнение статистической связи). Итак, в результате проведения предыдущих этапов были решены, в частности, следующие задачи [c.51]
СТАТИСТИЧЕСКОЙ СВЯЗИ МЕЖДУ ИССЛЕДУЕМЫМИ ПЕРЕМЕННЫМИ [c.56]
Стохастически детерминированная связь не имеет ограничений и условий, присущих функциональной связи. Если с изменением значения одной из переменных вторая может в определенных пределах принимать любые значения с некоторыми вероятностями, но ее среднее значение или иные статистические (массовые) характеристики изменяются по определенному закону - связь является статистической. Иными словами, при статистической связи разным значениям одной переменной соответствуют разные распределения значений другой переменной. [c.227]
Представляет собой метод установле мия связи и измерения ее тесноты между наблюдениями, которые можно считать случайными и выбранными из совокупности, распределенной по многомерному нормальному закону. Корреляционной называется такая статистическая связь, при которой различным значениям одной переменной соответствуют разные средние значения другой. [c.119]
Исследованиями доказано, что между этими циклами имеется статистическая связь через временной лаг, равный определенному средневероятному промежутку времени. Это лаг между моментом появления технического решения (либо между моментом оформления, регистрации технической идеи, проекта и т.д., например, получением патента на изобретение) и моментом максимального объема использования этой идеи, проекта и т.д. в промышленности. В связи с этим научно-техническая политика предприятия (фирмы) должна тщательно отслеживать отечественные и мировые тенденции развития науки и техники. Чтобы успешно решить эту задачу, нужно уметь анализировать потоки документов (информации). [c.86]
Возможность существования статистической связи между концентраци- [c.215]
Один из основных плюсов модели Shell/DPM состоит в том, что она решает проблемы объединения качественных и количественных переменных в единую параметрическую систему. В отличие от матрицы B G, она не зависит непосредственно от статистической связи между рыночной долей и прибыльностью бизнеса. [c.40]
СТАТИСТИЧЕСКАЯ СВЯЗЬ [statisti al interdependen e] — связь между переменными, на которую накладывается воздействие случайных факторов. В результате действия такой связи изменения одной переменной приводят к изменениям другой не детерминированно, как при функциональной связи (см. Функция), а статистически, отражаясь на изменении математического оэ/сидания последней. Такие взаимосвязи рассматриваются регрессионным анализом. Но может быть и так, что [c.344]
На практике обнаруживается, что как прямое, так и обратное следствие парадигмы СПЭ имеют большое значение. Этим можно объяснить незначимость статистической связи между концентрацией и прибыльностью возможно, это просто сумма двух эффектов с противоположными знаками. [c.162]
Менее освоенным (но не менее правомерным и актуальным) является этот подход в задачах оптимального регулирования характеристик социально-экономического поведения людей и целых коллективов в ситуациях, когда существует прин ципиальная возможность выявления статистических связей между этими характеристиками и набором объясняющих (и хотя бы частично регулируемых) факторов [40, 128] характеристик курса медицинского лечения структуры и объемов нагрузок и видов заданий в процессе профессиональной подготовки специалистов. [c.34]
Весь процесс статистического исследования зависимостей может быть разбит на семь последовательно реализуемых основных этапов, хронологический характер связей которых дополняется связями итерационного взаимодействия (см. рис. В.8) этап I (постановочный) этап 2 (информационный) этап 3 (корреляционный анализ) этап 4 (определение класса допустимых решений) этап 5 (анализ мультиколлине-арности предсказывающих переменных и отбор наиболее информативных из них) этап 6 (вычисление оценок неизвестных параметров, входящих в исследуемое уравнение статистической связи) этап 7 (анализ точности полученных уравнений связи). [c.55]
