Исследование объективно существующих связей между явлениями — важнейшая задача общей теории статистики. В процессе статистического исследования зависимостей вскрываются причинно-следственные отношения между явлениями, что позволяет выявлять факторы (признаки), оказывающие основное влияние на вариацию изучаемых явлений и процессов. Причинно-следственные отношения — это связь явлений и процессов, когда изменение одного из них — причины, ведет к изменению другого — следствия. [c.109]
Главная цель, которую ставили перед собой авторы, оснастить исследователя, использующего в своей работе статистические методы, инструментарием, необходимым для решения ключевой проблемы всякого исследования как на основании частных результатов статистического наблюдения за анализируемыми событиями или показателями выявить и описать существующие между ними взаимосвязи. Именно эта проблема, проблема статистического исследования зависимостей, оказывается главной в решении таких типовых задач практики, как нормирование, прогноз, планирование, диагностика, оценка труднодоступных для непосредственного наблюдения и измерения характеристик анализируемой системы, оценка эффективности функционирования или качества объекта, регулирование параметров процесса или системы. [c.6]
Читатель может познакомиться с этим аппаратом статистического исследования зависимостей, например, по книге [76]. [c.6]
И наконец, в раздел IV включены глава, посвященная описанию методов статистического анализа так называемых систем одновременных эконометрических уравнений (т. е. набора одновременно выполняющихся соотношений, в которых одни и те же переменные могут участвовать в разных соотношениях и в роли результирующего показателя, и в роли предсказывающей переменной), и глава, в которой дается обзор наиболее интересного отечественного и зарубежного программного обеспечения методов статистического исследования зависимостей. [c.7]
Любой закон природы или общественного развития может быть выражен в конечном счете в виде описания характера или структуры взаимосвязей (зависимостей), существующих между изучаемыми явлениями или показателями (переменными величинами или просто переменными). Если эти зависимости а) сто-хаотичны по своей природе, т. е. позволяют устанавливать лишь вероятностные логические соотношения между изучаемыми событиями А и 5, а именно соотношения типа из факта осуществления события А следует, что событие В должно произойти, но не обязательно, а лишь с некоторой (как правило, близкой к единице) вероятностью Я б) выявляются на основании статистического наблюдения за анализируемыми событиями или переменными, осуществляемого по выборке из интересующей нас генеральной совокупности [14, п. 5.4.2], то мы оказываемся в рамках проблемы статистического исследования зависимостей. Соответствующий математический аппарат, будучи таким образом нацеленным в первую очередь на решение основной проблемы естествознания как по отдельным, частным наблюдениям выявить и описать интересующую нас общую закономерность — занимает, бесспорно, центральное место во всем прикладном математическом анализе. [c.9]
Перед тем как перейти к формулировке общей и частных задач статистического исследования зависимостей, условимся описывать функционирование изучаемого реального объекта (системы, процесса, явления) набором переменных (рис. В.1), среди которых [c.9]
| Рис. В.1. Общая схема взаимодействия переменных при статистическом исследовании зависимостей | 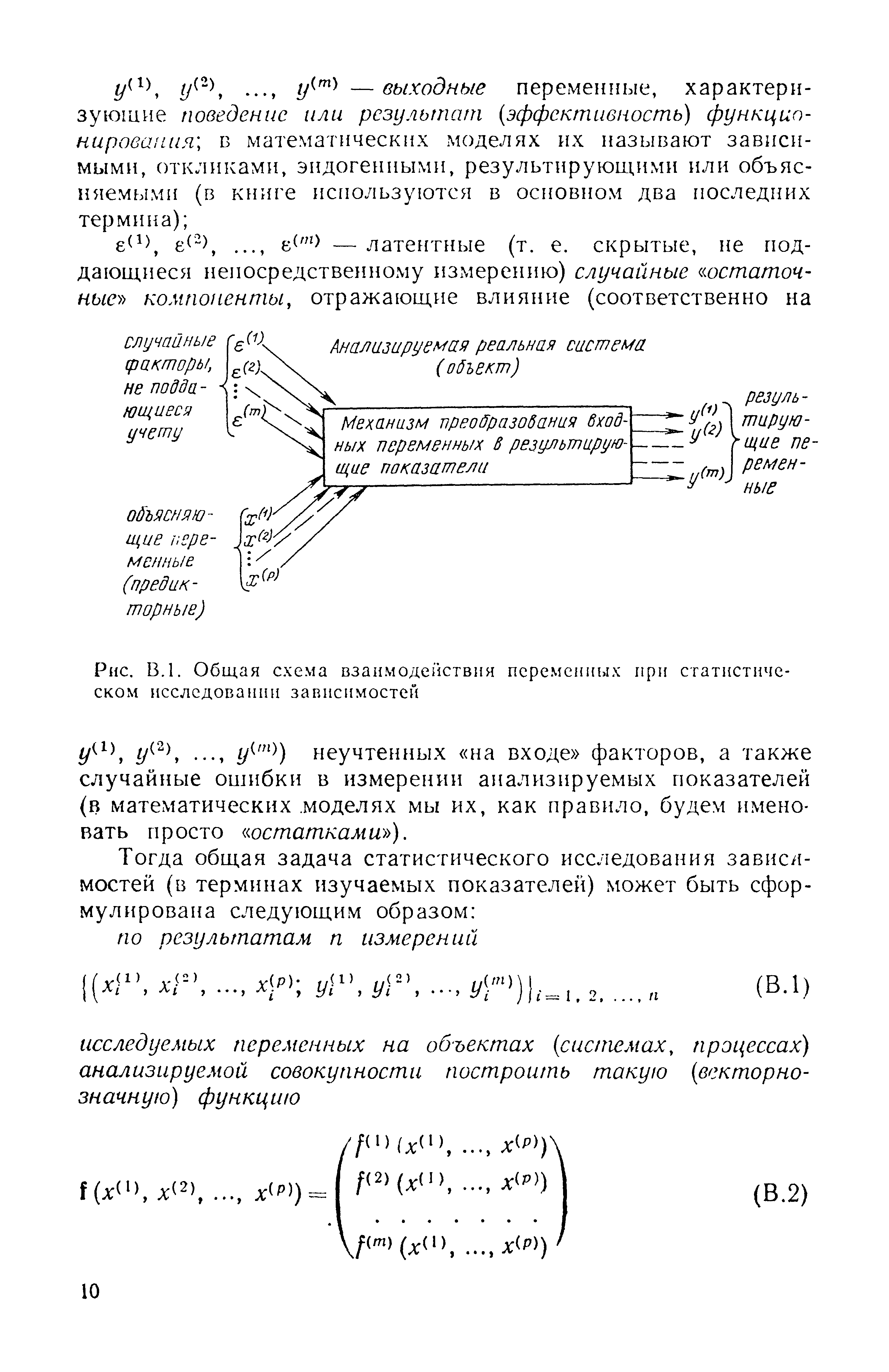 |
Вернемся к нашему примеру и попробуем ответить на некоторые из поставленных здесь вопросов, в том числе на принципиальные вопросы а), б) и в), ответы на которые позволяют уточнить общую формулировку задачи статистического исследования зависимостей, данную выше. [c.13]
И при выявлении причинных связей, и при намерении исследователя использовать модели типа (В.З) или (В.4) для управления значениями результирующих показателей Y p (X) или Y (X) путем регулирования величин объясняющих переменных X на первый план выходит задача правильного определения структуры модели (т. е. выбора общего вида функции f (X)), решение которой обеспечивает возможность количественного измерения эффекта воздействия на Y (X) каждой из объясняющих переменных х(1 х(2 . .., х(р) в отдельности. Однако как раз это место (правильный выбор общего вида функции f (X)) и является самым слабым во всей технике статистического исследования зависимостей к сожалению, не существует стандартных приемов и методов, которые образовывали бы строгую теоретическую базу для решения этой важнейшей задачи (некоторые рекомендации по проведению этого этапа исследования содержатся в гл. 6). [c.22]
Методы статистического исследования зависимостей составляют содержание отдельных частей многомерного статистического анализа, который можно определить [8, с. 731] как раз- [c.22]
Накопленный опыт практического использования аппарата статистического исследования зависимостей позволяет выделить те типы основных прикладных направлений исследований, в которых этот аппарат работает особенно часто и плодотворно. Если попытаться расщепить общую проблему оптимального управления сложной системой (т. е. центральную проблему кибернетики) на основные составляющие (рис. В.З), то [c.25]
| Рис. В.З. Основные направления практического использования аппарата статистического исследования зависимостей и центральная проблема кибернетики | 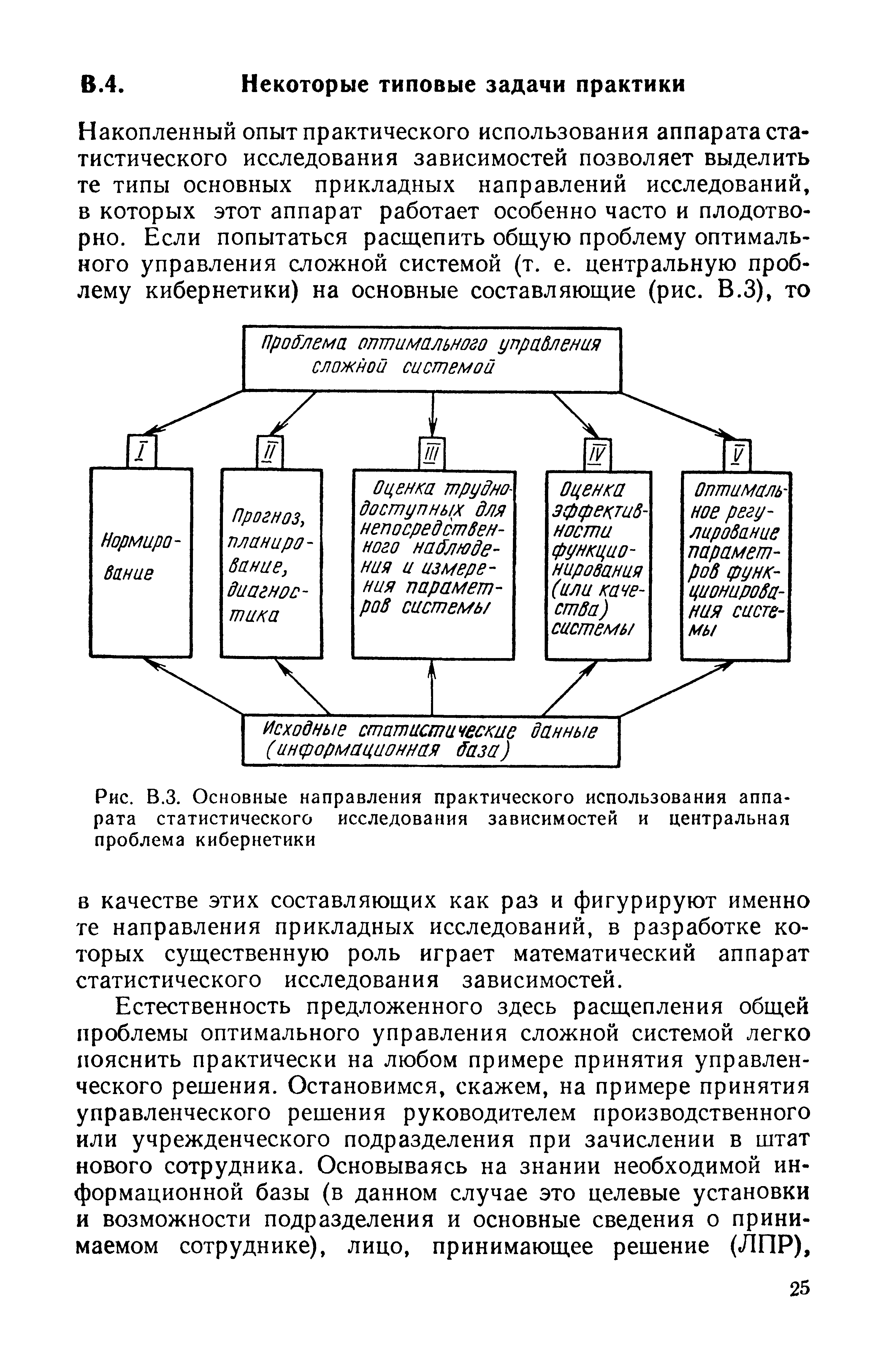 |
Имеется обширная литература по решению задач прогноза, планирования и диагностики с использованием аппарата статистического исследования зависимостей [4, 29, 31, 47, 80, 93, 128, 144, 152, 1631. В табл. В.З приведены примеры некоторых типичных задач этого направления прикладных исследований. [c.28]
Главная особенность (и трудность) описываемой ситуации заключается в том, что при получении (сборе) исходной статистической информации вида (В.1) значения результирующего показателя у могут быть получены только с помощью специально организованного экспертного опроса (значения частных критериев эффективности х(1 х(2 . .., х(р как правило, поддаются непосредственному измерению). Форма экспертной информации о значениях у может быть различной (балльные оценки, упорядочения, парные сравнения [11]). Но только располагая наряду со статистической информацией об X = (х(1>, х(2 . .., х(р)) одной из форм соответствующей экспертной информации об у, мы можем статистически построить некоторую аппроксимацию /Ср (X) — f (X 6) для агрегированного критерия эффективности функционирования системы и использовать ее затем в качестве формализованного метода оценки интегрального понятия эффективности (т. е. уже без привлечения экспертов, а лишь по частным критериям х(1 х(2 . .., х(р)). Такая модифицированная форма использования аппарата статистического исследования зависимостей предложена в [91, развита в [68] и носит название экспертно-статистического метода построения неизвестной целевой функции. [c.29]
Остается отметить, что и традиционные подходы аппарата статистического исследования зависимостей (классический регрессионный анализ, метод наименьших квадратов и т. п.) широко используются в практике оценки технического уровня и качества продукции. Это, в частности, отражено и в соответствующей официальной документации (см., например, РД 50 — 149 — 79 Методические указания по оценке технического уровня и качества промышленной продукции. Основные положения ГОСТ 22732 — 77 Методы оценки уровня качества промышленной продукции и др.). [c.33]
| Рис. В. 8. Схема хронологически-итерационных взаимосвязей основных этапов статистического исследования зависимостей | 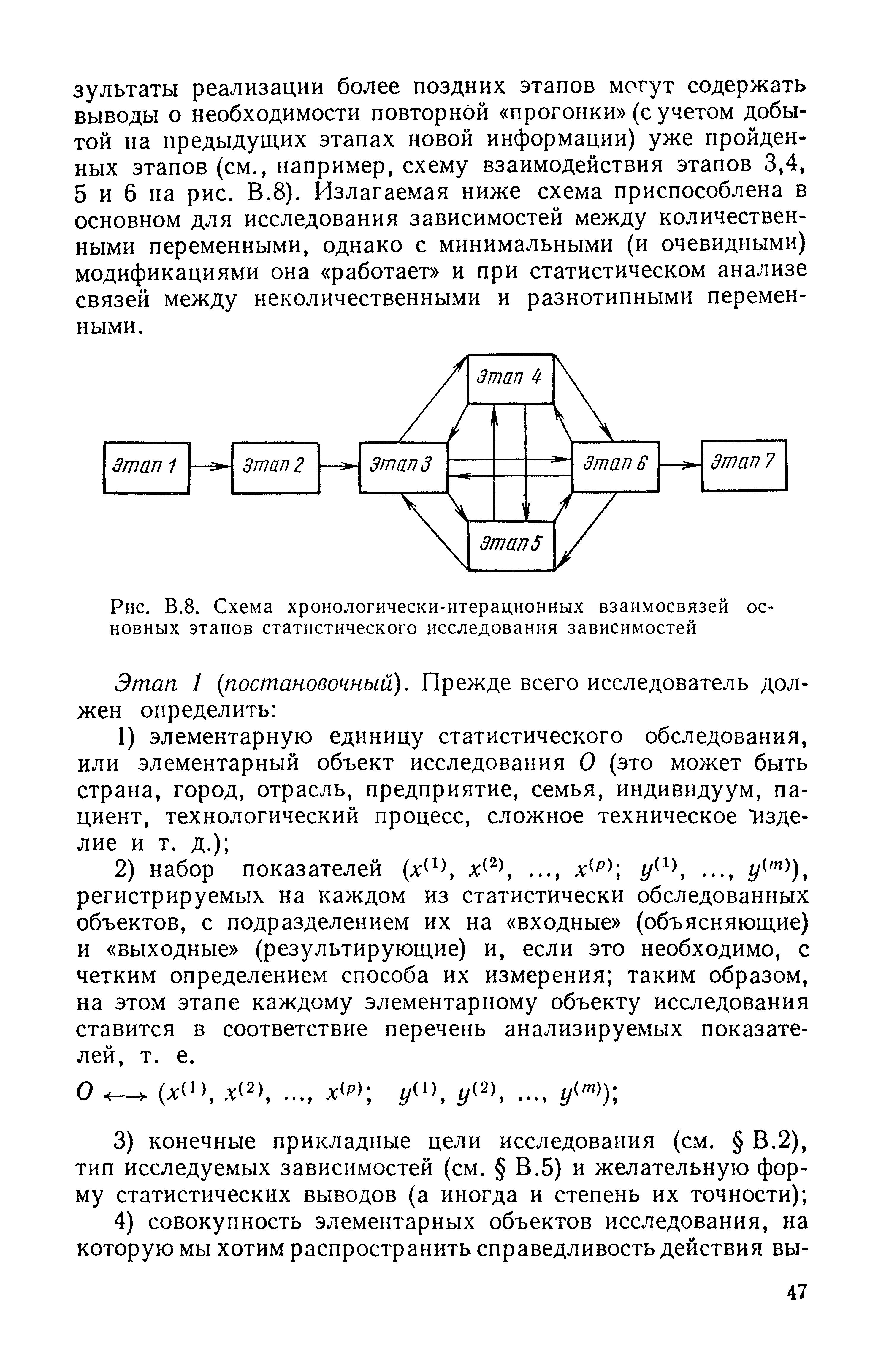 |
Аппарат статистического исследования зависимостей — составная часть многомерного статистического анализа — нацелен на решение основной проблемы естествознания как на основании частных результатов статистического наблюдения за анализируемыми событиями или показателями выявить и описать существующие между ними стохастические взаимосвязи. [c.53]
К основным типовым задачам практики, в которых использование аппарата статистического исследования зависимостей оказывается наиболее уместным и эффективным, следует отнести задачи 1) нормирования 2) прогноза, планирования и диагностики 3) оценки труднодоступных (для непосредственного наблюдения и измерения) характеристик исследуемой системы 4) оценки эффективности функционирования (или качества) анализируемой системы 5) регулирования параметров функционирования анализируемой системы. Все эти задачи являются основными составными частями центральной проблемы кибернетики — проблемы управления, связи и переработки информации (см. Математическая энциклопедия. Т. 2 — М. Советская энциклопедия, 1979, с. 850). [c.55]
Приступая к статистическому исследованию зависимостей между анализируемыми переменными, исследователь должен в первую очередь установить сам факт наличия статистических связей и попытаться измерить степень их тесноты. В качестве основных измерителей степени-тесноты связей между количественными переменными в практике статистических исследований используются индекс корреляции, корреляционное отношение, парные, частные и множественные коэффициенты корреляции, коэффициент детерминации. [c.97]
Предыдущий раздел (гл. 1—4) посвящен описанию математического аппарата, привлекаемого для реализации 3-го этапа статистического исследования зависимостей (см. Корреляционный анализ в п. В.6), на котором исследователь пытается проанализировать структуру связей между рассматриваемыми переменными и измерить степень их тесноты. После того как он убедится в наличии статистически значимых связей между анализируемыми переменными, он приступает к выявлению и математическому описанию конкретного вида интересующих его зависимостей подбирает класс функций, в рамках которого будет вести свой дальнейший анализ (этап 4) производит, если это необходимо, отбор наиболее информативных предсказывающих переменных (этап 5) вычисляет оценки для неизвестных значений параметров, участвующих в записи уравнения искомой зависимости (этап 6) анализирует точность полученного уравнения связи (этап 7). Этапы 4—7 и составляют содержание регрессионного анализа, описанию которого посвящен данный раздел. [c.164]
Во введении при общей формулировке задачи статистического исследования зависимостей (п.В.1), при описании основных прикладных проблем, в решении которых используется аппарат статистического исследования зависимостей (п. В.4), и при классификации основных типов исследуемых зависимостей (п. В.5) мы, по существу, уже использовали понятие функции [c.164]
Остановимся на конкретизации этого подхода применительно к задачам статистического исследования зависимостей и, в частности, к задаче наилучшего восстановления (по исходным статистическим данным вида (В.1)) условного значения результирующего показателя ц (X) = (ц = X) и неизвестной функции регрессии / (X) = Е (TJ = X). С этой целью воспользуемся следующей схемой рассуждений. [c.168]
Обратим внимание читателя на ряд частных случаев функции потерь р (и), широко используемых в теории и практике статистического исследования зависимостей [c.170]
Центральное место в аппарате статистического исследования зависимостей между количественными переменными занимает понятие регрессии результирующего показателя т] по объясняющим переменным Ъ>(1 <2>,. .., <Р>. [c.173]
Наряду с приведенным выше классическим определением функции регрессии в теории и практике статистического исследования зависимостей используются функции -регрессии, являющиеся наилучшими прогностическими моделями для анализируемого результирующего показателя rj (X) в смысле минимизации заданного критерия адекватности (агрегированной ошибки прогноза) Д (/а). Функции Д-регрессии позволяют подбирать наилучшие аппроксимации для неизвестной истинной функции регрессии. Кроме того, они представляют и самостоятельный интерес, позволяя строить и анализировать иную, чем условное среднее, условную характеристику места группирования результирующего показателя т) (X) = (г — X), обладающую в ряде ситуаций определенными преимуществами перед условной средней. [c.174]
УРАВНЕНИЙ И ПРОГРАММНОЕ ОБЕСПЕЧЕНИЕ АППАРАТА СТАТИСТИЧЕСКОГО ИССЛЕДОВАНИЯ ЗАВИСИМОСТЕЙ [c.401]
СТАТИСТИЧЕСКОГО ИССЛЕДОВАНИЯ ЗАВИСИМОСТЕЙ [c.425]
Методы статистического исследования зависимостей, в особенности регрессионный анализ, анализ временных рядов, дисперсионный анализ, анализ таблиц сопряженности, планирование эксперимента, наиболее употребительны среди методов обработки данных в различных областях науки и техники. Соответственно к настоящему времени существует и продолжает разрабатываться обширное программное обеспечение, связанное с исследованием зависимостей. Ниже кратко рассмотрены программные средства — пакеты и библиотеки программ, доступные пользователям в СССР, а также наиболее интересные, на наш взгляд, для обеспечения статистического исследования зависимостей зарубежные пакеты и библиотеки. Основные сведения о пакетах и библиотеках программ приведены в табл. 15.1. [c.425]
В табл. 15.2 приведены данные о разделах статистического исследования зависимостей, охватываемых пакетами и библиотеками программ. Номера вертикальных граф табл. 15.2 соответствуют следующим разделам и методам статистического исследования зависимостей [c.425]
Приведем теперь сведения о программном обеспечении некоторых разделов статистического исследования зависимостей, не включенные в табл. 15.1, 15.2. [c.426]
Заканчивая обсуждение примера В.1 и возвращаясь к общему описанию задач статистического исследования зависимостей,. отметим, что функции f (X) — Е (rj = X), описывающие поведение условных средних результирующего показателя 11 (вычисленных при значениях предикторных переменных , зафиксированных на уровне = X) в зависимости от изменения X, принято называть функциями, регрессии (подробнее о различных определениях функции регрессии см. в гл. 5). [c.19]
S. Нормирование. Общая схема формирования нормативов с использованием методов статистического исследования зависимостей может быть представлена следующим образом. Нормативный показатель играет в моделях типа (В.З)—(В.4) роль результирующей (объясняемой) переменной у, а факторы, участвующие в расчете нормативного показателя, — роль объясняющих (предикторных) переменных д (1>, л (2),. .., х(р). Предполагается, что привлечение для расчета норматива у полной системы определяющих его факторов, т. е. такой си- [c.26]
II. Прогноз, планирование, диагностика. Отправляясь от общей формулировки задачи статистического исследования зависимостей (см. В. 1) и от ее модельной записи (В. 11), определим в качестве результирующей переменной у интересующий нас прогнозируемый (планируемый, диагностируемый) показатель, а в качестве объясняющих (предикторных) переменных х(1), х(2 . .., х(р) — сопутствующие факторы, значения которых содержат основную информацию о величине этого показателя1. Наличие остаточной случайной компоненты [c.27]
Мы не случайно начали с этого примера. Использование методов статистического исследования зависимостей в задачах оптимального регулирования хода технологического процесса и построения соответствующих автоматизированных систем управления технологическими процессами (АСУТП) можно отнести к примерам грамотных и относительно распространенных актуальных приложений этого аппарата [47, 145]. Общая схема [c.34]
Центральным математическим объектом в процессе статистического исследования зависимостей является функция f (X), называемая функцией регрессии У по X и описывающая, как правило1, изменение условного среднего значения ср( ) результирующего показателя У (вычисленного при фиксированных на уровне X значениях объясняющих переменных) в зависимости от изменения значений объясняющих переменных X. [c.54]
Конечные прикладные цели статистического исследования зависимостей могут быть в основном трех типов 1) установление самого факта наличия (или отсутствия) статистически значимой связи между Y и X, исследование структуры этих связей 2) прогноз (восстановление) неизвестных значений индивидуальных или средних значений результирующего показателя по заданным значениям соответствующих объясняющих (предикторных) переменных 3) выявление причинных связей между объясняющими переменными X и результирующими показателями У, частичное управление значениями У путем регулирования величин объясняющих переменных X. [c.54]
Разделы многомерного статистического анализа, составляющие математический аппарат статистического исследования зависимостей, формировались и развивались с учетом специфики анализируемых моделей, обусловленной в первую очередь природой исследуемых переменных. Так, изучение зависимостей между количественными переменными обслуживается регрессионным и корреляционным анализами и анализом временных рядов (гл. 1 —12, 14), изучение зависимостей количественного результирующего показателя от неколичественных или разнотипных объясняющих переменных — дисперсионным и ковариационным анализами, моделями типологической регрессии (гл. 13) для исследования зависимостей в условиях активного эксперимента служит теория оптимального планирования экспериментов [2, 3, 136] наконец, для исследования системы зависимостей, в которых одни и те же [c.54]
Весь процесс статистического исследования зависимостей может быть разбит на семь последовательно реализуемых основных этапов, хронологический характер связей которых дополняется связями итерационного взаимодействия (см. рис. В.8) этап I (постановочный) этап 2 (информационный) этап 3 (корреляционный анализ) этап 4 (определение класса допустимых решений) этап 5 (анализ мультиколлине-арности предсказывающих переменных и отбор наиболее информативных из них) этап 6 (вычисление оценок неизвестных параметров, входящих в исследуемое уравнение статистической связи) этап 7 (анализ точности полученных уравнений связи). [c.55]
Имеется ли вообще какаях-либо связь между исследуемыми переменными, какова структура этих связей и как измерить их тесноту — эти вопросы исследователь ставит перед собой уже на ранней стадии статистического исследования зависимостей (см. описание этапа 3 в В.6). [c.56]
Статистическое исследование зависимостей в случае неколичественных переменных и переменных смешанной природы [c.426]
