Для стационарного случайного процесса дисперсия числа пересечений с положительной производной уровня х0 в единицу времени равна [c.228]
Стационарный случайный процесс 333 [c.490]
Полученные соотношения имеют смысл и в том случае, когда представляет собой стационарный случайный процесс с математическим ожиданием р0, дисперсией Dpo и плотностью распределения //(ро) на множестве V возможных значений р . Формула (7.53) для оптимального потока ресурса после перехода от усреднения по времени к усреднению по множеству примет вид [c.255]
Оценка вероятности истощения запаса ресурса. Для того чтобы выяснить, насколько грубой является полученная выше оценка (7.57), найдем вероятность истощения запаса ресурса A(t) в предположении, что ро(1) является гауссовым стационарным случайным процессом с корреляционной функцией вида [c.258]
Я г л о м А. М. Эффективные решения задач фильтрации и экстраполяции-стационарных случайных процессов. — Труды Московского математического общества , 1956, т. 4. [c.394]
Для стационарного случайного процесса, в частности, начальный момент первого порядка (среднее значение) определяется как [c.183]
Это так называемая постоянная составляющая стационарного случайного процесса (рис. 70), которую редко определяют, так как измерительная задача обычно заключается в выяснении динамики, развития явления. В дальнейшем будут рассматриваться случайные процессы с x(f) = О, т. е. без постоянной составляющей. [c.183]
| Рис. 70. Нормальный стационарный случайный процесс |  |
При т = 0 корреляционная функция р(0) = x(t) x(i) = Р = о максимальна и равна дисперсии стационарного случайного процесса (рис. 71.). Если измеряемой физической величиной является, например, сила тока г (г), то р(0) = г2 - полная мощность, выделяемая на сопротивлении в 1 Ом. В том случае. когда процесс имеет постоянную и переменную [c.184]
| Рис. 71. Корреляционная функция стационарного случайного процесса Максимальное значение корреляционной функции при т = 0 объясняется тем, что статистическая связь между неразличимыми по времени значениями x(t) является наибольшей. Корреляционную функцию часто нормируют по ее максимальному значению г (т) — р (т) /р (0), тогда г (0) = 1. | 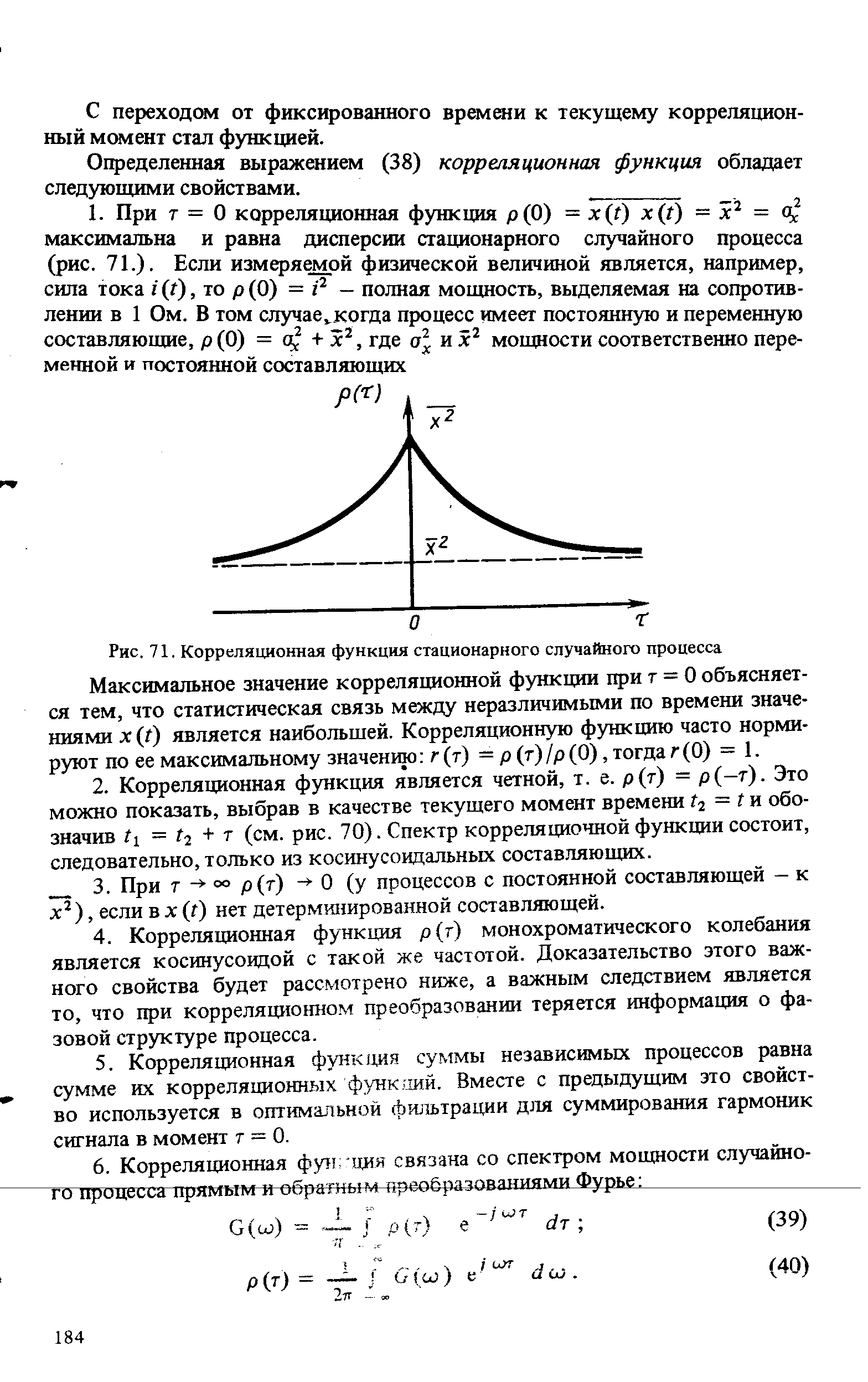 |
Если спектр мощности испытательного сигнала в виде стационарного случайного процесса известен, то [c.187]
Количественно свойство стационарности случайных процессов характеризуется следующими условиями. [c.106]
Постоянство математического ожидания, т.е. для стационарного случайного процесса [c.106]
Зависимость корреляционной функции процесса не от положения аргументов t, t на оси времени, а только от промежутка т = t — t между ними, т.е. для стационарного случайного процесса [c.106]
Таким образом, условие (2.116), устанавливающее зависимость корреляционной функции стационарного случайного процесса лишь от одного аргумента т, есть единственное существенное условие стационарности. [c.107]
Очень важной характеристикой стационарного случайного процесса является спектральная плотность, описывающая его (процесса) частотный состав. [c.107]
Спектром любого колебательного процесса, который может быть представлен в виде суммы гармонических колебаний различных частот (toд.), называется функция, описывающая распределение амплитуд но различным частотам ( гармоникам"). Амплитуды различных гармоник" стационарного случайного процесса являются случайными величинами. Следовательно, спектральная плотность Sx (со) случайного процесса описывает распределение дисперсий по его различным гармоникам и связана с корреляционной функцией преобразованием Фурье [c.107]
Чрезвычайно важным для решения практических задач свойством стационарных случайных процессов является их эргодичность. [c.108]
В экономич. исследованиях часто прибегают к использованию марковских и стационарных случайных процессов. Случайный процесс наз. марковским, если для любых двух моментов времени и
В теории стационарных случайных процессов относительно представления (15) для h =-(/in) принято говорить, что hn есть "результат реакции физически осуществимого фильтра с импульсной переходной функцией Ь = (bj), когда на вход подается последовательность е = (еп)" [c.155]
Не вдаваясь в математические подробности задач оценивания моментных характеристик стационарных случайных процессов, которые достаточно полно изложены в работах[25,26] отметим, что точность получаемых оценок зависит как от объёма используемых статистических данных, так и от сложности алгоритмов, используемых для их обработки. Если рассматривать отдельно проблему статистической обработки данных, то здесь представляется возможным использовать алгоритмы обработки любой сложности (степени оптимальности). Количество же имеющегося в распоряжении исследователя статистического материала (для конкретных [c.120]
Количественные характеристики портфеля ценных бумаг принято[8,9] рассматривать, исходя из предположений, что случайные величины, определяющие его эффективность, являются элементами генеральной совокупности с нормальным законом распределения. В терминах теории случайных функций [26] это эквивалентно понятию нормального стационарного случайного процесса (случайной последовательности). [c.125]
Из этого же допущения о стационарности случайного процесса исходят все методы авторегрессии, когда прогнозируемое значение параметра линейным образом зависит от некоторой совокупности предыдущих значений параметров [c.15]
Если i, ..., п, полученные в результате моделирования, зависимы, то приходится применять сложный аппарат. Последовательность рассматривают как значения стационарного случайного процесса (t) в равноотстоящие моменты времени т=0,1,.. Т. [c.77]
В процессах управления производством во многих случаях бывает очень важным уметь с достаточной степенью точности прогнозировать эти показатели. Имеется по крайней мере два метода, которые позволяют это осуществлять. Первый метод разработан А.Н. Колмогоровым. Сущность этого метода заключается в следующем. Прежде всего, этот метод распространяется на так называемые стационарные случайные величины, т.е. такие величины, у которых математическое ожидание [c.174]
Еще раз следует подчеркнуть, что для имитационных моделей, использующих случайные процессы, требование стационарности, отсутствия последействия, ординарности не является обязательным. Наоборот, случайные процессы реальных объектов в подавляющем большинстве случаев не отвечают вышеуказанным требованиям, и поэтому построение эффективной модели требует адекватного отображения этих процессов. [c.249]
Процесс скользящего среднего (МА). Стационарный стохастический процесс, где наблюдаемый временной ряд есть результат скользящего среднего ненаблюдаемого случайного временного ряда. МА(ц)-процесс представляет собой q-периодное скользящее среднее. [c.289]
Стационарность и эргодичность случайных процессов [c.106]
Следовательно, если случайный процесс нестационарен только за счет переменного во времени (по сечениям) математического ожидания, то операцией центрирования его всегда можно свести к стационарному. [c.106]
Например, пусть измеряемая величина представляет собой стационарный центрированный случайный процесс с заданной (определенной) автокорреляционной функцией R (т) или спектральной плотностью S( o) = [c.151]
В том случае, когда цены PQ и PQ представляют собой стационарные случайные процессы, полученные соотношения справедливы и могут быть обобщены, как это сделано выше для обмена с одним рынком. Для кинетики в форме (7.66) выражения (7.67) остаются в силе, если под PQ и PQ понимать математические ожидания этих процессов, а оценка для интенсивности получения прибыли (7.68) перепишется как [c.258]
Роза нов Ю. А. Стационарные случайные процессы. М., Физматгиз, 1963. [c.202]
Это интегральное уравнение, точнее, частный его случай, относящийся к стационарным случайным процессам и бесконечному наблюдательному времени, называется уравнением Винера — Хопфа. Решение его, принадлежащее области iQp, определяет оптимальную функцию веса линейного фильтра, который обеспечивает сглаживание (при /п = 0) и экстраполяцию (при п>0) по минимуму второго момента ошибок в соответствии с задачей (4.1). [c.312]
Как мы видели, в линейном случае формула (4.2) эквивалентна интегральному уравнению Винера — Хопфа (4.4) или (4.6). Уравнение Винера — Хопфа допускает конструктивное решение три стационарных случайных процессах т) ( ) и (i) с дробно-рациональными спектральными плотностями. Напомним, что спектральная плотность стационарного случайного процесса представляет собой преобразование Фурье его корреляционной. функции k(ti — 4). При таких предположениях о случайных процессах т]( ) и ( ) решение задачи (4.1) при бесконечном наблюдательном времени получено Н. Винером [69], а при конечном наблюдательном времени — Л. Заде и Л. Раггазини [121]. Другой подход к анализу этого случая предложен А. М. Ягломом [365]. [c.315]
Существуют два способа описа-ния случайных процессов. При пер-Т вом из них каждому текущему моменту времени t ставятся в соответствие случайные величины xt е < 1 п ПРИ втором — случайный процесс Q(t) задается множеством своих реализаций x(t) (рис. 69). Случайные величины х в каждом сечении t — onst подчиняются определенному закону распределения вероятности. Если он одинаков для любого сечения, т. е. не зависит от времени, то процесс называется стационарным в противном случае — нестационарным. Стационарные случайные процессы обладают свойством эргодичности, заключающемся в том, что вероятностные характеристики, вычисленные по множеству реализаций и по любой из них, равны между собой. Это позволяет при измерениях обходиться одной реализацией стационарного случайного процесса. [c.182]
Возможность измерения или вычисления по формуле (39) спектраль-ной плотности мощности стационарного случайного процесса используется для определения АЧХ средств измерений с линейной и стационарной ста- [c.186]
Кризис 2001 года явно дал понять, что ни о какой стационарности не может быть и речи. Поэтому теория Шарпа-Литнера также не выдержала испытания на прочность. Она (равно как и теория Марковица) хорошо работает в условиях неизменной парадигмы фондового рынка. В кризисные времена смены парадигмы, когда нестационарность ценовых процессов оказывается наиболее очевидной, столь же очевидной оказывается необходимость отказа от описаний, использующих стационарные случайные процессы. Эффект синхронной волатильности редуцируется, и инвесторы начинают приглядываться к возможностям роста или спада цены каждого конкретного актива, к фундаментальным параметрам эмитента. Возникает индивидуальный риск несовпадения фактической квартальной прибыли эмитента ожидаемым значениям, который зависит от рыночных условий хозяйствования эмитента. Этот риск порождает встречный риск оценочного понижения (downgrade) с вытекающим отсюда неизбежным падением цены акций. Таким образом рыночный риск актива теряет фундаментальный базис для измерения - рыночную линию, которая в условиях кризиса перестает существовать. Сейчас (ноябрь 2002 года) мы как раз наблюдаем поиски фондовым рынком США нового положения равновесия, новой рыночной линии. Однако эти поиски остаются тщетными, потому что еще окончательно не развеяны иллюзии инвесторов относительно справедливой цены активов, и целый ряд индустрии американской экономики по-прежнему являются переоцененными. Только при достижении окончательного дна фондовых индексов США можно говорить о формировании новой рыночной парадигмы и, соответственно - новой рыночной линии. [c.31]
Проверка условия р= 1 и. следовательно, наличия стационарного разностного процесса может быть выполнена с использованием проверки на единичный корень (unit root test). Если р = 1, то первое уравнение называют случайным блужданием с дрейфом. [c.129]
Большая часть работ по сглаживанию и прогнозу основана на предположении, что исходные случайные процессы, представляющие полезный сигнал и иомехи, стационарны. Это значит, по существу, что статистические -свойства сигнала и иомехи не меняются со временем. Другими словами, предположение стационарности означает, что статистические закономерности случайных процессов, установленные при изучении их поведения в прошлом, сохраняются и в будущем. Предположение стационарности, обычно приемлемое при решении технических задач, не может быть использовано для составления долгосрочных экономических прогнозов, для предсказания погоды на длительный период и для экстраполяции случайных процессов, порождающий механизм и тенденция развития которых недостаточно изучены. Методы сглаживания и упреждения стационарных процессов могут быть обобщены и для так называемых квазистационарных процессов, статистические характеристики которых медленно меняются во времени. В соответствии с теорией фильтрации и прогноза квазистационарных процессов могут быть построены сглаживающие и упреждающие фильтры с медленно изменяющимися параметрами, оптимальные для локальных статистик. Как мы увидим далее, ряд качественных выводов теории сглаживания и экстраполяции сохраняет силу и в нестационарном случае. [c.301]
Случайные процессы, протекающие во времени однородно, частные реализации которых с постоянной средней амплитудой калеблются вокруг средней функции, называются стационарными. [c.106]
Не всякий стационарный процесс является эргодичным, а лишь такой, частные реализации которого обладают одними и теми же характерными признаками (средним значением, размахом колебаний относительно среднего значения и др.), повторяющими на большом временном интервале все характерные особенности процесса. При этом каждая реализация несет на себе отпечаток" всей совокупности случайных явлений и факторов, формирующих случайный процесс, к которому она относится. В этом случае все характеристики процесса могут быть получены не по ансамблю реализации", а по одной (любой) из них, лишь бы ее длительность (временная протяженность) была достаточно большой (больше интервала корреляции). [c.108]
