Служба испытания, состоящая из определенного числа бригад, имеет определенную пропускную способность , под которой следует понимать среднее число скважин (заявок), которые могут быть испытаны в заданный промежуток времени. Если бы заявки поступали регулярно, через точно определенные промежутки времени и обслуживание каждой заявки тоже имело строго определенную длительность, расчет пропускной способности системы не представлял бы никакой трудности. На практике обычно момент поступления и длительность обслуживания заявок случайны, а поэтому и процесс функционирования системы представляет собой случайный процесс. Чтобы дать рекомендации по рациональной организации системы, выяснить ее пропускную способность и предъявить к ней требования, необходимо изучить случайный процесс, протекающий в системе, и описать его математически. [c.64]
В качестве критерия выбора наиболее рациональных величин s и q обычно используют математическое ожидание издержек в единицу времени. Для оценки зависимости этой величины от управлений s и q необходимо дать математическое описание потребления хранимого продукта. В теории управления запасами для описания спроса используют некоторые специальные классы случайных процессов, имеющие несложную структуру, что позволяет эффективно решить задачу выбора величин s и д. Например, в наиболее простом случае спрос описывают как случайный поток заявок на продукцию, причем для каждой заявки запрашивается [c.216]
Широкое распространение в экономическом анализе имеют методы математической статистики и теории вероятностей. Эти методы применяются в тех случаях, когда изменение анализируемых показателей можно представить как случайный процесс. Статистические методы [c.267]
Во-первых, вероятностный (стохастический) характер зависимости между многими экономическими показателями. Часто экономические явления отличаются особенностями случайного процесса. Например, уровень себестоимости добычи нефти и попутного газа оказывается под влиянием природных, производственных и организационных факторов. Однако в каждом отдельном случае влияние этих факторов неодинаково и результат их действия различный. Именно для таких случайных величин и процессов используются вероятностные методы исследования, одним из которых является корреляционный анализ. [c.59]
Г и к м а н И. И., Скороход А. В. Теория случайных процессов. М., Наука , 1971, 664 с. [c.124]
Теория массового обслуживания представляет собой прикладную область теории случайных процессов. Теория рассматривает вероятностные модели реальных систем обслуживания. Она используется для минимизации издержек в сфере обслуживания, в производстве, в торговле. При этом учитываются три фактора 1) ритм изменения числа клиентов, или заявок 2) вероятностные соображения, например, каковы шансы столкнуться с необычно большим наплывом покупателей 3) способ определения издержек ожидания и улучшения обслуживания. [c.74]
Не имея представления о возможных объемах выплат, практически трудно поддерживать устойчивый процесс страховой деятельности. Только статистико-математический аппарат позволяет описать случайные процессы и дать оценку ситуациям, складывающимся на реальном страховом поле с реальным страховым портфелем. [c.381]
Известно, что многие процессы, в том числе и экономические, представляют собой сочетание двух процессов детерминированного процесса (тренда) и случайного процесса. [c.450]
Статистические зависимости характеризуют взаимосвязи между функцией и аргументами, при которых значения последних меняются в каких-то пределах на основе случайных процессов, т.е. значения факторов имеют какую-то степень надежности. Поэтому стохастические зависимости относятся к приближенным методам, определяющим взаимосвязи функции и аргументов [11, 12]. [c.21]
Случайным процессом (или случайной функцией) Y(t) неслучайного аргумента t называется функция, которая при любом значении / является случайной величиной. [c.135]
Если исследуемый процесс у, в момент t определяется его значениями только в предшествующий период t — 1, то рассматривают авторегрессионную модель 1-го порядка (или модель AR (1) — марковский случайный процесс). [c.147]
Марковский случайный процесс 147 Матрица 258 [c.301]
Случайный процесс, протекающий в системе, называется марковским (по фамилии русского математика), если для любого момента времени вероятностные характеристики процесса в будущем зависят только от его состояния в данный момент и не зависят от того, когда и как система пришла в это состояние. Реально марковские случайные процессы в чистом виде в системах не протекают. Тем не менее реальный случайный процесс можно свести при определенных условиях к марковскому. А в этом случае для описания системы можно построить довольно простую математическую модель. [c.72]
Для многих экономистов эта идея показалась новой и странной. В действительности идея не была совершенно новой. Она была предложена в почти забытой докторской диссертации, написанной 53 годами раньше французом Луи Башелье. Предположение Башелье было достаточно оригинальным, а сопровождавшая его разработка математической теории случайных процессов на 5 лет опередила знаменитую работу Эйнштейна о хаотическом движении молекул инертных газов. [c.313]
В условиях неопределенности моделью динамики состояния банка может служить векторный случайный процесс [c.200]
Задача. Пусть в энергосистеме в течение пяти суток наблюдались следующие мощности спроса ( в 1000 мвт) за характерные часы суток 4, 10, 16, 19,24. Случайный процесс - спрос мощности. Требуются найти математические ожидания, М x(t), Dx(t), 5, Px(t, t) и на этой основе предсказать спрос в 19 часов, если в 10ч. утра спрос в 12000 мвт. (Рх (t,t )-коэффициент корреляции [c.10]
Процессы создания ПО определяют инвариант или неизменную составляющую процесса его разработки. Обычно разработка ПО не является результатом повторяющегося акта производства. Свойство случайности не присуще изначально ПО, скорее всего оно привнесено извне разработчиками. Свойства программной инженерии, носящие случайный характер, также порождают определенные трудности в создании ПО. Эти случайные процессы делятся на 3 категории 1. Участники проекта 2. Процесс 3. Язык и средства моделирования. [c.36]
Возможности рассмотренных стратегий и алгоритмов оптимального оперативного управления нефтеснабжением имеют определенные ограничения, обусловленные следующими обстоятельствами. JBo-первых, эти алгоритмы действуют только в условиях определенных заданных ресурсов. Во-вторых, решаемая модель построена в предположении стационарности случайных процессов поступления и ухода нефтепродуктов из системы, возможности усреднения времени движения по дугам сети, дискретности решения, постоянства критерия и др. В-третьих, модель не учитывает многих, часто неформализуемых внутренних и внешних взаимосвязей, которые в большой мере определяют условия и возможности работы системы и оказывают существенное влияние на выбор решения. [c.180]
Однако построение аппроксимирующих функций распределения путем проверки приемлемости различных статистических гипотез без предварительного анализа природы случайного процесса может дать далеко не лучшее приближение к реальным условиям, особенно, если речь идет об использовании этих распределений для прогнозирования. [c.258]
Для выбора аппроксимирующих функций необходимо возможно более детальное представление о закономерностях рассматриваемого случайного процесса и формирование обоснованных гипотез о его характере. [c.258]
Из всех параметров важнейшим, безусловно, является величина извлекаемых запасов. Но одновременно это и параметр, оценка которого представляет наибольшие трудности. В последние годы для прогноза размеров открываемых месторождений все больше используются статистические методы и методы имитационного моделирования. Используя гипотезу о логнормальном распределении размеров открываемых месторождений и метод Монте-Карло, можно имитировать случайный процесс открытий и генерировать совокупность месторождений. [c.157]
Во 2-й главе рассказано о наиболее употребительных законах распределения случайных величин и основных параметрах этих законов. Даны методы поиска функции распределения вероятности случайной величины в случае неинтегрируемой плотности вероятности, а также алгоритмы получения последовательностей случайных величин с произвольным законом распределения, что необходимо при моделировании случайных процессов. [c.10]
В этой главе мы рассмотрим наиболее употребительные законы распределения случайных величин, а также основные параметры этих законов. Будут даны методы поиска функции распределения вероятности случайной величины в случае неинтегрируемой плотности вероятности, а также алгоритмы получения последовательностей случайных величин с произвольным законом распределения, что необходимо при моделировании случайных процессов. Особое внимание будет уделено обобщенному экспоненциальному распределению, которое наиболее пригодно при изучении ценообразования активов. [c.30]
Встроенный в компьютер генератор псевдослучайных чисел выдает числа, равномерно распределенные в интервале от 0 до 1. С их помощью можно моделировать случайные процессы с произвольной функцией распределения. Подробнее о том, как это делается, будет рассказано далее в этой главе. [c.34]
Из вышесказанного следует, что аппроксимация распределением Коши случайных процессов, которые характеризуются конечным математическим ожиданием и конечной дисперсией, неправомерна. [c.40]
Движение цены актива - это случайный процесс, вызванный действиями большого количества участников рынка. Предположим, что отношения цен активов в любой момент времени являются случайными величинами с одинаковым законом распределения. [c.84]
Другой тип случайного процесса характеризуется тем, что результат предыдущих событий влияет на значение вероятности, и, таким образом, значение вероятности непостоянно от одного события к другому Эти виды событий называются процессами зависимых испытаний (отбор без замещения). Игра 21 очко является примером такого процесса. После того как вытаскивают карту, состав колоды изменяется. Допустим, что новая колода перемешивается и одна карта удалена, скажем, бубновый туз. До удаления этой карты вероятность вытянуть туза была 4/52, или 0,07692307692. Теперь, когда туза вытащили из колоды и не вернули обратно, вероятность вытянуть туза при следующем ходе составляет 3/51, или 0,05882352941. [c.15]
Одно из наиболее важных применений нормального распределения относится к распределению средних значений. Средние значения выборок заданного размера, взятые таким образом, что каждый элемент выборки отобран независимо от других, дадут распределение, которое близко к нормальному Это чрезвычайно важный факт, так как он означает, что вы можете получить параметры действительно случайного процесса из средних значений, рассчитанных на основе выборочных данных. [c.90]
Таким образом, можно ожидать, что 97,72% результатов в нормально распределенном случайном процессе не попадают за +2 стандартные единицы. Это изображено на рисунке 3-8. [c.96]
Таким образом, с вероятностью 2,275% событие в нормально распределенном случайном процессе будет равно или превышать +2 стандартные единицы. Это показано на рисунке 3-9. [c.96]
С помощью рассмотренных в этой главе математических подходов вы сможете рассчитывать любые вероятности событий для случайных процессов, имеющих нормальное распределение. [c.99]
Однако не надо забывать, что хотя цены акций в среднем растут, но акции каждой отдельной компании вполне могут и падать. Существуют сотни примеров, когда акции, стоившие десятки долларов, падали до нескольких центов. Если просмотреть графики зависимости цен акций различных компаний от времени, то может сложиться впечатление, что на коротком промежутке времени (месяцы или год) движение цен совершенно случайно. Что произойдет с акциями завтра, не зависит от того, что было с ними сегодня, вчера и т.д. Вероятности падения или роста цены на следующий день представляются практически равными. Если это так, то поведение цены акций — это случайный процесс, и игра на бирже мало отличается от игры в казино полный хаос и все решает случай. К тому же, покупая акции, вы платите комиссионные брокеру и дополнительно теряете деньги на разнице цен покупки и продажи. В таком случае, даже если вероятность выигрыша и проигрыша одинакова, то в среднем вы проиграете за счет указанных затрат. [c.47]
| Рисунок 2. Проявляющееся по мере погружения ряда различие между случайным процессом и хаотической динамикой | 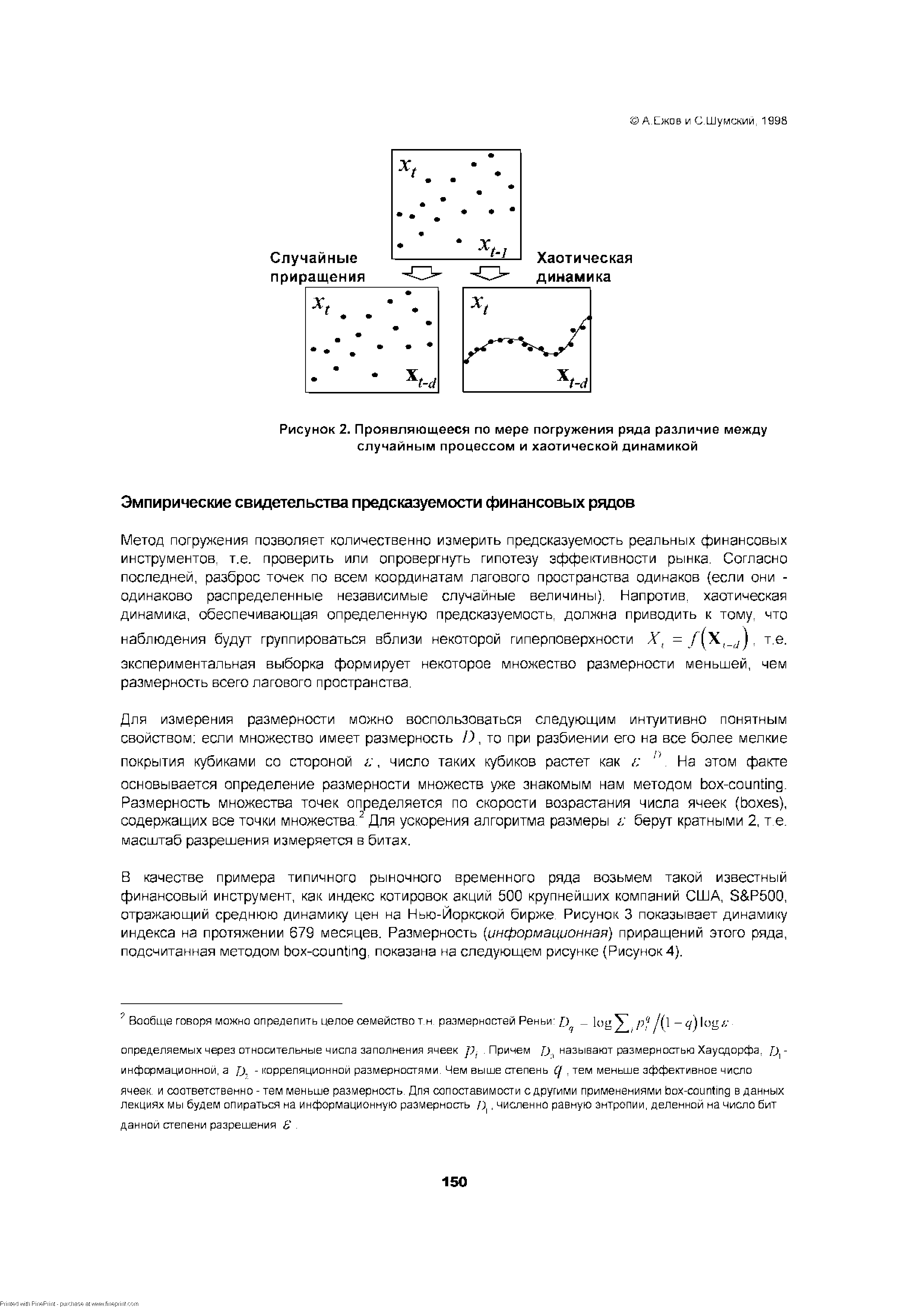 |
Математическая статистика находит наибольшее применение при анализе хозяйственных процессов и явлений в их становлении и развитии. Этот метод анализа используется в тех случаях, когда изменение изучаемых явлений можно представить как случайный процесс. Статистические приемы, предназначенные в основном для изучения массовых, эпизодически повторяющихся явлений, имеют весьма важную роль при прогнозировании изменений изучаемых показателей на близкую и далекую перспективу. Наиболее распространенным среди них в настоящее время является метод корреляции, по названию которого утвердился и применяется особый вид анализа — корреляционный. [c.20]
Широкое распространение в экономическом анализе имеют методы математической статистики. Эти методы применяются в тех случаях, когда изменение анализируемых показателей можно представить как случайный процесс. Статистические методы, являясь основным средством изучения массовых, повторяющихся явлений, играют важную роль в прогнозировании поведения экономических показателей. Когда связь между анализируемыми характеристиками не детерминированная, а стохастическая, то статистические и вероятностные мето- [c.94]
Гемиктери В. И., Френкель А. А. Прогнозирование случайных процессов с помощью авторегрессионных моделей.—Заводская лаборатория, 1967, № 7, с. 853—858. [c.227]
Как можно заметить, основным принципом для pa 4eTa RSI является теория вероятности. На основании применения этой теории можно сказать, что не может цена подниматься бесконечно долго, также как и опускаться. Можете проверить это положение на абсолютно случайном процессе - подбрасывании монетки с двумя исходами такого подбрасывания "орлом" и "решкой". [c.92]
Смотреть страницы где упоминается термин Случайный процесс
: [c.142] [c.218] [c.218] [c.452] [c.219] [c.71] [c.152] [c.10] [c.50] [c.50] [c.97] [c.97]Экономико-математический словарь Изд.5 (2003) -- [ c.332 ]
