Сущность дискриминантного анализа близка к сущности регрессионного. Целью применения данного метода является аппроксимация распределения наблюдаемых объектов по значениям изучаемого качественного показателя. Для этого строится регрессионная функция по количественным факторным показателям таким образом, чтобы можно было найти определенное критическое значение (дискриминант) данной функции, которое отмечает границу распределения по качественному показателю. [c.109]
Обозначим qj вероятность прибытия j новых требований за время обслуживания. Нетрудно видеть, что qj определяются согласно (3.6.3) и при аппроксимации распределения времени обслуживания гамма-плотностью проблем с их вычислением не будет. В установившемся режиме застать в системе k требований в очередной момент регенерации можно, если в ней [c.94]
Пакет использует фазовую аппроксимацию распределений и непосредственно вызывает 21 процедуру МОСТа. Всего в него входят 50 процедур (их список был построен автоматически как транзитивное замыкание первичного). [c.117]
Такая универсальность позволяет использовать одни и те же математические формулы при исследовании самых различных потоков отказов изделий. Кроме того, этот закон удобен при аппроксимации статистических данных, так как распределение вероятностей безотказной работы изделий может быть сведено к линейной функции, что позволит довольно просто определять параметры распределения. [c.63]
Результаты решений по различным интервалам аппроксимации (см. табл. 86) могут быть отнесены в одну группу по значениям функционалов, различающихся не более чем на 2—3%. Если этот процент считать соизмеримым с погрешностью определения нормативов, то в качестве решения нелинейной задачи можно принять оптимальный план любого интервала, отвечающего максимальным значениям функционалов (с принятой точностью). Это позволяет выбрать такой план, реализация которого на месторождении была бы наиболее целесообразна, например вместо пикового разбуривания месторождения — плановое (распределенное по годам периода разбуривания). [c.228]
АППРОКСИМАЦИЯ ПЛОТНОСТИ РАСПРЕДЕЛЕНИЯ СДАЧИ НЕФТЕПРОДУКТОВ НЕФТЕПЕРЕРАБАТЫВАЮЩИМ ЗАВОДОМ И ПОТРЕБЛЕНИЯ НЕФТЕПРОДУКТОВ [c.257]
Хотя рассматриваемые распределения вероятностей являются хорошей аппроксимацией реально наблюдаемых на рынке распределений, трудно ожидать, что рыночные цены опционов будут столь строго отвечать данному симметричному распределению. Однако для нас пример интересен как иллюстративный. [c.29]
Распределение логарифмов уже может быть симметрично и возможна его аппроксимация одним из аналитических законов распределения, которые были рассмотрены во второй главе. [c.85]
Новый подход лучше, так как исходные данные теперь уже не располагаются вдоль линий ожидаемых доходов и (достаточно расплывчатой) дисперсии ожидаемых доходов или какой-то другой эрзац-меры риска. Аргументами новой модели являются различные сценарии возможных исходов инвестирования (более точная аппроксимация реального распределения дохода). Теперь, в отличие от оценок таких величин, как ожидаемые доходы и их дисперсии, исходная информация гораздо ближе к тому, чем может мысленно оперировать менеджер по инвестициям, например, 5%-ная вероятность выигрыша или потери в х%, и т.д. Теперь за аргументы новой модели менеджер по инвестициям может принимать даже неестественно маловероятные сценарии. [c.28]
В действительности, распределения приращений цен не является гауссовским, как показано на Рис. 17. Если бы это было так, то должно было проявиться в виде перевернутой параболы на этом полулогарифмическом графике. Линейная аппроксимация наблюдаемой зависимости скорее может интерпретироваться как зависимость, приближающаяся к экспоненциальному закону. В этом новом улучшенном представлении, мы можем снова вычислить вероятность наблюдения амплитуды приращения большей, чем, скажем, 10 стандартных отклонений (10% в нашем примере). Результат - 0.000045, который соответствует одному событию за 22,026 дня или 88 лет. Рост цен 20 октября 1987, в свете этого, становится менее экстраординарным. Однако, падение цен на 22.6% 19 октября 1987 соответствовало бы одному случаю за 520 миллионов лет, что позволяет интерпретировать его как " выброс". [c.62]
Что касается финансовых временных рядов, то большой интерес представляет распределение скорости изменений между двумя мгновениями в той же самой позиции или между двумя точками одновременно. Такое распределение для квадрата скорости изменений показано Рис. 22. Обратите внимание на аппроксимацию экспоненциального снижения, представленную прямой линией и на сосуществование больших колебаний справа для значений от 4 до 7 и далее, (которые не показаны). Обычно, такие большие колебания считаются статистически не значимыми и не добавляют никакого дополнительного понимания. Здесь можно показать, что эти большие колебания скорости жидкости соответствуют интенсивным пикам, когерентно распространяющимся через несколько корпусных слоев с колоколообразной характеристикой, почти независимой от их амплитуды и продолжительности (даже при перемасштабировании их размера и продолжительности). При продлении наблюдений на значительно более длинный период, чтобы аномальные флуктуации, большие значения 4 на Рис. 22 могли бы быть смоделированы намного лучше, мы получаем непрерывные кривые (кроме некоторого постоянного остаточного шума), показанные на Рис. 23. Здесь, каждая из трех кривых соответствует измерению распределения в данном корпусном слое (п = И, 15, и 18). [c.69]
Аппроксимация получалась более грубой в области хвостов распределения, т.е. там, где значения переменной наиболее далеки от среднего. Это могло привести к некоторым искажениям в наших тестах. Мы, однако, игнорируем это обстоятельство, поскольку тесты нам нужны только для того, чтобы проиллюстрировать возможности нейронных сетей. [c.95]
| Рис. 6.2. Интегральная зависимость вероятность — ущерб и ее аппроксимация нормальной функцией распределения | 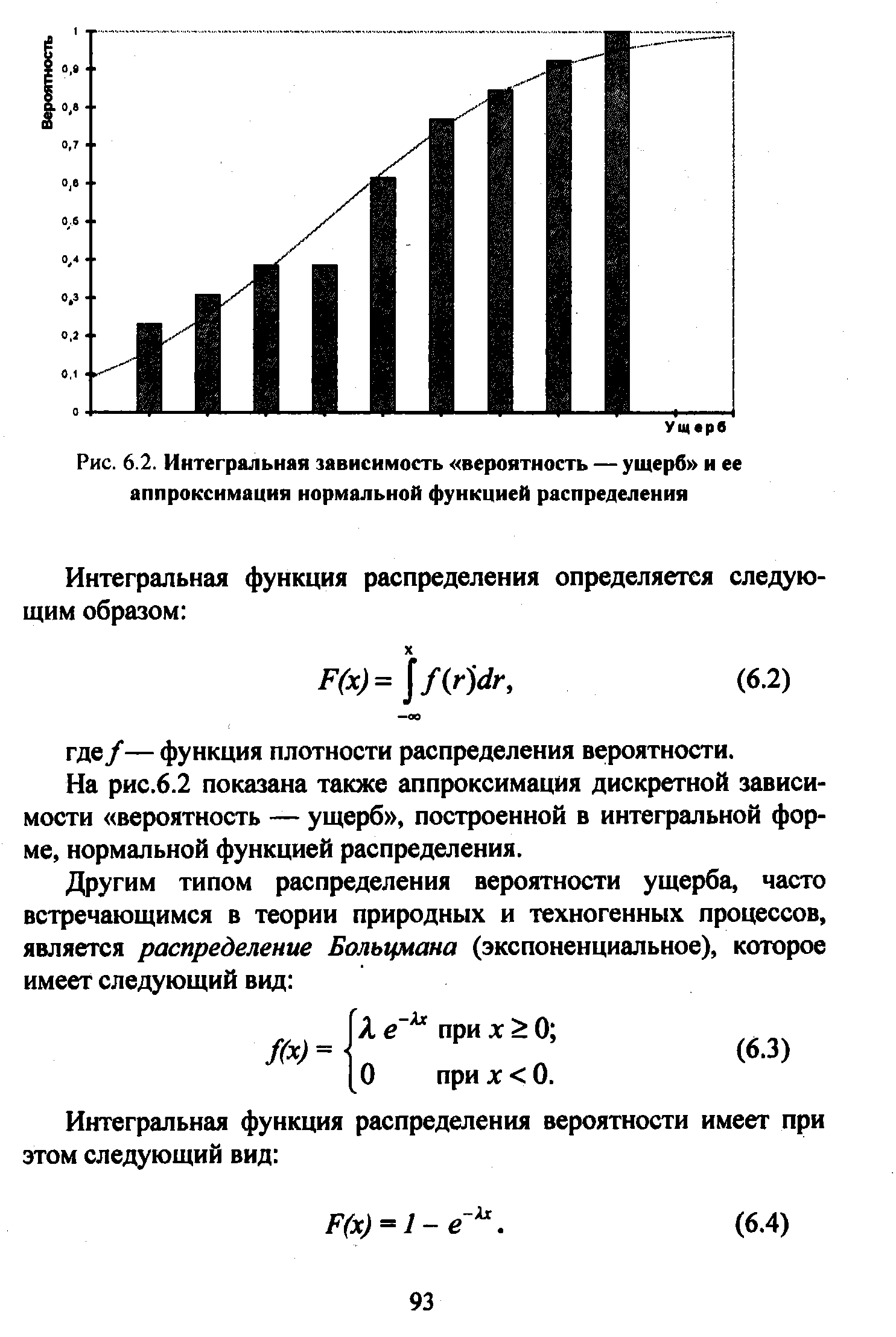 |
Первым этапом этого алгоритма является начальное распределение (составление начального плана перевозок). Для этого имеется ряд методов северо-западного угла, наименьших стоимостей, аппроксимаций Фогеля и др. Второй этап — построение системы потенциалов на основе равенства (25.33), а третий — проверка начального плана на оптимальность, причем в случае его неоптимальности переходят к четвертому этапу, содержание которого заключается в реализации так называемых циклов перераспределения плана прикрепления потребителей к поставщикам, после чего переходят опять к третьему этапу. Совокупность процедур четвертого и третьего этапов образует одну итерацию, и эти итерации повторяются, пока план перевозок не окажется оптимальным по критерию (25.29) [c.526]
Пример 5. Предположим, что спрос в примере 1 в действительности представляет собой аппроксимацию случайной ситуации, при которой ежедневный спрос распределен нормально со средним ц= 100 и [c.556]
Решающие правила и характеристики решающих распределений могут определяться как непосредственно по статистическим характеристикам исходной информации, так и в результате итеративного процесса обучения по последовательным реализациям наборов случайных параметров условий задачи. Формальный аппарат итеративного совершенствования решающих правил и характеристик решающих распределений представляет собой естественное обобщение стохастической аппроксимации. В задачах немалых размеров рациональный выбор начального приближения для решающих правил и решающих распределений, основанный, как правило, на неформальных содержательных соображениях, является важнейшим условием получения удовлетворительного приближения за приемлемое время. [c.6]
Методы адаптации представляют собой достаточно общий итеративный процесс решения задач стохастического программирования — процесс совершенствования решающих правил или статистических характеристик решающих распределений — по последовательным реализациям наборов случайных параметров условий задач. Формальная основа методов адаптации — различные обобщения схемы стохастической аппроксимации. [c.15]
В [147] получены условия оптимальности для задач вида (3.7) — (3.9). Они позволяют построить методы вычисления апостериорных решающих распределений для стохастических задач достаточно общего вида. При заданном распределении ш решающие распределения могут быть построены с помощью методов, обобщающих методы возможных направлений. В случаях, когда можно наблюдать реализацию со, для построения апостериорных решающих распределений предлагаются итеративные вычислительные схемы, обобщающие методы стохастической аппроксимации. [c.141]
В (148] и 306] условия оптимальности решения стохастических задач с фиксированным функциональным видом априорных решающих распределений использованы для построения адаптивных алгоритмов вычисления набора а искомых параметров распределения. При некоторых предположениях можно доказать, что такие итеративные алгоритмы, основанные на идеях стохастической аппроксимации, позволяют по последовательным реализациям случайных параметров условий задачи получить последовательность векторов ап, сходящуюся к оптимальному [c.144]
Эмпирическая функция распределения (рис. 6.3.9) имеет ступенчатую форму и может быть сглажена непрерывной функцией для удобства моделирования. Для аппроксимации могут быть применены полиномиальная, экспоненциальная или -образные функции, а также их вариации в кусочной форме. В некоторых случаях для аппроксимации применяют сплайн-функции порядка k, например, кубический сплайн ( = 3). [c.318]
Дисперсия распределения Пуассона равна математическому ожиданию, поэтому можно приблизить распределение Пуассона (X) к нормальному распределению с параметрами (X, X) при условии, что значение X достаточно велико. Однако надо отметить, что нормальное распределение — это непрерывное распределение, тогда как распределение Пуассона — дискретное. Таким образом, требуется поправка на непрерывность при аппроксимации. [c.207]
И наконец, следует уточнить, в соответствии с каким именно критерием качества аппроксимации неизвестных величин среднедушевых семейных денежных сбережений у (к) и уср (x) с помощью функции В0 + BI мы будем определять наилучший способ прогноза ср (х) по х. Наиболее обоснованное и точное решение этого вопроса опирается на знание вероятностной природы (а именно типа закона распределения вероятностей) остатков е в модели (В.З). Так, например, известно [14, с. 281], что если предположить, что при любых значениях к распределение вероятностей остатков е описывается (0, а2)-нормальным законом (т. е. нормальным законом со средним значением, равным нулю, и с некоторой, вообще говоря, неизвестной, но постоянной, т. е. не зависящей от х дисперсией а2) и что остатки е (дсг-), i = 1, 2,. .., п, характеризующие различные наблюдения, статистически независимы, то наименьшая ошибка прогноза (/ср (х) с помощью модели / (х) F (т. е. функция / (х) подбирается из класса F) обеспечивается требованием метода наименьших квадратов [c.17]
При другой статистической природе остатков е или при отсутствии достаточной информации о типе их вероятностного распределения возможен иной, чем по (В. 7), выбор критерия качества аппроксимации Ап (см. гл. 7). Отметим, однако, что наиболее широкое распространение в статистической практике именно критерия наименьших квадратов (В. 7) подкреплено рядом исследований [15, 196]. В них обосновываются хорошие прогностические свойства моделей, полученных в соответствии с (В. 7) и в ситуациях, характеризующихся различными отклонениями от нормальности и взаимной независимости остатков е (л ). [c.19]
В общем случае для точного описания функции регрессии необходимо точное знание условного закона распределения результирующего показателя г (при условии, что = X). Поскольку в статистической практике мы никогда не располагаем такой информацией, то обычно ограничиваются поиском подходящих аппроксимаций для / (X), основанных на исходных статистических данных вида (В.1) (о методах построения таких аппроксимаций см. гл. 7 — 10). [c.166]
В предыдущем параграфе обращается внимание читателя на то, что в статистической практике приходится ограничиваться поиском подходящих аппроксимаций для неизвестной истинной функции регрессии / (X), поскольку исследователь не располагает точным знанием условного закона распределения вероятностей анализируемого результирующего показателя г (при условии, что объясняющие переменные приняли значение , равное X). [c.167]
Для точного описания функции регрессии / (X) = Е (л 15= = X) необходимо знание закона условного распределения результирующего показателя т] (при условии = X). В статистической практике ограничиваются оценкой (на основании имеющихся выборочных данных вида (В.1)) подходящих аппроксимаций fa (X) фуНКЦИИ / (X). [c.173]
Для оценки финансовых активов существует множество моделей. Как правило, их целью является определение реальной цены котируемых финансовых инструментов, например облигаций, либо оценка рискованности портфеля активов с помощью прогнозирования. Эти модели позволяют выработать политику управления рисками и определить коэффициенты хеджирования. Зачастую определение коэффициентов хеджирования является их основной целью, еще более важной, чем теоретическая оценка самих активов. Существует два основных подхода к моделированию структуры процентных ставок и ее динамики параметрический и непараметрический. В данной главе нами будет рассмотрен непараметрический подход, не требующий принятия никакой априорной гипотезы относительно вида функционала процесса, формирующего структуру процентных ставок, а также вида распределения, характеризующего динамику наблюдаемых случайных величин. На примере исторического набора данных Эрик де Бодт, Филипп Грегори и Мари Коттрелл используют алгоритм СОК для аппроксимации распределения структуры процентных ставок и ее изменения с течением времени (структурных потрясений). Производимое на этой основе численное моделирование методом Монте-Карло позволяет получить картину долгосрочного развития структуры процентных ставок в течение пяти лет. [c.63]
Такого рода характеристика явлений, влияющих на уровень и динамику валютного курса, является непременным этапом, предшествующим самостоятельному статистическому анализу факторов на основе конкретного цифрового материала. Дальнейший анализ выглядит чаще как моделирование взаимосвязей и оценка тесноты взаимозависимости (корреляционно-регрессионный анализ). Напомним, что выбор функции осуществляется исходя из показателей значимости уравнения и ошибок аппроксимации. Это относительная ошибка аппроксимации, средняя квадратическая ошибка аппроксимации (6ОСТ) (чем они меньше, тем лучше уравнение) и коэффициент множественной детерминации (R2) или коэффициент множественной корреляции (R) (чем ближе он к 1, тем более вероятность, что уравнение регрессии носит совершенно случайный характер). Для проверки значимости используют F-критерий с распределением Фишера. [c.670]
Для точного описания уравнения регрессии необходимо знать условный закон распределения зависимой переменной Y при условии, что переменная X примет значение дс, т. е. Х=х. В статистической практике такую информацию получить, как правило, не удается, так как обычно исследователь располагает лишь выборкой пар значений (х/, у,) ограниченного объема п. В этом случае речь может идти об оценке (приближенном выражении, аппроксимаций) по выборке функции регрессии. Такой оценкой1 является выборочная линия (кривая) регрессии [c.52]
Ситуация меняется при переходе к логарифмам отношения цен, то есть к величине Ayk = ln(/ I Pk i). Распределение логарифмов уже может быть симметрично и возможна его аппроксимация одним из аналитических законов распределения, которые были рассмотрены во второй главе (как правило обобщенным экспоненциальным распределением). При этом логарифм цены в произвольный момент времени складывается из логарифма цены в начальный момент времени (эта величина пред [c.139]
Эта аппроксимация проходит только в случае биномиального распределения (т. е. при двух сценариях в спектре). Чем более уклоняются вероятности от 0,5 на сценарий, тем менее точной она становится. Другими словами, это решение является точным, когда вы дихотомизируете два сценарных спектра в противном случае она превращается в аппроксимацию убывающей точности. [c.147]
Сходные ошибки можно найти и в других трех квадрантах. Такой неточностью мы обязаны тому, что дихотомизировали исходное распределение слишком далеко от действительно равновероятного уровня (мы дихотомизировали на уровнях 0,74074 и 0,777). Поэтому наши аппроксимации совместных распределений оказались менее точными. [c.151]
Обучение PN-сети складывается из двух процессов адаптации. На первом этапе весовые векторы слоя Кохонена настраиваются так, чтобы моделировать распределение входных векторов. Очевидно, что этот процесс является процессом самостоятельной адаптации. При этом точность аппроксимации будет гарантирована только тогда, когда набор обучающих примеров будет статистически представительным (репрезентативным) для области, на которой действует отображение. Второй адаптационный процесс является несамостоятельным. Он начинается после того, как произошло обучение слоя Кохонена. Происходит настройка весов выходного слоя Гроссберга на примерах с заданным выходом. При этом настраиваются только [c.40]
Работа Бунке [45] дает основания для различных обобщений стохастической аппроксимации. В [45] приведена общая схема построения случайной последовательности, сходящейся к данному числу. Используя частные варианты этой схемы, удается получить случайные последовательности, аппроксимирующие медиану функции распределения, корень уравнения f(x)=a, максимум функции f(x), где f(x)- — однозначно определяемая медиана случайной величины у (со, х). [c.351]
В [51] доказано утверждение, аналогичное теореме 6.1, для алгоритма стохастической аппроксимации глобального экстремума многоэкстремального математического ожидания случайного функционала на сепарабельном гильбертовом пространстве. Специфика бесконечно-мерного пространства учитывается тем, что условие (6.2), которому нельзя удовлетворить в бесконечно-мерном случае, заменяется следующим ограничением на функцию распределения случайного вектора цп [c.372]
Замечание 1. Получение результата измерения служит промежуточным этапом, ка котором измерительная информация должна представляться я форме, удобной для ее дальнейшей обработки (переработки). Такой формой является представление результата измерения с помощью числовых характеристик закона распределения, вероятности, При однократном измерении чаще всего используется такая числовая характеристика законов распределения вероятности, как среднее квадратичегкое отклонение i лли его аналог). С ее помощью определяются пределы, в которых на-ходк ск знг-ение измеряемой величины, осуществляется внесение поправки, очное значение которой неизвестно. Если пользоваться стандартными аппроксимациями законов распределения вероятности, представленными в табл. 8. то переход к этой числовой характеристике удобно осуществлять с помощью коэффициентов, приведенных в третьей графе. [c.89]
Смотреть страницы где упоминается термин Аппроксимация распределений
: [c.42] [c.67] [c.67] [c.46] [c.119] [c.238] [c.174] [c.191] [c.51] [c.46] [c.42]Смотреть главы в:
Теория очередей и управление запасами -> Аппроксимация распределений
