Теоретических оценок нормальной аппроксимации нет. Однако накопленный опыт вычислений (относительно небольшой) подтверждает целесообразность использования этого приближенного способа вычисления функции (L ). [c.299]
Должно быть при этом понятно, что слова "в первом приближении" связаны с тем, что на самом деле величины hk не являются, вообще говоря, нормально распределенными, и вопрос о том, насколько истинные уровни надежности приведенных выше доверительных интервалов отличаются от 68 % и 90 %, требует дополнительного исследования относительно точности нормальной аппроксимации. [c.197]
| Рис. 6.2. Интегральная зависимость вероятность — ущерб и ее аппроксимация нормальной функцией распределения | 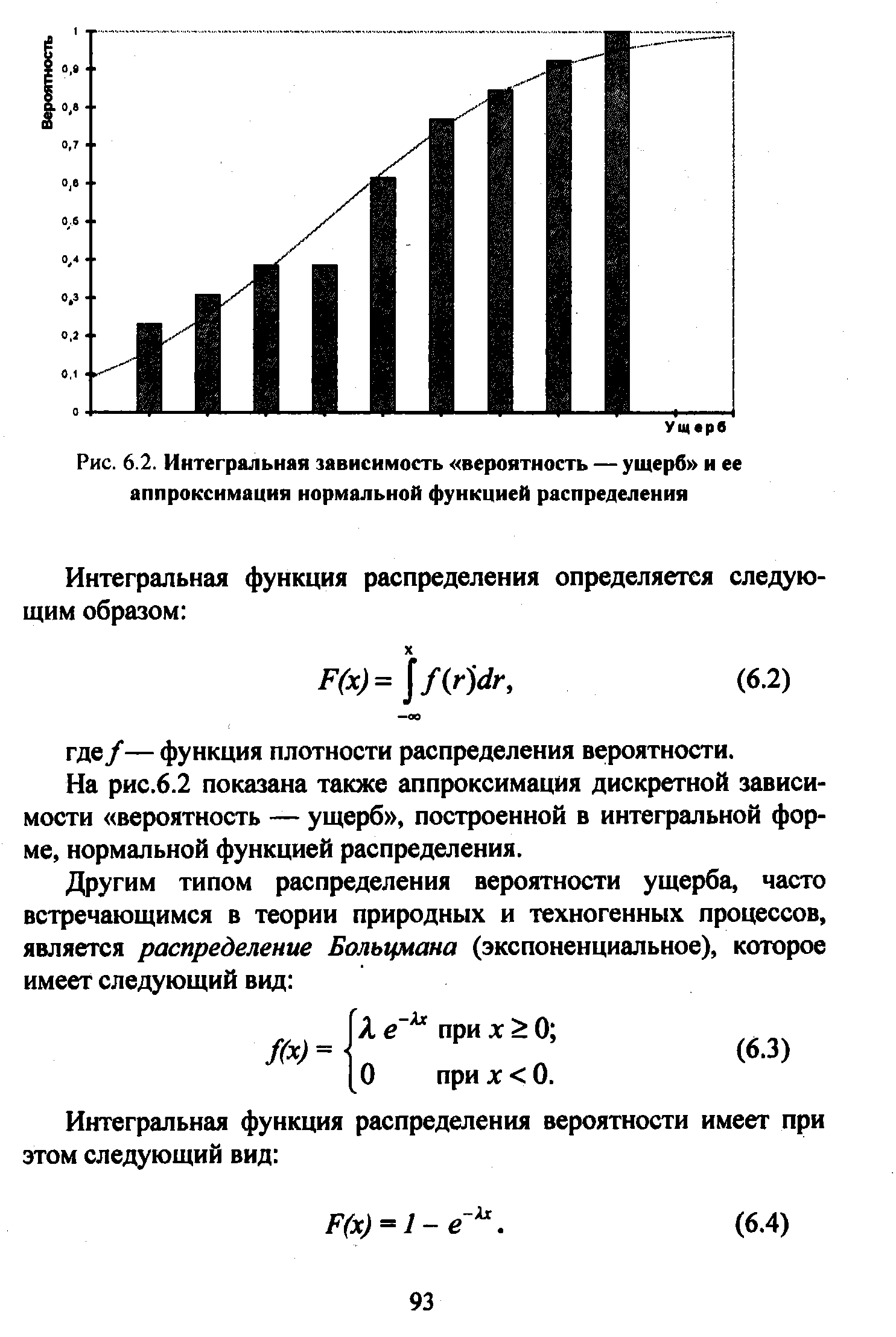 |
Пример 5. Предположим, что спрос в примере 1 в действительности представляет собой аппроксимацию случайной ситуации, при которой ежедневный спрос распределен нормально со средним ц= 100 и [c.556]
Одно из основных требований метода наименьших квадратов состоит в том, чтобы функция была линейной относительно оцениваемых параметров. В конечном счете соблюдение этого требования допускает такие функциональные преобразования исходных данных, при которых система нормальных уравнений (см. стр. 65) остается линейной относительно искомых параметров при данном функционале, описывающем точность аппроксимации. [c.46]
Дисперсия распределения Пуассона равна математическому ожиданию, поэтому можно приблизить распределение Пуассона (X) к нормальному распределению с параметрами (X, X) при условии, что значение X достаточно велико. Однако надо отметить, что нормальное распределение — это непрерывное распределение, тогда как распределение Пуассона — дискретное. Таким образом, требуется поправка на непрерывность при аппроксимации. [c.207]
И наконец, следует уточнить, в соответствии с каким именно критерием качества аппроксимации неизвестных величин среднедушевых семейных денежных сбережений у (к) и уср (x) с помощью функции В0 + BI мы будем определять наилучший способ прогноза ср (х) по х. Наиболее обоснованное и точное решение этого вопроса опирается на знание вероятностной природы (а именно типа закона распределения вероятностей) остатков е в модели (В.З). Так, например, известно [14, с. 281], что если предположить, что при любых значениях к распределение вероятностей остатков е описывается (0, а2)-нормальным законом (т. е. нормальным законом со средним значением, равным нулю, и с некоторой, вообще говоря, неизвестной, но постоянной, т. е. не зависящей от х дисперсией а2) и что остатки е (дсг-), i = 1, 2,. .., п, характеризующие различные наблюдения, статистически независимы, то наименьшая ошибка прогноза (/ср (х) с помощью модели / (х) F (т. е. функция / (х) подбирается из класса F) обеспечивается требованием метода наименьших квадратов [c.17]
При другой статистической природе остатков е или при отсутствии достаточной информации о типе их вероятностного распределения возможен иной, чем по (В. 7), выбор критерия качества аппроксимации Ап (см. гл. 7). Отметим, однако, что наиболее широкое распространение в статистической практике именно критерия наименьших квадратов (В. 7) подкреплено рядом исследований [15, 196]. В них обосновываются хорошие прогностические свойства моделей, полученных в соответствии с (В. 7) и в ситуациях, характеризующихся различными отклонениями от нормальности и взаимной независимости остатков е (л ). [c.19]
Дункан [89] распространил свою модель [88] для одной причины разладки на случай нескольких ее причин. Каждая причина разладки обусловливает смещение среднего параметра процесса на определенную величину. Каждая причина разладки создает смещение среднего параметра процесса определенной величины. Времена, предшествующие разладке, предполагаются независимыми экспоненциально распределенными величинами. Разработаны и рассмотрены две модели. Модель I предполагает, что разладка происходит один раз и ее состояние длится до тех пор, пока она не будет обнаружена в течение всего этого времени другие причины разладки не влияют на процесс. Модель II допускает после первой разладки вторую, вызванную другой причиной. Дункан использовал метод прямого исследования, чтобы определить локальный минимум функции затрат для различных стоимостных параметров и трех выбранных распределений (имеющих приблизительно одинаковые характеристики) а именно экспоненциального, равномерного и на половину нормального. Численные результаты показали, что в случае нескольких причин разладки влияние изменения стоимостных параметров на оптимальные параметры контрольных карт аналогично тому, которое имеет место при одной причине разладки. Дункану удалось показать, что при наличии нескольких причин разладки получается ситуация, в которой аппроксимация достигается более обоснованно [88]. [c.135]
В исследовательской практике аппроксимации используют для аналитического описания поверхностей, изображенных на картах, и выполнения с ними различных действий суммирования, вычитания, интегрирования и дифференцирования для подсчета объемов тел, ограниченных этими поверхностями для решения множества других задач. Одно из направлений использования аппроксимаций - это разложение поверхностей на составляющие, что позволяет выделять и анализировать нормальные и аномальные факторы развития и пространственного размещения явлений. [c.221]
Центральная предельная теорема в какой-то степени оправдывает столь частое использование в экономике нормального закона распределения для аппроксимации функций распределения случайных величин, предположительно являющихся суммой большого количества независимых случайных величин. [c.110]
Если модель адекватна данным, ошибки являются белым шумом, и при больших значениях п и k величина г имеет распределение, близкое к нормальному N(0, ). Причем на практике хорошая аппроксимация начинается с k = 5 -г 6. Поэтому значение г вне интервала 0 -4= позволяет на 5%-ном уровне значимости отвергнуть гипотезу равенства нулю коэффициента корреляции р . [c.306]
Последняя аппроксимация тем точнее, чем меньше o t по сравнению с F(t). Логнормальное распределение, в отличие от нормального, несимметрично и целиком лежит в положительной области. Чем меньше (T t по сравнению с F(t), тем ближе логнормальное распределение к нормальному со средним [c.21]
Неоднородность дисперсий. Рассмотрим влияние дисперсий на вероятность того, что наблюдаемое значение из некоторой худшей совокупности больше, чем наблюдаемое значение из наилучшей совокупности. Если мы используем аппроксимацию с помощью нормального распределения для k распределений, то эта вероятность определится следующим образом [c.275]
Математики затратили много времени, чтобы определить реальное распределение движений цен акций. Относительно реального распределения есть некоторые разногласия. Тем не менее логарифмически нормальное распределение, как правило, принимается в качестве разумной аппроксимации движения цен. Речь идет не только о ценах на акции. Это могут быть цены фьючерсов, цены индексов или процентные ставки. [c.341]
Таким образом, используя для аппроксимации G(x) функцию нормального распределения, мы приходим к модели [c.16]
При сопоставлении уравнений (3.1) и (3.5) можно видеть, что скорость, требуемая для поправки за нормальное приращение в горизонтально-слоистой среде, равна среднеквадратичной скорости, при условии, что выполнена аппроксимация короткой расстановкой. [c.8]
После аппроксимации короткой расстановкой и малым наклоном нормальное приращение является гиперболическим для всех случаев [c.13]
На рис.2 представлены распределение этой же статистики при дискретности наблюдений 1 день, и аппроксимация его нормальным распределением и гипергеометрическим. Как легко заметить, эмпирическое распределение в первом случае совпадает с нормальным, но с введением дискретности и увеличением интервала наблюдения качество аппроксимации нормальным распределением ухудшается. Для улучшения аппроксимации было разработано и продолжает разрабатываться большое число моделей. Проводимые нами исследования эволюции финансовых индексов показали, что в качестве базовой модели удобно использовать гиперболическое распределение [2J, плотность которого описывается уравнением [c.135]
Объем выборки для сравнения двух биномиальных вероятностей можно определить с помощью нормальной аппроксимации. В [А1-Bayyati, 1971] дается описание другого способа решения этой задачи, но предлагаемая процедура консервативна и, следовательно, менее привлекательна в случае дорогостоящих имитационных экспериментов. Рассмотрим подробнее общую проблему проверки гипотез (в противоположность оцениванию). [c.150]
Указание. Функция lsolve(A, b) возвращает вектор х решения системы Ax = b, найденного методом Гаусса с оценкой числа обусловленности. Здесь не используется явная формула решения нормальной обобщенной системы х = (АТА)" АТЬ, поскольку часто в задачах об аппроксимации эмпирических данных [c.89]
Работы (Шевяков А.Ю., Кирута А.Я., 1999 Ершов Э.Б., Майер В.Ф., 1998 Суворов А.В., Ульянова Е.А., 1997 Айвазян С.А., 1997) содержат различные доводы, подтверждающие справедливость наших критических замечаний (i) - (iv) (см. выше). В работе (Великанова Т. и др., 1996) описан подход, также основанный на модели смеси лог-нормальных распределений однако он не оснащен необходимым инструментарием, позволяющим проводить грамотный эконометри-ческий анализ этой смеси, и не предлагает никаких способов учета скрытых от прямого наблюдения данных. Описанный в (Ершов Э.Б., Майер В.Ф., 1998) подход, опирающийся на полиномиальную аппроксимацию плотности анализируемого закона распределения, слишком формален и не позволяет построить феноменологическую модель изучаемого явления, дать содержательную интерпретацию параметрам модели, учесть ненаблюдаемый спектр расходов. [c.14]
В этом параграфе мы дадим обзор тех существующих ММР, которые, по нашему мнению, могут пригодиться в имитационных экспериментах. Поскольку наша главная забота—применимость в моделировании, будем классифицировать методы по предпосылкам, лежащим в их основе. Все методы предполагают независимость наблюдений (внутри и между совокупностями). Из параметрических методов возьмем только ММР для нормальных распределений. Мы предполагаем, что этот тип методов наиболее широко применим в имитационном моделировании по сравнению с другими параметрическими методами. Нормальное распределение служит адекватной аппроксимацией многих других распределений, и отклонения между действительным неизвестным распределением и нормальным предполагаются не столь уж страшными. Мы вернемся к проблеме робастности методов в следующем параграфе. Методы, основанные на других распределениях, кратко описаны в V.B.5. Здесь же мы изучим еще непараметрические или полунепараметрические ММР. Помимо различий параметрические—непараметрические между распределениями могут существовать и другие различия только в расположении или как в расположении, так и в форме. Для нормальных совокупностей последнее различие эквивалентно различию равные дисперсии — неравные дисперсии. Другая классификация известные дисперсии — неизвестные дисперсии. Все ММР из этого параграфа используют подход, основанный [c.221]
Комплексные сценарии, включающие в себя изменения волатильностей и корреляций, используются при стресс-тестировании показателя VaR (stressing VaR), которое иногда выделяют в самостоятельную разновидность стресс-тестирования. Согласно распространенным рекомендациям, при расчете VaR ковариационным методом или методом Монте-Карло стресс-тестирование следует проводить, варьируя в различных комбинациях входные параметры — волатильности и корреляции. Однако не следует забывать, что дельта-нормальный метод расчета VaR основан на линейной аппроксимации чувствительности цен инструментов к относительно небольшим (в пределе — к бесконечно малым) изменениям факторов риска . Для инструментов с нелинейными функциями ценообразования погрешность такого приближения будет тем больше, чем сильнее реальное изменение фактора риска отличается от того, которое предполагалось при оценке чувствительности. В случае стресс-тестирования речь идет именно о внезапных и очень больших по величине скачках факторов риска, поэтому необходимо либо специально оценивать линейную чувствительность к изменениям такого масштаба, либо проводить стресс-тестирование только корреляционной, а не ковариационной матрицы. [c.595]
Для одного горизонтального слоя с постоянной скоростью кривая времен пробега в функции выноса представляет собой гиперболу (Раздел 3.2). Разность времен пробега при данном выносе и при нулевом выносе называется нормальным приращением. Скорость, необходимая для ввода поправки за нормальное приращение, скоростью нормального приращения (NMO velo ity).Для одной горизонтальной отражающей поверхности скорость нормального приращения равна скорости в среде над отражающей поверхностью (ОН). Для наклонной ОН эта скорость равна скорости в среде, деленной на косинус угла наклона. При наблюдении наклонной ОП в трех измерениях дополнительным фактором становится азимут (угол между направлением падения и направлением профиля). Зависимость времени пробега от выноса для последовательности плоских горизонтальных слоев с постоянной скоростью аппроксимируется гиперболой. При меньших высотах эта аппроксимация лучше, чем при больших выносах. Для малых выносов скорость нормального приращения для горизонтально-слоистого разреза среднеквадратичной скорости до границы рассматриваемого слоя. В среде, состоящей из слоев с произвольными наклонами уравнение времени пробега усложняется. Однако, на практике, если наклоны незначительные, а длина расстановки меньше глубины отражающей поверхности, можно считать, что время пробега аппроксимируется гиперболой. Для границ слов, формы которых произвольны, это допущение не действительно. [c.2]
Эти уравнения можно решить для остаточной статики, ассоциированной с положениями источников NS, положениями сейсмоприемников NR, структурными элементами NG и элементами остаточного приращения NG. В обработке сейсмических данных количество этих элементов может быть довольно большим. Задача с двумя параметрами, заданными уравнением (3.34), решается просто. Однако, когда мы имеем дело с большим количеством линейных уравнений, необходимо быстрое и точное решение. Для решения уравнения (3.35) Wiggins и др. (1976) воспользовался итеративной процедурой Гаусса-Зайделя (Gauss-Saidel). Эту процедуру лучше всего представить, если вернуться к предыдущему примеру, линейной аппроксимации и решив уравнение (3.34) относительно а и Ъ. Если записать (3.34) в виде нормальных уравнений [c.57]
Качество модели оценивается двумя характеристиками, дополняющими друг друга точностью и адекватностью. На основе отдельных критериев точности и адекватности формируется обобщенный критерий — взвешенная сумма обобщенного критерия точности и обобщенного критерия адекватности. Веса этих слагаемых составляют соответственно 0,75 и 0,25. В качестве представителя характеристик точности используется нормированное значение средней относительной ошибки аппроксимации, среднеквадратического отклонения, коэффициента детерминации, максимального отклонения, среднего значения (должно быть близко к нулю), а в качестве представителя критериев адекватности — нормированное значение критерия Дарбина-Уотсона и характеристики нормального закона распределения.Числовое значение обобщенного критерия качества находится между 0 и 100 чем оно выше, тем модель адекватнее. Обобщенный критерий формируется в соответствии со схемой формирования интегрированных критериев как комбинация частных прогнозов [c.74]
Возрастание требований к эффективности систем управления влечет за собой повышение требований к точности и адекватности моделей управляемых объектов. При этом требования по точности предъявляются как к прямой, так и обратной модели, а сама модель в общем случае понимается как обобщенная модель по Эйкхоффу [1].Особенно остро эта задача встает при создании систем прямого цифрового управления нелинейными объектами. Поскольку реальные объекты обычно характеризуются нелинейной, сложной структурой, а также неполнотой математического описания и информации как о самом объекте так и сигналах и помехах, действующих на него, существуют два подхода к решению задачи идентификации. Первый подход связан с аппроксимацией объекта набором (цепочкой) элементарных звеньев известной структуры, а построение модели сводится к оценке характеристик этих звеньев по данным нормальной эксплуатации. Сущность второго подхода состоит в желании ослабить зависимость результата решения задачи идентификации от ограничений, накладываемых априорными предположениями, и создании более общего унифицированного подхода к решению задачи идентификации. Примерами такого подхода являются разработки методов статистической линеаризации [2,3], метода функциональных преобразований [4,5] и информационных методов идентификации [6,7]. [c.96]
Смотреть страницы где упоминается термин Нормальная аппроксимация
: [c.149] [c.326] [c.174] [c.92] [c.46] [c.394] [c.121] [c.100] [c.190] [c.47] [c.176] [c.249] [c.565]Смотреть главы в:
Теория очередей и управление запасами -> Нормальная аппроксимация
