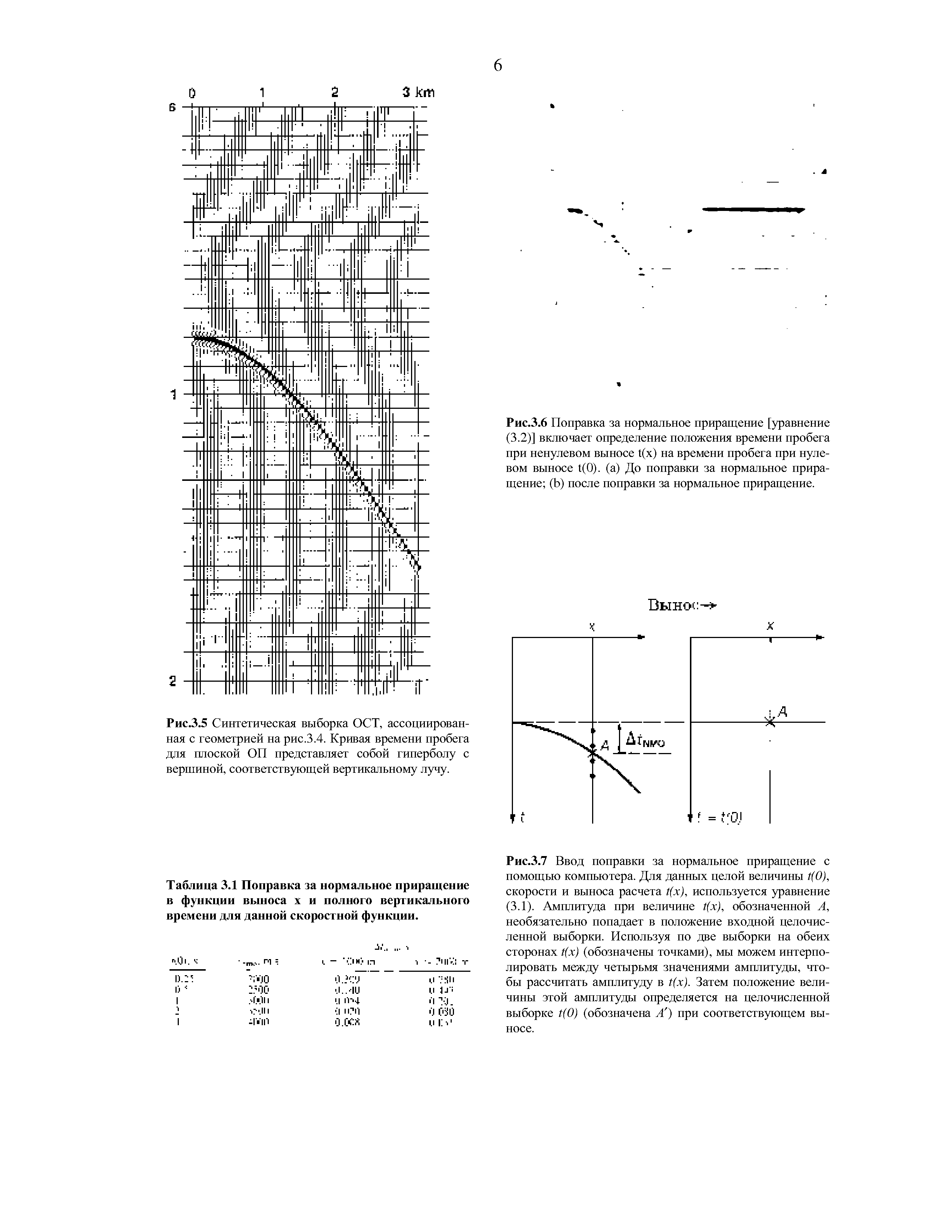
| Рис.2.19. Типичное распределение выносов Рис.2.20. Сейсмограмма ОПВ, исправленная за (двух- и трехмерные данные). нормальное приращение. |  |
Выбранные записи ОПВ, до или после поправки за нормальное приращение [c.196]
В основе общепринятого скоростного анализа находится предположение о гиперболичности годографа. В Разделе 3.3 рассмотрены различные подходы к скоростному анализу. Уравнение времени пробега является линейным в плоскости (t, х ). Вертикальное время и скорость суммирования для данной ОП можно оценить по линии, которая наилучшим образом аппроксимирует точки времени пробега, построенные на плоскости (t, х ). Другой способ оценки скорости ОГТ - это применение различных поправок за нормальное приращение к выборке ОСТ с использованием диапазона постоянных скоростей с последующим отображением их в ряд. Скорость, которая наилучшим образом сглаживает каждое отражение в функции выноса, выбирается как его скорость ОГТ. С другой стороны, можно суммировать небольшой участок профиля, используя ряд постоянных скоростей. Затем эти суммы постоянных скоростей можно построить в виде панели, называемой панелью VS. Скорости суммирования, которые дают желательную сумму, можно затем выбрать из панели. [c.3]
В горизонтально-слоистой среде годограф отраженных волн не всегда являются гиперболическими. Одной из причин отклонения времени пробега от совершенной амплитуды является присутствие статических сдвигов, обусловленных приповерхностными изменениями скорости. Статика может сильно исказить гиперболу, если имеют место значительные изменения рельефа поверхности земли или при изменении Змс в горизонтальном направлении. Остаточная статика часто сохраняется в данных даже после ввода начальных поправок за оцененные изменения Змс и отметок превышения (т.е. за полевую статику - см. Раздел 3.6). Следовательно, перед суммированием необходимо рассчитать поправки за эту остаточную статику и применить к выборкам ОСТ. Оценка выполняется после предварительного ввода поправки за нормальное приращение с использованием региональной скоростной функции или информации, полученной из последовательности предварительных скоростных анализов по профилю. После коррекции остаточной статики скоростные анализы обычно повторяются с целью улучшения селекции волн по скорости для суммирования, различные аспекты коррекции остаточной статики рассмотрены в Разделах 3.4.и 3.5. [c.4]
После того, как оценена скорость ОРТ, можно исправить времена пробега с целью устранения влияния выноса (рис.3.6). Затем трассы, исправленные за нормальное приращение, суммируются с целью получения суммарной трассы в положении данной ОСТ. [c.5]
Поправка за нормальное приращение определяется разностью между t(x) и t(0) [c.5]
| Таблица 3.1 Поправка за нормальное приращение в функции выноса х и полного вертикального времени для данной скоростной функции. | 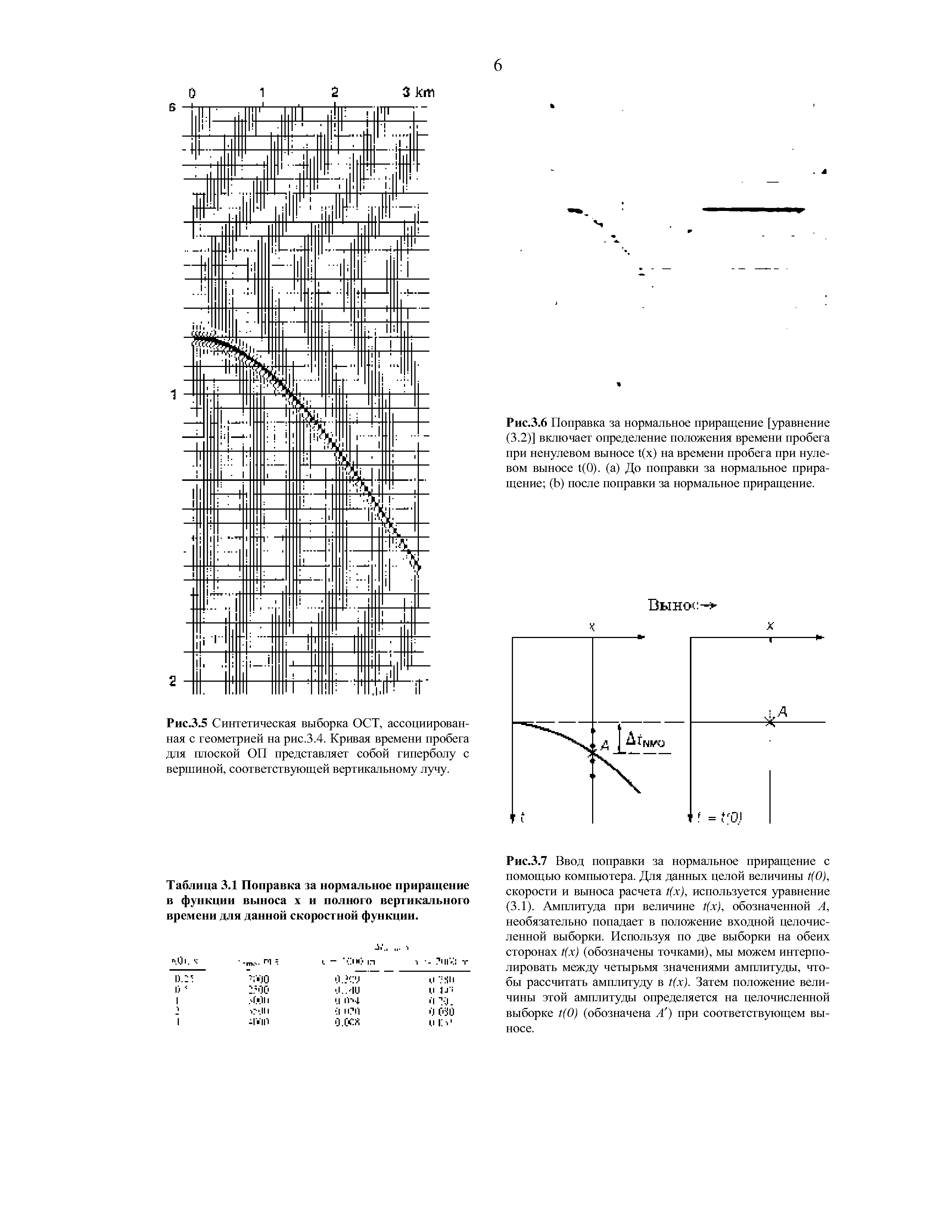 |
[c.7]
Нормальное приращение в горизонтально-слоистой среде [c.8]
При сопоставлении уравнений (3.1) и (3.5) можно видеть, что скорость, требуемая для поправки за нормальное приращение в горизонтально-слоистой среде, равна среднеквадратичной скорости, при условии, что выполнена аппроксимация короткой расстановкой. [c.8]
| Рис.3.9 Нормальное приращение для горизонтально-слоистой модели разреза [геометрия для уравнения (3.3)]. | ![Рис.3.9 Нормальное приращение для горизонтально-слоистой модели разреза [геометрия для уравнения (3.3)].](/pic1/118093251190143094221152184024190067018188098153.png) |
На рис.3.12Ь показана выборка ОСТ на рис.3.10а после поправки за нормальное приращение, которая рассчитывалась по уравнению (3.5) с использованием функции среднеквадратичной скорости, показанной на рис.3.11. В результате поправки за нормальное приращение возникает частотное искажение, в частности для неглубоких отражений и при больших выносах. Это называется растяжением нормального приращения и показано на рис.3.13. Форма волны с видимым периодом Г растягивается так, что ее период Т после ввода поправки за нормальное приращение становится больше, чем Т. Растяжение представляет собой частотное искажение, при котором сигналы смещаются в сторону низких частот. Растяжение можно представить как [c.9]
Рис.3.10 (а) Синтетическая выборка ОСТ, полученная по скоростной функции, показанной на рис.3.11 (Ь), (с), (d) -выборки ОСТ, полученные по среднеквадратичным скоростям (показаны под каждой выборкой), ассоциированным со второй, третьей и четвертой сверху отражающими поверхностями. Времена в (а) были выведены с применением интегральных уравнений луча для горизонтально-слоистого разреза. Таблица 3.2 Растяжение нормального приращения. g таблице 3 2 перечислены [c.9]
Вследствие растяжения формы волн на больших выносах суммирование выборок ОСТ, исправленных за нормальное приращение (рис.3.12Ь) будет сильно искажать неглубокие отражения. Эту проблему можно решить, обнуляя растянутые зоны в выборке. Автоматическое обнуление выполняется путем использования количественного определения растяжения, данного в уравнении (3.6). На рис.3.12с и d показаны две версии выборки ОСТ после ввода поправок за нормальное при- [c.10]
Рис.3.12 (а) Та же выборка, что на рис.3. Юа, (Ь) после поправки за нормальное приращение с применением функции среднеквадратичной скорости, показанной на рис.3.11 (с) и (d) после обнуления, использующего пробелы растяжения 50 и 100% соответственно. [c.10]
Другой метод оптимального выбора зоны обнуления - это постепенное суммирование данных. На рис.3.15а показана выборка ОСТ, исправленная за нормальное приращение без обнуления. На рис.3.15Ь показаны суммарные трассы, полученные по выборке ОСТ (рис.3.15а), где крайняя правая трасса -такая же, как во входной выборке ОСТ. Вторая справа трасса - сумма двух трасс на ближнем выносе и т.д. (кратность суммирования постепенно повышается). Крайняя левая трасса представляет собой сумму с полной кратностью на входной выборке ОСТ. Следуя волновому фронту по определенному сигналу и наблюдая, где происходят изменения, можно по- [c.11]
| Рис.3.13 Сигнал (а) периодом Г растянут в сигнал (Ь) с периодом Т > Т после поправки за нормальное приращение. | 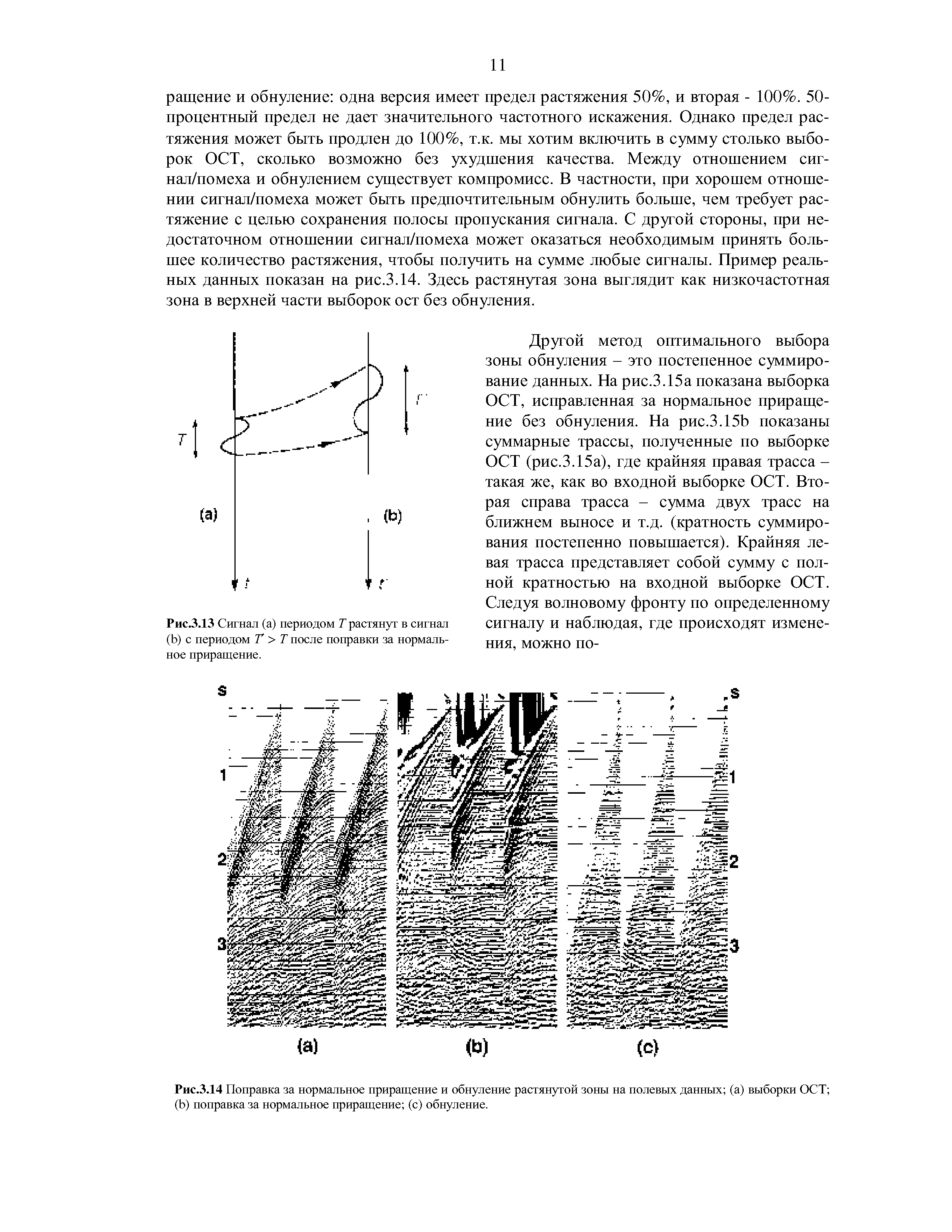 |
| Рис.3.14 Поправка за нормальное приращение и обнуление растянутой зоны на полевых данных (а) выборки ОСТ (Ь) поправка за нормальное приращение (с) обнуление. | 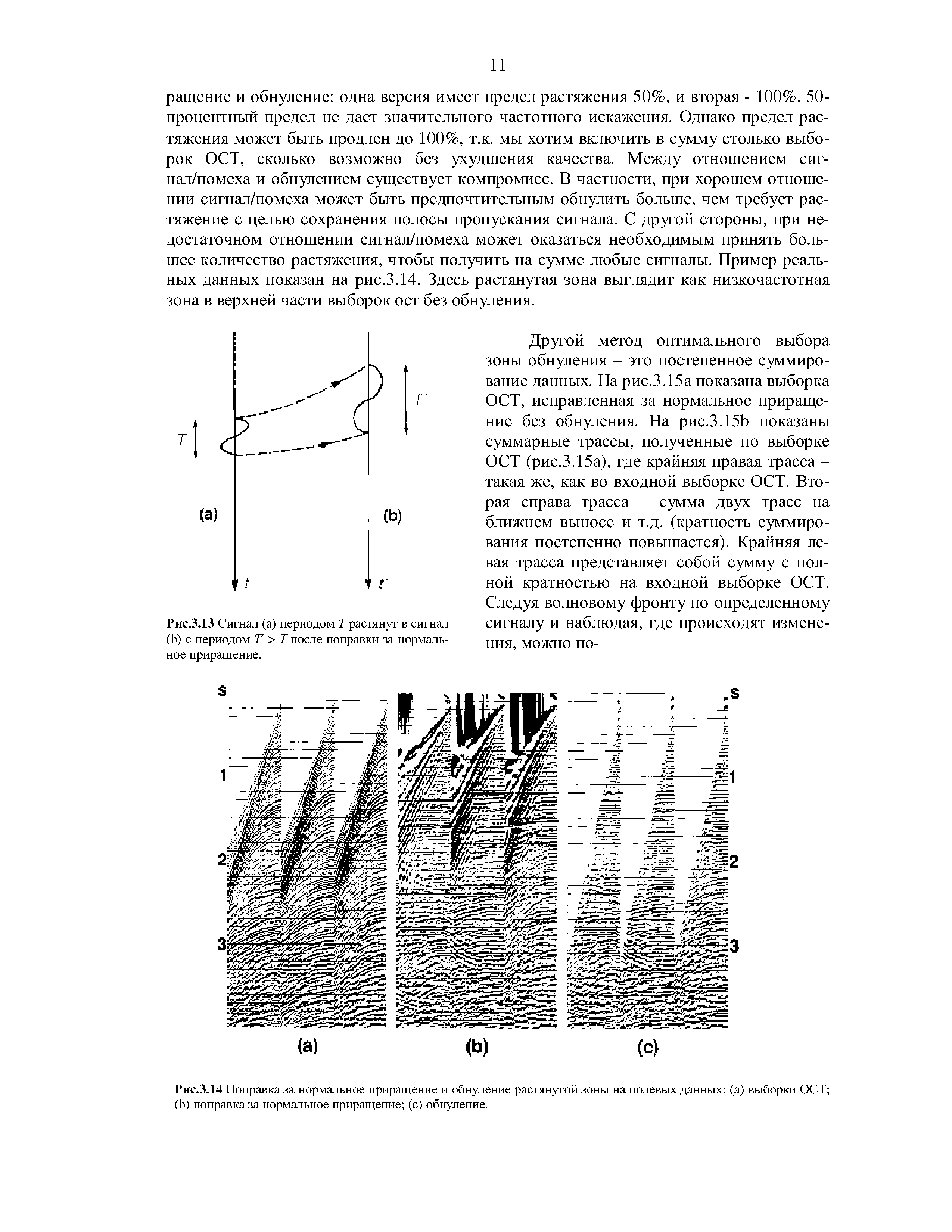 |
Растяжение нормального приращения определяется как частотное искажение, которое возникает из-за поправки за нормальное приращение. Пакеты программ могут моделировать растяжение в процентах в зависимости от времени на каждой трассе синтетических данных (Yilmaz, 1987, стр.160, ур. 3.6). Схема группы сейсмоприемников должна включать только те выносы, которые создают растяжение нормального приращения меньше требуемого (например, не более 20%) на времени полного пробега до объекта поиска [c.53]
Необязательно, чтобы трассы в средней зоне имели ближние выносы. Более отдаленные трассы содержат глубинные данные из-за обнуления нормального приращения, но эти данные мигрируются дальше в горизонтальном направлении. Если бины вблизи внешней границы второй зоны содержат только дальние трассы, а бины, ближайшие к внутренней зоне содержат более ближние трассы (следовательно, малоглубинные данные), хороший результат миграции на границе внутренней зоны (зоны изображения) должен сказаться на всех глубинах. [c.72]
Иногда для создания хорошего состава выносов используется супер-бин, т.е. несколько бинов, объединенных в группу. Все выносы должны быть сгруппированы по азимуту, поскольку скоростной анализ представляет собой свойство направленности в 3-D съемке. Каждый набор выносов в каждом диапазоне азимутов должен адекватным образом определять кривые нормального приращения это означает, что изменение А должно превышать одну длину волны (рис.10.2а). Супербин должен быть достаточно малым, чтобы не размывались геологические структуры (рис.10.2Ь). [c.197]
Разрешение по скорости каждого бина ОСТ в реальной съемке может быть рассчитано путем создания синтетической оси синфазности с определенной скоростью и временем, с последующим суммированием синтетических данных с различными скоростями. Пример такой синтетической оси синфазности для действительного состава выносов по нескольким ОСТ реальной 3-D съемки показан на рис.10.3. Несколько синтетических трасс выборки ОСТ до ввода поправки за нормальное приращение можно видеть на рис.10.За. Результат суммирования одной из этих выборок (трасс, принадлежащих одной ОСТ), представлен на рис.Ю.ЗЬ. Правильная скорость достаточно очевидна (приблизительно трасса 201 VS), но возможна небольшая ошибка в пикинге, особенно в реальных данных. [c.197]
| Рис.10.2. Концепции скоростного анализа для нормального приращения (а) и супербинов (Ь). |  |
| Рис.10.10. Перемещение данных в процессе ввода поправки за нормальное приращение, поправки за наклон и миграции (по Sheriff, 1991). | 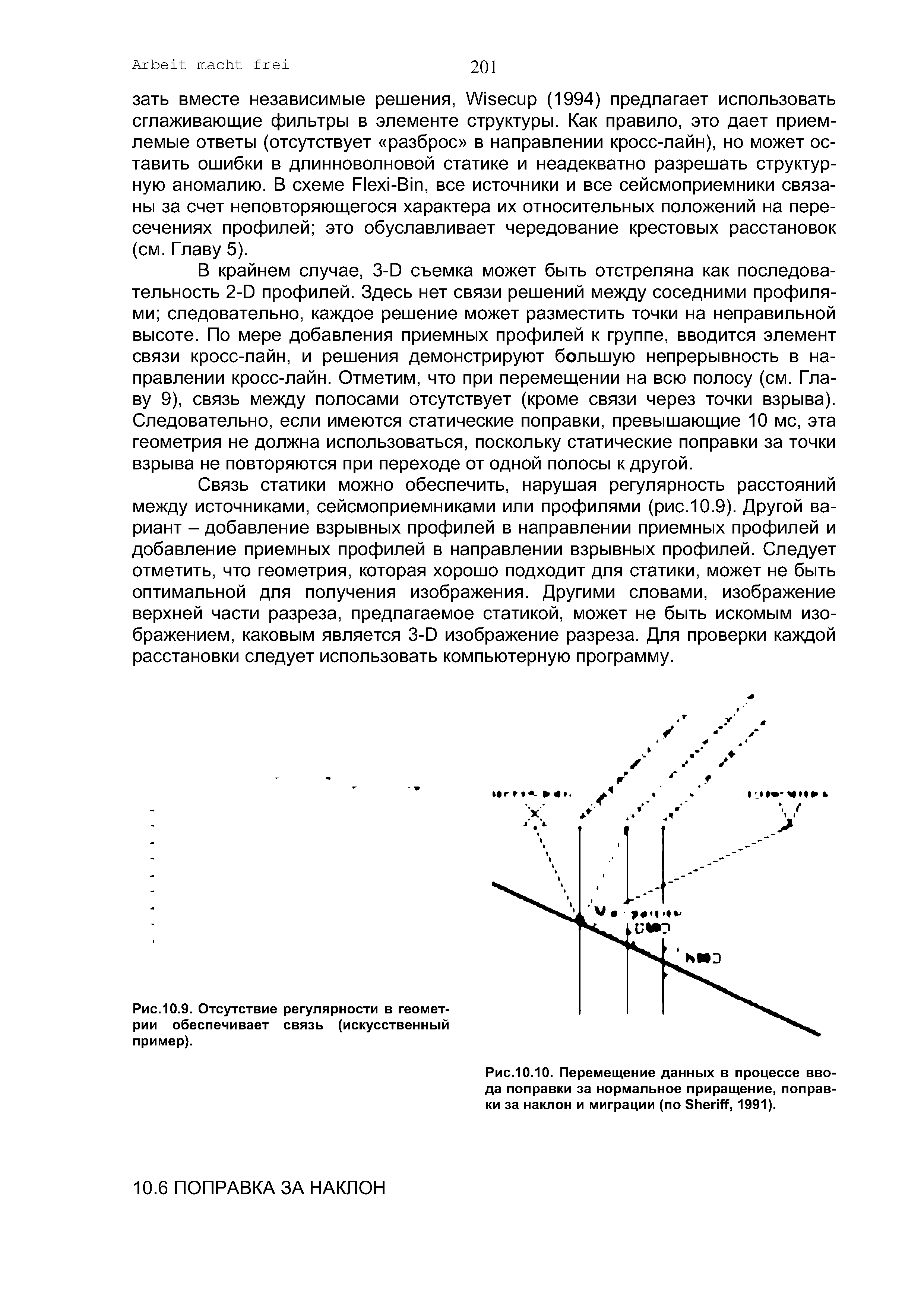 |
DMO представляет собой частный случай миграции перед суммированием, после которого следует поправка за нормальное приращение и суммирование. Hale (1984) обсуждает процесс в деталях. Чаще всего применяется DMO с постоянной скоростью. Описание DMO, изменяющейся во времени, имеется у Meinardus и S hlei her (1991). [c.202]
Предположим, что Н - вынос, V — средняя скорость, t - интересующее нас время. В таком случае, энергия на времени t в бине ОСТ получена от всех пар источник-сейсмоприемник, которые пересекают бин, и средние точки которых не отклоняются от центра бина больше, чем на H2+(2xVxt) (рис.10.11, Deregowski, 1982). Кратность и количество неповторяющихся выносов в каждом бине после ввода поправки за нормальное приращение на времени t являются хорошими мерами отклика DMO. Из рис.10.11 следует [c.202]
Для одного горизонтального слоя с постоянной скоростью кривая времен пробега в функции выноса представляет собой гиперболу (Раздел 3.2). Разность времен пробега при данном выносе и при нулевом выносе называется нормальным приращением. Скорость, необходимая для ввода поправки за нормальное приращение, скоростью нормального приращения (NMO velo ity).Для одной горизонтальной отражающей поверхности скорость нормального приращения равна скорости в среде над отражающей поверхностью (ОН). Для наклонной ОН эта скорость равна скорости в среде, деленной на косинус угла наклона. При наблюдении наклонной ОП в трех измерениях дополнительным фактором становится азимут (угол между направлением падения и направлением профиля). Зависимость времени пробега от выноса для последовательности плоских горизонтальных слоев с постоянной скоростью аппроксимируется гиперболой. При меньших высотах эта аппроксимация лучше, чем при больших выносах. Для малых выносов скорость нормального приращения для горизонтально-слоистого разреза среднеквадратичной скорости до границы рассматриваемого слоя. В среде, состоящей из слоев с произвольными наклонами уравнение времени пробега усложняется. Однако, на практике, если наклоны незначительные, а длина расстановки меньше глубины отражающей поверхности, можно считать, что время пробега аппроксимируется гиперболой. Для границ слов, формы которых произвольны, это допущение не действительно. [c.2]
Между скоростью нормального приращения (скоростью ОГТ) и скоростью суммирования существует различие, которое на практике часто игнорируется. Скорость ОГТ основывается на гиперболичности времени пробега при коротких расстановках (Тапег и Koehler, 1969 Al- halabi, 1973), а скорость суммирования исходит из гиперболы, которая наилучшим образом аппроксимирует данные по всей длине расстановки. Тем не менее, скорость суммирования и скорость ОГТ в общем случае рассматриваются как эквивалентные. [c.3]
Процедура ввода поправки за гиперболическое нормальное приращение показана на рис.3.7. Идея состоит в нахождении величины амплитуды в точке А на выборке, исправленной за нормальное приращение, по величине амплитуды в точке А на первоначальной выборке ОСТ. При данных t(0), x и VNMOрассчитаем t(x) по уравнению (3.1). Допустим, что оно равно ЮОЗмс. Если шаг дискретизации был равен 4мс, это время соответствует индексу дискретизации (sample index), равному 250.25. Следовательно, необходимо рассчитать амплитуду при этом времени, используя амплитуды на соседних целочисленных выборках. [c.5]
Для плоской ОП, перекрываемой однородной средой, гиперболу отражения можно исправить за вынос, если в уравнении поправки за нормальное приращение используется правильная скорость в среде. На рис.3.8 видно, что если используется более высокая скорость, чем в действительности (2264м/с), гипербола сглаживается не полностью. Это называется недокоррекцией. С другой стороны, если используется более низкая скорость, происходит перекоррекция. На рис.3.8 показана основа общепринятого скоростного анализа. Поправка за нормальное приращение применяется к входным выборкам ОСТ с использованием ряда опытных постоянных скоростей в уравнении (3.2). Скорость, которая наилучшим образом сглаживает гиперболу отражения, - это скорость, которая наилучшим образом корректирует за нормальное приращение перед суммированием трасс в выборке. Более того, для простого случая одной горизонтальной ОП эта скорость также равна скорости в среде над ОП. [c.7]
Смотреть страницы где упоминается термин Нормальное приращение
: [c.47] [c.42] [c.43] [c.51] [c.53] [c.207] [c.4] [c.4] [c.5] [c.7] [c.10]Смотреть главы в:
Скоростной анализ, статические поправки, суммирование -> Нормальное приращение

![Рис.3.6 Поправка за нормальное приращение [уравнение (3.2)] включает определение положения времени пробега при ненулевом выносе t(x) на времени пробега при нулевом выносе 1(0). (а) До поправки за нормальное приращение (Ь) после поправки за нормальное приращение.](/pic1/000172059236002030028094006186211214199131196223.png)