В частности, при экспоненциальных законах возрастания новых мощностей по добыче нефти и их снижения, часто применяемых в практике пла- [c.122]
В нашем случае для технологических изделий объективные причины не позволяют пользоваться этими законами распределения. Во-первых, условием получения нормального закона являются совместные действия множества случайных факторов, ни один из которых не является доминирующим. Этому не соответствуют условия эксплуатации и выбраковки изделий технологического назначения, где обязательно фигурируют доминирующие факторы. Во-вторых, для экспоненциального закона обязательны условия ординарности, стационарности и последействия, которые зачастую не выполняются для этих изделий. В частности, поток отказов их нельзя считать стационарным вследствие меняющегося во времени вероятностного режима его. [c.45]
Во-вторых, для экспоненциального закона обязательны условия ординарности, стационарности и последействия, которые часто не выполняются для этих изделий. В частности, поток отказав их нельзя считать стационарным вследствие меняющегося во времени вероятностного режима его. [c.62]
Полученные значения КПД по узлам подставляем в соответствующее приведенное уравнение насосного агрегата. где T),,T n,ijM -изменяются по экспоненциальному закону по времени, [c.164]
Если k > 1, экспоненциальный тренд выражает тенденцию ускоренного и все более ускоряющегося возрастания уровней. Такой характер свойствен, например, размножению организмов при отсутствии ограничения со стороны среды кормов, пространства, хищников, болезней. При росте по экспоненте абсолютный прирост пропорционален достигнутому уровню. Так росло население Земли в эпоху демографического взрыва в XX столетии сейчас этот период заканчивается и темп роста населения стал уменьшаться. Если бы он остался на уровне 1960 - 1970 гг. т. е. около 2% прироста в год от 1985 г., когда население составило 5 млрд чел., то к 2500 г. население Земли достигло бы уровня 5 млрд 1,02515 = 134 трлн 286 млрд человек на 1 человека приходилось бы примерно 1 м2 всей площади суши. Ясно, что рост любого объекта по экспоненциальному закону может продолжаться только небольшой исторический период времени, ибо ресурсы для любого процесса развития всегда встретят ограничения. [c.324]
Развитие по экспоненте. Экспоненциальное сглаживание временных рядов - модификация метода наименьших квадратов для анализа временных рядов, при котором более поздним наблюдениям придается больший вес, иными словами, веса точек ряда убывают (экспоненциальный закон) по мере удаления в прошлое. [c.175]
Для достоверной оценки количественных характеристик результатов анализа устанавливается минимальный объем выборки (количество фиксируемых наблюдений) с заданной точностью величины надежности в зависимости от вероятного закона распределения наблюдений. Например, предварительный анализ показал, что результаты наблюдений (выборки) подчиняются экспоненциальному закону распределения. Тогда требуемое количество наблюдений (объем выборки) определяется по формуле [c.40]
Непрерывная случайная величина X имеет показательный (экспоненциальный) закон распределения с параметром Я,, если ее плотность вероятности имеет вид [c.34]
Характеристики системы можно получить в явной аналитической форме, если принять предположение о том, что входящий поток заявок - пуассоновский и длительность обслуживания распределена по экспоненциальному закону со средним 6. [c.110]
В общем случае интенсивность отказов может не подчиняться экспоненциальному закону распределения. Тогда указанное выражение примет вид [c.215]
Функции плотности (рис. 5) и функции распределения экспоненциального закона имеют вид [c.24]
| Рис. 5. Функция плотности экспоненциального закона. | 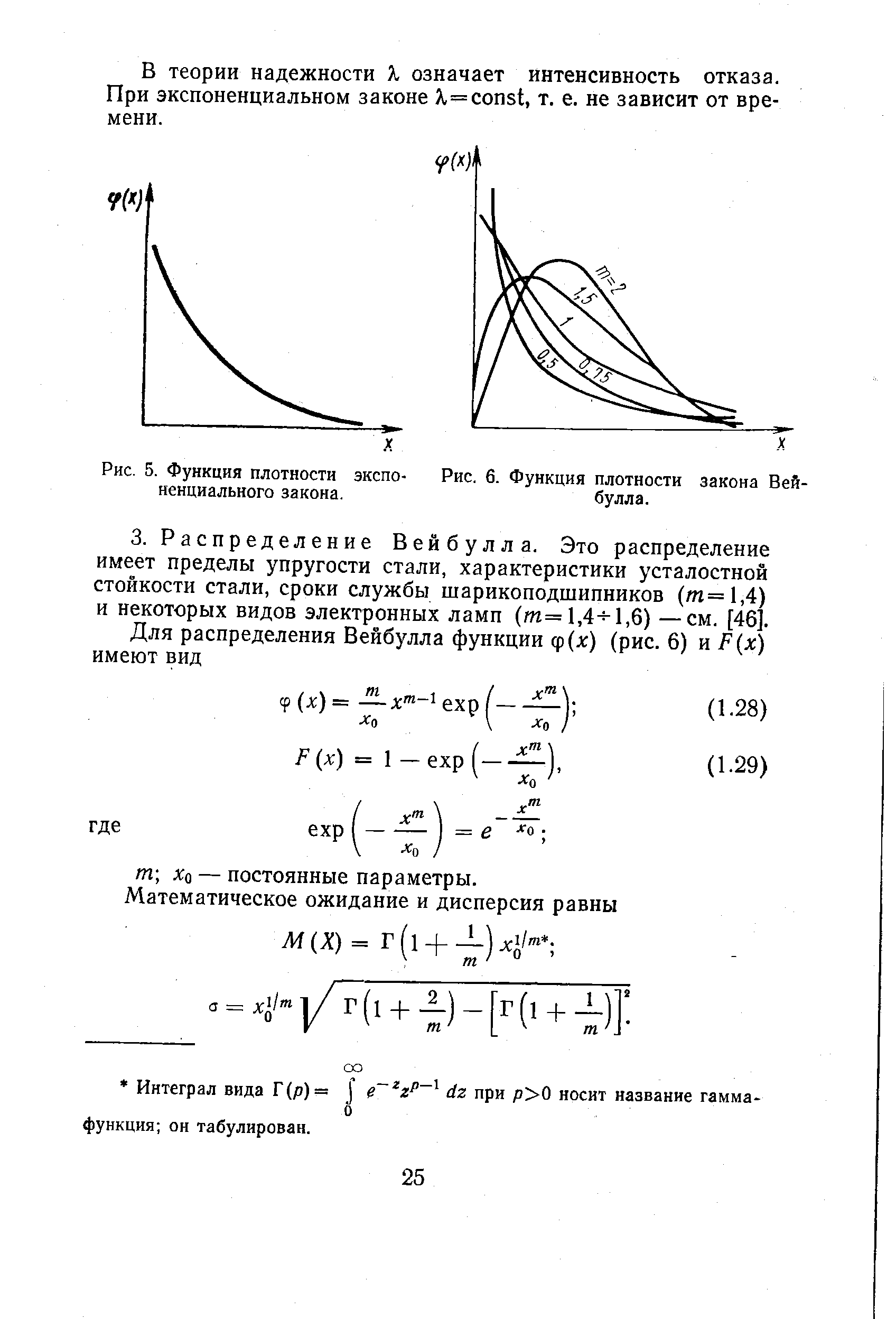 |
Я. Б. Шор [46] дает следующую формулу для определения доверительного интервала для генеральной средней в случае распределения случайной величины по экспоненциальному закону [c.39]
Если наработки на отказ подчинены экспоненциальному закону [см. (1.26)], то величина A, (t) является постоянной и не зависит от t, т. е. [c.53]
Если время отказов каждого элемента подчинено экспоненциальному закону с интенсивностью отказов Ki, то- [c.120]
В действительности, распределения приращений цен не является гауссовским, как показано на Рис. 17. Если бы это было так, то должно было проявиться в виде перевернутой параболы на этом полулогарифмическом графике. Линейная аппроксимация наблюдаемой зависимости скорее может интерпретироваться как зависимость, приближающаяся к экспоненциальному закону. В этом новом улучшенном представлении, мы можем снова вычислить вероятность наблюдения амплитуды приращения большей, чем, скажем, 10 стандартных отклонений (10% в нашем примере). Результат - 0.000045, который соответствует одному событию за 22,026 дня или 88 лет. Рост цен 20 октября 1987, в свете этого, становится менее экстраординарным. Однако, падение цен на 22.6% 19 октября 1987 соответствовало бы одному случаю за 520 миллионов лет, что позволяет интерпретировать его как " выброс". [c.62]
Вероятность безотказной работы, R, т.е. вероятность того, что в пределах заданной наработки (продолжительности функционирования изделия) отказ изделия не возникает. Вероятность безотказной работы выражается экспоненциальным законом надежности [c.37]
Нижние цифровые индексы символов J и %2 расшифровываются следующим образом первый индекс указывает номер закона распределения, которому подчиняется генерируемая последовательность чисел второй — номер гипотетического закона распределения, с которым сравнивается эмпирическое распределение. Законы распределения пронумерованы так 1 — закон Гаусса, 2 — закон Рэлея, 3 — закон Максвелла, 4 — экспоненциальный закон, 5 —- модуля нормального центрированного, 6 — закон Вей-булла с параметром у = 1,5. [c.35]
Пример 4. Выравнивание эмпирического распределения по экспоненциальному закону. [c.48]
На практике чаще других используют вероятностные модели управления запасами, основанные на том, что основные параметры систем управления — случайные величины. Это прежде всего относится к потреблению, поступлению материалов и интервалу между поставками. Распределение этих параметров управления запасами подчинено, как правило, нормальному или экспоненциальному закону. [c.406]
Полученная формула непрерывного начисления процентов выражает показательный (экспоненциальный) закон роста (при р > 0) или убывания (при р < 0). [c.99]
По определению интенсивность перехода (параметр А, экспоненциального закона распределения) имеет размерность 7//, где / - среднее время перехода элемента системы из состояния в состояние. [c.341]
Таким образом, детерминированная задача, эквивалентная стохастической задаче с вероятностными ограничениями, в которой случайные составляющие вектора Ъ независимы между собой и распределены по экспоненциальному закону, оказывается задачей. линейного программирования. [c.73]
Вероятность такого отказа (Q) в течение некоторого интервала времени (Т) при экспоненциальном законе надежности может быть оценена следующим образом [c.9]
Рассмотрим числовые модели, иллюстрирующие вышесказанное. Предположим, что связь между факторами задана линейной функцией R=2X. Если динамика показателя R описывается экспоненциальным законом = 2-1,2, то закон изменения X также является показательным Х=1,2. [c.87]
Не стоит уподобляться нерадивой студентке. Необходимо четко себе представлять, с какими объектами вы работаете. Если вы используете в своей работе при анализе графиков экспоненциально скользящие средние и утверждаете, что они более предпочтительны, чем обыкновенные средние, то полезно знать, в чем выражается это предпочтение (для экспоненциально скользящих средних влияние далеких значений цен убывает по экспоненциальному закону). [c.186]
Вместо одной из рассмотренных выше систем весов рассмотрим целый ряд весов, убывающих во времени по экспоненциальному закону. - - - - -= -- - [c.20]
Тем не менее, моделирование легкого, основанное на характерном масштабе, игнорирует прочие свойства. В пределах каждого поколения фактические диаметры имеют диапазон некоторые больше, а некоторые меньше среднего числа. Кроме того, экспоненциальный закон подобного преобразования соответствует только первым десяти поколениям ответвлений. Помимо этого, существует систематическое отклонение от характерной функции масштаба. [c.23]
Такая схема изменения функции K(t) позволяет считать, что для многих элементов машины она постоянна на протяжении всего периода их работы (периодом приработки можно пренебречь, учитывая контрольные испытания, предшествующие запуску машины в эксплуатацию). Отсюда формула надежности, подчиняясь экспоненциальному закону, и все остальные связанные с надежностью показатели могут быть выражены проще [c.146]
Поглощение лучистой энергии, подчиняющееся экспоненциальному закону [c.179]
Универсальность данного закона объясняется тем, что при различных значениях параметра b он приближается к ряду законов распределения. В частности, при b = 1 он превращается в экспоненциальный закон, при b = 2 — в закон Релея, при b — = 3,25 — близок к нормальному. Зто обстоятельство позволяет использовать один и тот математический аппарат при исследовании самых различных потоков отказов изделий. Кроме того, этот [c.45]
В ряде исследований утверждается, что для отказов технических изделий вследствие износа, усталости, коррозии и старения вполне удовлетворительным будет нормальный или логарифмически нормальный закон распределения, в случае же внезапных отказов, возникающих вследствие случ-айных перегрузок, аварий и т. д., подходит экспоненциальный закон распределения [14]. [c.62]
Универсальность данного закона объясняется тем, что при различных значениях параметра b он приближается к ряду законов распределения. В частности, при Ь = он превращается в экспоненциальный закон, при 6=2 — в закон Релея, при Ь = = 3,25 — близок к нормальному. [c.63]
В теории надежности К означает интенсивность отказа. При экспоненциальном законе К= onst, т. е. не зависит от времени. [c.25]
| Рис. 142. Левый график индонезийский пузырь, закончившийся в январе 1994 года, с параметрами соответствия логопериодическому экспоненциальному закону пЫ),44, t =1994,09, а ш=15,6. Правый график периодограмма Ломба колебательного компонента рыночной цены, приведенной на левом графике. Абсцисса является логочастотой f, где т=ш/2тт. Источник [218]. | ![Рис. 142. Левый график индонезийский пузырь, закончившийся в январе 1994 года, с параметрами соответствия логопериодическому экспоненциальному закону пЫ),44, t =1994,09, а ш=15,6. Правый график периодограмма Ломба колебательного компонента <a href="/info/5890">рыночной цены</a>, приведенной на левом графике. Абсцисса является логочастотой f, где т=ш/2тт. Источник [218].](/pic1/103103233147225157189118247221134251021063154032.png) |
| Рис. 143. Левый прафик индонезийский пузырь на фондовом рынке, закончившийся в 1997 году, с параметрами соответствия логопериодическому экспоненциальному закону пЫЩ t =1 998,05, а ш=10,1. Правый прафик периодопрамма Ломба колебательного компонента рыночной цены, приведенной на левом графике. Источник [218]. | ![Рис. 143. Левый прафик индонезийский пузырь на <a href="/info/6206">фондовом рынке</a>, закончившийся в 1997 году, с параметрами соответствия логопериодическому экспоненциальному закону пЫЩ t =1 998,05, а ш=10,1. Правый прафик периодопрамма Ломба колебательного компонента <a href="/info/5890">рыночной цены</a>, приведенной на левом графике. Источник [218].](/pic1/093006127237226096235132188175211217073087037174.png) |
| Рис. 144. Левый график корейский пузырь на фондовом рынке, закончившийся в 1994 году, и приведенный в соответствие по формуле логопериодического экспоненциального закона, где ГЛ2=1,05, t =1994,87, a (0=8,15. Правый график периодограмма Ломба колебательного компонента рыночной цены, приведенной на левом графике. Источник [218]. | ![Рис. 144. Левый график корейский пузырь на <a href="/info/6206">фондовом рынке</a>, закончившийся в 1994 году, и приведенный в соответствие по формуле логопериодического экспоненциального закона, где ГЛ2=1,05, t =1994,87, a (0=8,15. Правый график периодограмма Ломба колебательного компонента <a href="/info/5890">рыночной цены</a>, приведенной на левом графике. Источник [218].](/pic1/149063200019055077171210071038103211247162136222.png) |
| Рис. 145. Левый график малазийский пузырь на фондовом рынке, закончившийся крахом в январе 1994 года, и приведенный в соответствие формуле логопериодического экспоненциального закона, где пЫДО, t =1994,02, а w=10,9. Правый график периодограмма Ломба колебательного компонента рыночной цены, приведенной на левой панели. Источник [218]. | ![Рис. 145. Левый график малазийский пузырь на <a href="/info/6206">фондовом рынке</a>, закончившийся крахом в январе 1994 года, и приведенный в соответствие формуле логопериодического экспоненциального закона, где пЫДО, t =1994,02, а w=10,9. Правый график периодограмма Ломба колебательного компонента <a href="/info/5890">рыночной цены</a>, приведенной на левой панели. Источник [218].](/pic1/162213097040172069144049115214223251058095105137.png) |
Пусть, в частности, составляющие 6< вектора ограничений распределены по экспоненциальному закону с параметрами А,, и р,-. Экспоненциальное распределение получается из распределения Вейбулла при f = l. Ограничения (2.2) и (2.5), эквивалентные условию (2.3) задачи (2.1) — (2.3), могут быть в этом случае записаны в виде [c.73]
