Экспоненциальное, или экспоненциально сглаженное, скользящее среднее определяется путем добавления к вчерашнему значению скользящего среднего определенной доли сегодняшней цены закрытия. В случае экспоненциальных скользящих средних больший вес имеют последние цены закрытия. [c.200]
Рассчитайте n периодное экспоненциальное скользящее среднее скользящего среднего, полученного по п. 1. [c.240]
Приведенный нами пример показывает, как высчитывается простое десятидневное среднее скользящее цены закрытия. Однако существуют и другие, гораздо более сложные виды средних скользящих. Существует множество вопросов относительно того, как наилучшим образом использовать средние скользящие. Например существует ли оптимальная временная протяженность периода расчета усредненных показателей Какие средние значения следует использовать кратковременные или долговременные Существуют ли оптимальные средние скользящие для всех рынков или для каждого рынка в отдельности Является ли цена закрытия наиболее оптимальной ценой, которую следует учитывать Не лучше ли использовать несколько средних скользящих Какой тип средних скользящих лучше простой, линейно взвешенный или экспоненциально сглаженный Существуют ли периоды, в которые эти показатели более значимы, чем в остальное время [c.208]
| Рис. 9.26 Сравнительный пример двадцатидневных средних скользящих линейно-взвешенного (сплошная линия) и экспоненциально-сглаженного (пунктир). Экспоненциально-сглаженная кривая является также взвешенной, однако учитывает всю предшествующую динамику цен. Больший вес также придается показателям цен за последние дни. | 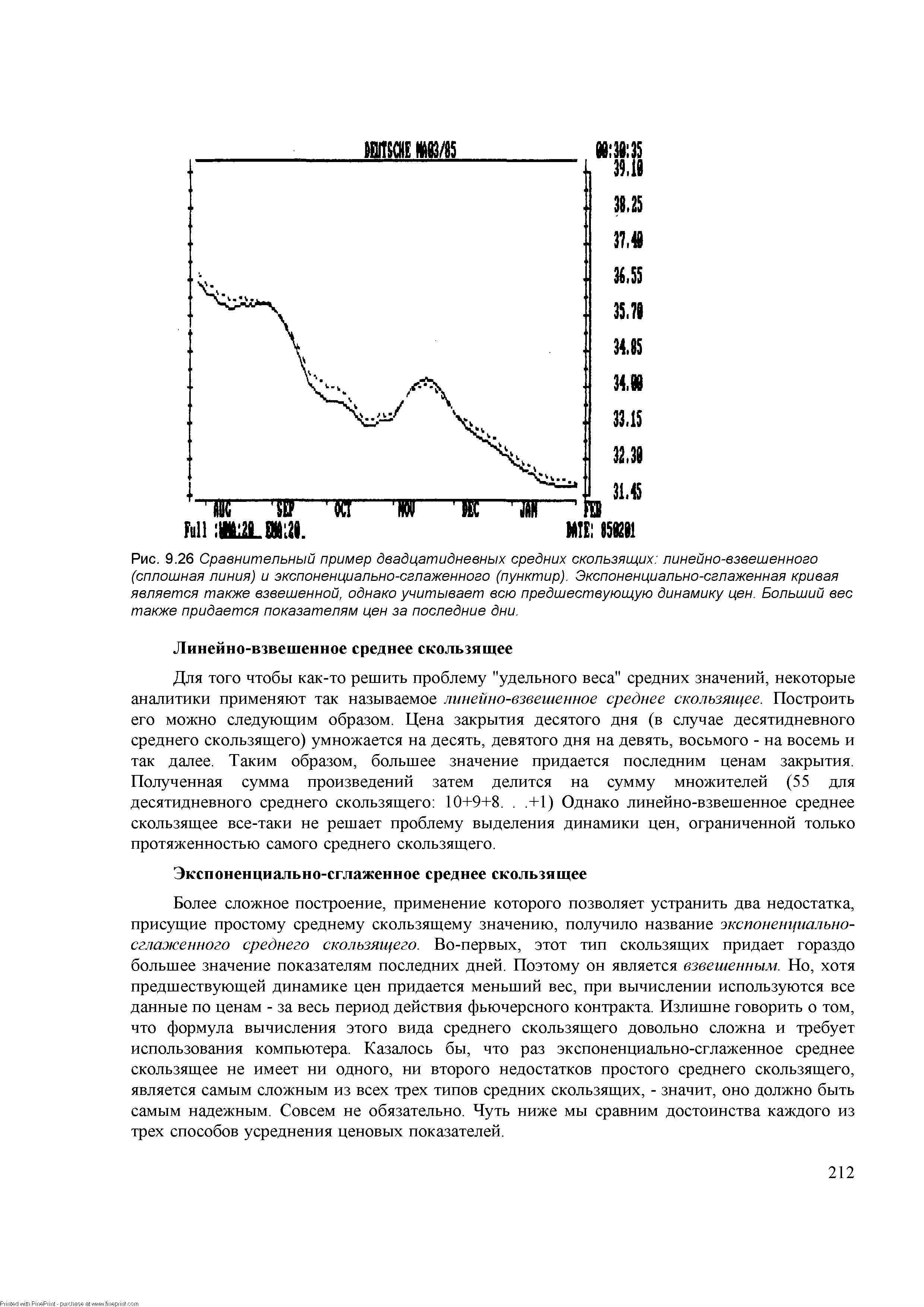 |
Более сложное построение, применение которого позволяет устранить два недостатка, присущие простому среднему скользящему значению, получило название экспоненциально-сглаженного среднего скользящего. Во-первых, этот тип скользящих придает гораздо большее значение показателям последних дней. Поэтому он является взвешенным. Но, хотя предшествующей динамике цен придается меньший вес, при вычислении используются все данные по ценам - за весь период действия фьючерсного контракта. Излишне говорить о том, что формула вычисления этого вида среднего скользящего довольно сложна и требует использования компьютера. Казалось бы, что раз экспоненциально-сглаженное среднее скользящее не имеет ни одного, ни второго недостатков простого среднего скользящего, является самым сложным из всех трех типов средних скользящих, - значит, оно должно быть самым надежным. Совсем не обязательно. Чуть ниже мы сравним достоинства каждого из трех способов усреднения ценовых показателей. [c.212]
Пока мы говорим преимущественно о простом среднем скользящем, которое отличается от линейно-взвешенного или экспоненциально-сглаженного (далее в этой главе мы [c.217]
Мы рассмотрели три типа среднего скользящего значения простой, линейно-взвешенный и экспоненциально-сглаженный. Кроме того, мы изучили различные комбинации таких показателей - применение одного среднего скользящего, а также комбинации двух или трех. При этом возник ряд вопросов. Разберем некоторые их них. [c.224]
Простое среднее скользящее оказалось эффективнее, чем линейно-взвешенное и экспоненциально-сглаженное. Оно наилучшим образом отражало динамику цен на десяти рынках (из тринадцати, на которых проводилось исследование), на двух - эффективнее оказалось линейно-взвешенное, а экспоненциально-сглаженное - только на одном, на рынке какао (см. табл. 9.4). [c.225]
| Таблица 9.3 Сводная таблица результатов тестирования экспоненциально-сглаженных средних скользящих | 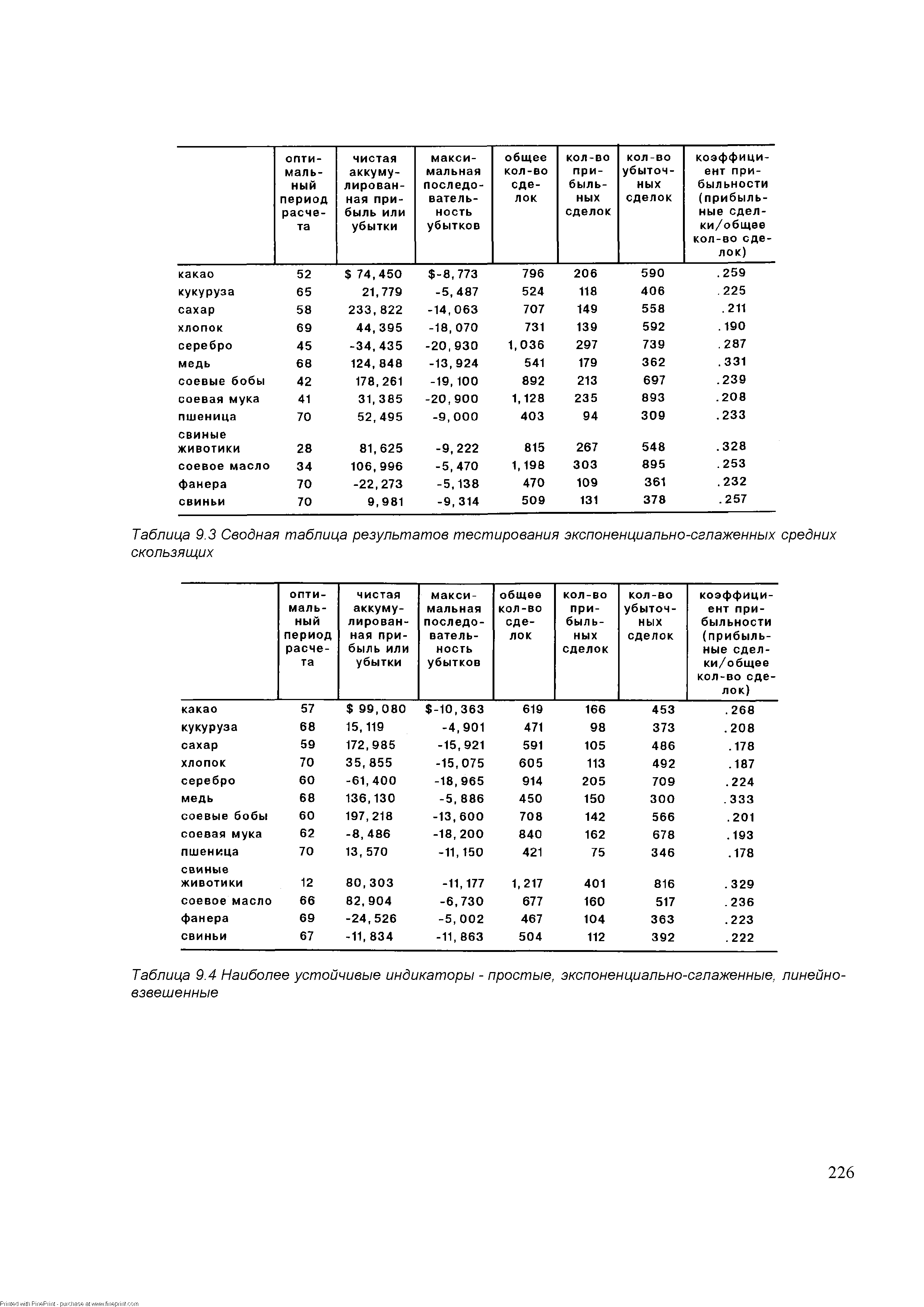 |
Потенциальный недостаток этого метода заключается в том, что в нем самые старые и последние показатели имеют равную значимость, а показатели, вышедшие за рамки расчета среднего, не учитываются вовсе. При расчете экспоненциально взвешенного скользящего среднего, или при экспоненциальном сглаживании, вклад показателя в прогноз уменьшается по мере его старения, так что наиболее свежие данные оказывают наибольшее влияние. Формула расчета экспоненциально взвешенного скользящего среднего следующая [c.143]
Часто используемым методом является также метод экспоненциального сглаживания, обобщающий метод скользящего среднего. Скользящее среднее вычисляется по формуле [c.329]
Хотя простое скользящее среднее распространено больше прочих, некоторые аналитики предпочитают делать более весомой последнюю по времени цену. Эта идея лежит в основе взвешенного скользящего среднего, при расчете которого более поздним ценам придается больший вес, а более ранним — меньший. По этой причине кривая взвешенного скользящего среднего чувствительнее, чем кривая простого, и она точнее повторяет движение цены. Наиболее распространенный вариант взвешенного скользящего среднего — это экспоненциально сглаженное скользящее среднее. При его расчете сначала определяется процентная значимость цены последнего дня, которая затем прибавляется к некоторому проценту величины индикатора за предыдущий день. Допустим, значимость цены закрытия последнего дня равна 0,10. Следовательно, она оценена в 10%, и эта величина затем прибавляется к 90% величины предыдущего дня. Показатель 0,05 даст меньший вес цене последнего дня (5%) и больший — величине индикатора за предыдущий день (95%). Чем выше процентная значимость последней цены, тем чувствительнее кривая к текущей ценовой динамике. [c.95]
Для многих индикаторов применяются сглаженные средние их предварительных расчетов, что замедляет выход данных и фильтрацию индивидуальной информации, предоставляющей ложные сигналы. Свинг-трейдеры применяют эти средние скользящие в различных вариантах для перехода от классических формул к реальным условиям. Экспоненциальные МА дают множество уникальных вариаций. Этот индикатор включает в себя большую часть входных данных предыдущего периода и фильтрует дважды просчитанную тенденцию простых средних скользящих (МА). Поэкспериментируйте с альтернативным вариантом расчета МА, когда индикаторам необходим сглаженный вид. Дифференцированные данные на выходе могут существенно усилить каждую отдельно взятую тактику или метод. Используйте выбранные на Ваше усмотрение технические индикаторы, в зависимости от того, нужно ли Вам ускорить, замедлить или отфильтровать те или иные данные. [c.294]
Для более наглядного сравнения средних между собой на рис. 1.3. 2 приведены простая, взвешенная и экспоненциальная средняя для графика курса йены с периодом, равным 2 1. Ш Вычисление экспоненциальных скользящих средних [c.11]
Формулы (25.5) так хорошо подобраны, что графики простой и экспоненциально взвешенных скользящих средних не слишком сильно отличаются друг от друга для не слишком больших одинаковых периодов га, и вопрос Что лучше, а что хуже относится к вопросам вкуса и привычки. Заметим лишь, что для больших периодов (я> 100), как правило, используются простые средние без взвешивания. Для средних и малых значений трейдеры и аналитики чаще предпочитают пользоваться экспоненциально взвешенными средними. [c.262]
Является индикатором скорости цены с преобладающим весом последних данных, для расчёта которого требуется только один временной ряд (акции, фьючерсный контракт или индекс). Метод расчёта RSI позволяет избежать проблем связанных с использованием устаревших данных. Рассчитывается на основе отношения экспоненциального скользящего среднего приростов цены (длинной п периодов) к экспоненциально сглаженному скользящему среднему паданий цены (длинной п периодов). [c.48]
В этих формулах а обозначает скользящее среднее для точки данных г, s . — точку данных номер г в последовательности, т — период скользящего среднего и с (обычно приравненное к 2/(т+ 1)) — коэффициент, указывающий эффективный период экспоненциального скользящего среднего. Уравнения показывают, что скользящие средние различаются по методу определения удельного веса точек данных. Экспоненциальные средние присваивают больший удельный вес более новым данным, а вес старых [c.133]
В пределах выборки по показателю средней прибыли со сделки наилучшие результаты дали системы на основе простого скользящего среднего, наихудшие — на основе адаптивного скользящего среднего. Другие два варианта скользящих средних дали промежуточные результаты, причем экспоненциальное среднее работало лучше в моделях на основе пе- [c.145]
Специалисты по техническому анализу биржевого рынка сокращенно называют конвергенцию-дивергенцию среднего скользящего — MA D. Как правило, этот индикатор вычисляется на основе значения экспоненциального среднего скользящего (СС), соответственно, за 26 и 12 дней его значение за 26 дней вычитается из аналогичного показателя за 12 Это центральная линия, которая осциллируется ниже или выше нуля. Если она находится выше него, то и экспоненциальное СС за 12 дней оказывается выше такого показателя за 26 дней Если же центральная линия оказывается ниже нуля, экспоненциальное СС за 26 дней тоже превышает аналогичный показатель за 12 дней (рис 1111) [c.259]
Averages). Осциллятор Схождение-расхождение скользящих средних (сокращенно MA D) основан на применении экспоненциально сглаженных скользящих средних. Этот индикатор представляет собой сочетание разности двух ЭСС ( короткого и длинного ) и третьего - самого короткого , осциллирующих относительно нулевой линии. Реальный пример MA D приведен на рис. 4.64. [c.59]
ТРИКС (TRIX) — динамический индикатор, который показывает относительную скорость изменения трижды экспоненциально сглаженного скользящего среднего цен закрытия. Он позволяет торговать в направлении тенденций с длительностью больше или равной выбранному числу периодов. [c.239]
Рассмотрим результаты исследований, полученные этой группой, и их практическое применение в анализе рынка с помощью средних скользящих. Хокхаймер опубликовал некоторые первоначальные результаты исследований в статье под названием "Компьютеры помогут вам в игре на фьючерсных рынках". Эта статья была опубликована в 1978 году в ежегоднике "Коммоди-тиз". С 1970 по 1976 год были протестированы средние скользящие по каждому месяцу исполнения по тринадцати наименованиям товарных активов. Временной промежуток, покрываемый средними скользящими, которые были использованы в исследовании, составлял от трех до семидесяти дней. Данные тестов по простым, линейно-взвешенным и экспоненциально-сглаженным средним скользящим были сведены в таблицы по отдельности с целью определения оптимального значения для каждого рынка (см. табл. 9.1-9.3). Полученные результаты были, в свою очередь, сведены в сравнительную таблицу (см. табл. 9.4) с целью определения наиболее эффективного из трех типов средних скользящих. [c.224]
| Рис. 10.19а Пример метода MA DTM. Фактически метод может использоваться либо как осциллятор, либо как индикатор, следующий за тенденций, либо в обоих качествах одновременно. Сигналами купли-продажи являются пересечения двух экспоненциально сглаженных средних скользящих. Пересечение обеими кривыми нулевого уровня также может служить сигналом к действию. На графике осциллятора хорошо видны расхождения. Обратите внимание на четкий сигнал к покупке, поступивший в декабре, когда кривые MA DTM прорвали долгосрочную нисходящую линию тренда. Поднимаясь, сплошная линия сначала пересекла пунктирную, а затем преодолела и нулевую отметку. | 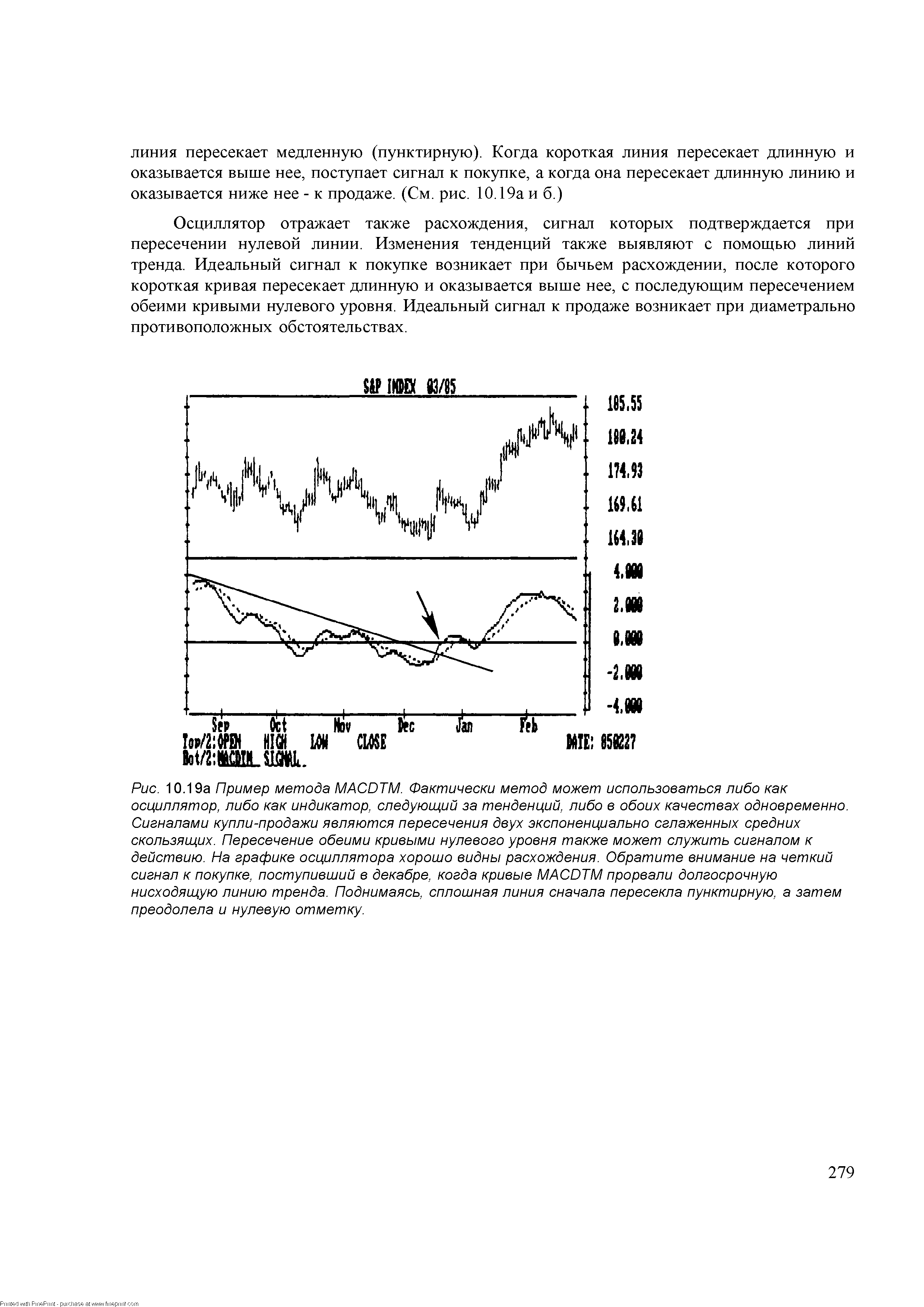 |
Схождение/расхождение скользящих средних (MA D lines) — индикатор схождения/расхождения скользящих средних, разработанный Джералдом Аппелем, представляет собой две кривых. Первая — разность между двумя скользящими средними с периодами 12 и 26 дней, построенными по ценам закрытия. Вторая — сигнальная линия — 9-дневное экспоненциально сглаженное скользящее среднее индикатора. Сигналы возникают при пересечении двух линий. [c.324]
В этом случае произвол в выборе весов ограничивается условием равенства их суммы единице. Если теперь предположить, что стационарный член со,, равен нулю, то формула (19.10) превращается в обычную рекуррентную формулу расчета (см. гл. 25, формула (25.6)) экспоненциально взвешенной скользящей средней (ЕМЛ) квадрата волатплыюсти [c.208]
Инструментом, свободным от двух перечисленных недостатков, является так называемая H-L-волатилыюсть. Согласно определению это есть просто экспоненциально взвешенная скользящая средняя разности максимальных и минимальных цен. отнесенная к средней цене актива [c.317]
Вне пределов выборки результаты были менее закономерны. При использовании простого скользящего среднего результаты были более всего близки к полученным в пределах выборки при использовании экспоненциального среднего лимитные приказы работали хуже всего, а стоп-приказы лучше всего рыночные приказыдавали средние результаты. Вне пределов выборки при использовании треугольного скользящего среднего с передним взвешиванием стоп-приказы были самыми худшими, а лимитные приказы — наиболее эффективными. Таким образом, существует взаимодействие между скользящим средним, входом и временем. [c.146]
