Известны следующие три вида скользящих средних, применяемых при техническом анализе [c.53]
Экспоненциально сглаженное (взвешенное) скользящее среднее (ЭСС), обеспечивающее наилучшее сглаживание усредняемых данных. В дополнение к применению весовых коэффициентов, при вычислении ЭСС учитываются все предыдущие цены за время наблюдения за динамикой цен, а не только цены в выбранном интервале наблюдения. Насколько графики разных видов скользящих средних отличаются друг от друга, видно из рис. 4.53. [c.53]
Известны три вида скользящих средних [c.88]
Это основная статистика. В общем, картина не самая блестящая, но вполне солидная. Однако эти показатели не базируются на оптимальных параметрах. Что произойдет, если мы пожелаем произвести оптимизацию параметров, чтобы получить максимальную прибыль Тогда мы должны оптимизировать все три параметра одновременно, чтобы установить их наилучшую комбинацию. Поэтому я протестировал разные значения для скользящих средних с периодом от 4 до 19с приращением в 1. Для долгосрочной скользящей средней были испытаны числа от 20 до 50 с приращением 1. Каждый из этих тестов затем был проверен для различных видов скользящих средних простой, смещенной, экспоненциальной и взвешенной. [c.189]
Основной недостаток данного вида скользящей средней состоит в том, что все цены, входящие в интервал, имеют одинаковый вес вместо того, чтобы придавать большее значение действию недавних периодов по сравнению с более поздними. [c.391]
В настоящее время используются несколько видов скользящих средних. Наиболее употребимым является простое скользящее среднее, при вычислении которого берутся цены за определенное пользователем число периодов, суммируются и делятся на количество периодов. 10-дневное среднее является лишь средней ценой закрытия за последние 10 дней. Каждое последующее значение заново вычисляется на основе 10 последних дней. Это демонстрирует то, как средние скользят . Выбор количества периодов, используемых для расчета среднего, зависит от анализируемой акции или товара. Обычно это число увязано с циклом соответствующего актива, таким как четырехлетний цикл фондового рынка, сезонный цикл цены нефти, связанный с отопительным периодом, и сельскохозяйственный цикл, связанный со сбором урожая. [c.70]
Показатель качества может рассчитываться за определенный период времени, например за месяц или квартал, или в виде скользящей средней по нескольким поставкам. Он может рассматриваться как указатель действительного положения только в том случае, когда показатель рассчитан по данным нескольких поставок. Формула построена так, что она учитывает как поставленное количество изделий, так и число партий или поставок. [c.156]
В чистом виде скользящие средние обычно используются для построения фильтров (рис. 7.11—7.12) и генерации сигналов смены тренда. [c.253]
Чтобы понять идею скользящих средних, для начала необходимо обсудить временные ряды, т.е. последовательности данных, расположенных в хронологическом порядке. Например, такими данными являются ежедневные цены закрытия каких-либо акций. Они образуют последовательность точек данных , или баров , следующих друг за другом во времени. Во временном ряду серии выборка из нескольких последовательных точек данных может быть названа временным окном . Если точки данных (например, цены закрытия) в данном временном окне сложить и сумму разделить на количество этих точек данных, то получится среднее . Скользящее среднее получается тогда, когда этот процесс повторяется снова и снова при смещении временного окна вперед, точка за точкой по ряду данных. Средние, полученные таким образом, образуют новый временной ряд, новый набор упорядоченных во времени значений. Эта серия называется скользящей средней временного ряда (в данном случае — скользящее среднее цен закрытия). Этот вид скользящих средних известен как простое скользящее среднее, поскольку рассчитывается как простое арифметическое среднее точек данных, что присваивает каждой точке один и тот же удельный вес. [c.131]
| Таблица 6—3. Эффективность следующих за трендом моделей в зависимости от вида приказов, вида скользящих средних, типа модели и выборки данных | 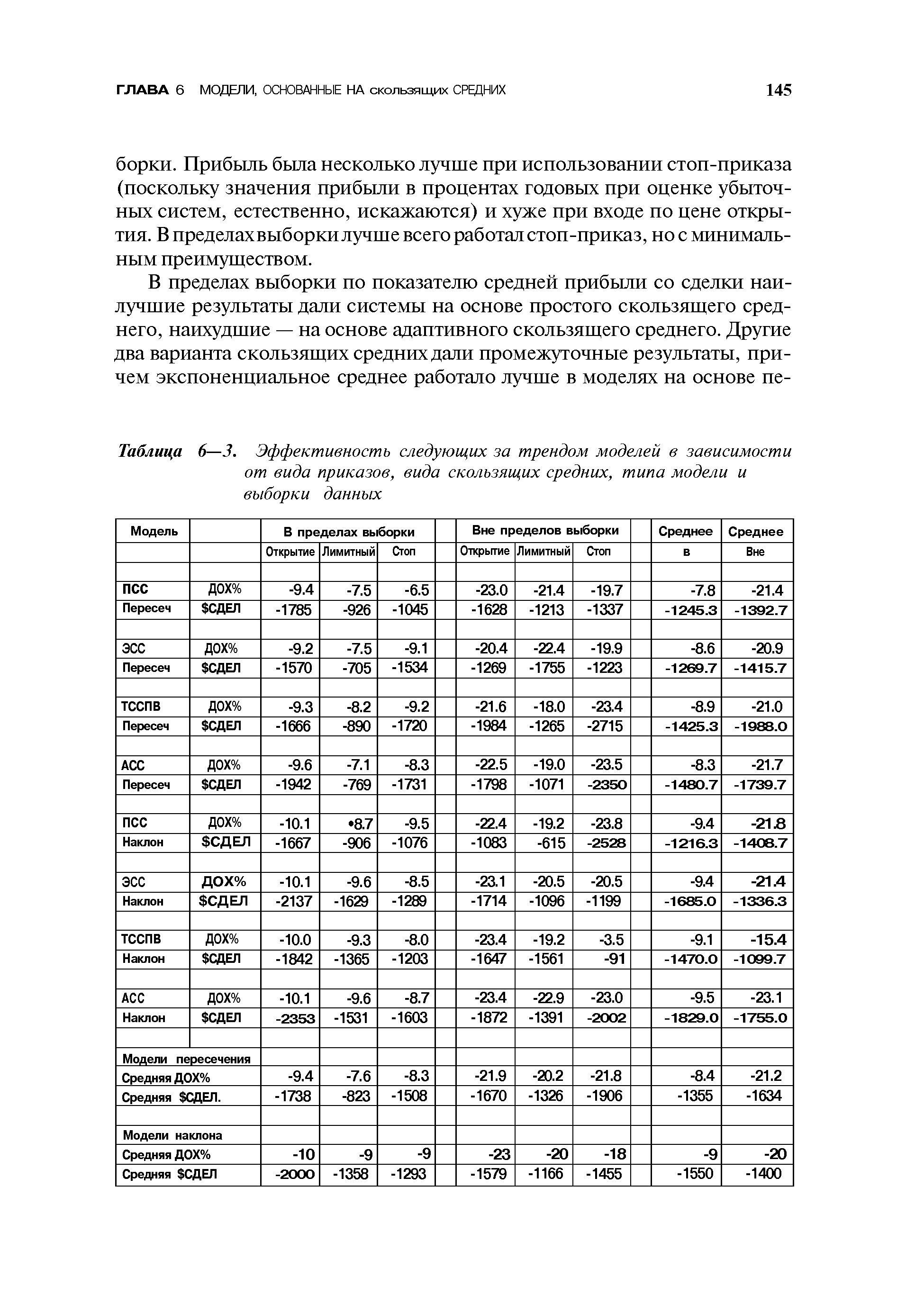 |
Представление процесса типа МА в виде процесса авторегрессии неэкономично с точки зрения его параметризации. Аналогично процесс AR не может быть экономично представлен с помощью модели скользящего среднего. Поэтому для получения экономичной параметризации иногда бывает целесообразно включить в модель как члены, описывающие авторегрессию, так и члены, моделирующие остаток в виде скользящего среднего. Такие линейные процессы имеют вид [c.45]
Имеется много различных типов скользящих средних — простые, экспоненциальные, смещенные, адаптивные и т. д., и все они могут быть использованы в качестве уровня скользящего стопа. Вашей задачей является просто найти одну или несколько скользящих средних, которые наилучшим образом отвечают вашим целям. Разные виды скользящих средних подробно обсуждались нами в главе о входах, т. е. в главе 8 этой книги. [c.283]
Модели скользящего среднего (МА) представляют стационарный процесс в виде линейной комбинации последовательных значений белого шума . Такие модели оказываются полезными как в качестве самостоятельных описаний стационарных процессов, так и в качестве дополнения к моделям авторегрессии для более детального описания шумовой составляющей. [c.105]
Для выявления циклической составляющей динамики валютного курса статистикой также используется выравнивание по ряду Фурье, поскольку циклические колебания являются разновидностью периодических, как и сезонные. Может применяться и метод скользящей средней. Период скольжения принимают, естественно, другой, соответствующий периоду циклических колебаний. В нашем примере сглаживание целесообразно проводить по 33-месячной скользящей средней (см. рис. 15.3). Период можно определить по графику и с помощью спектрального анализа, представив ряд в виде непрерывной функции, которую можно разложить на сумму бесконечного числа гармонических функций с периодом от 0 до 2л с различной амплитудой. Спектральной плотностью функции называется величина амплитуды гармоники в зависимости о г ее периода. Чем больше амплитуда (спектр) данной гармоники, тем сильнее в использованной функции присутствуют колебания с этим периодом. [c.664]
В первую очередь проверяется гипотеза о наиболее простой - линейной форме уравнения тренда, т. е. о несущественности различий цепных абсолютных изменений. Имеем 12 абсолютных изменений скользящей средней, которая хотя и сгладила сильные колебания уровней ряда, но как видим, ее абсолютные изменения далеко не одинаковы. Разбиваем эти 12 цепных приростов на два подпериода по 6 приростов в каждом, и для каждого подпериода вычисляем среднюю А , среднее квадратическое отклонение (СКО) как оценку генерального СКО с учетом потери одной степени свободы вариации, s [c.327]
На рис. 6.6 показаны исходные значения объема продаж, а также экспоненциально сглаженные значения при а = 0.1. Как видно из графика на рис. 6.6, метод экспоненциального сглаживания действительно существенно сглаживает ряд значений. И вполне логично использовать эти значения для оценки тренда в последующие годы. Однако, некоторые сложности возникают при использовании столь малых значений, как 0.1, например. Основной недостаток состоит в том, что между изменениями в исходном ряду значений и соответствующими изменениями в ряду сглаженных значений отмечается лаг (или запаздывание). Так, мы видим, что анализируемые данные демонстрируют восходящий тренд объема продаж. Однако скользящие средние медленно обозначают этот тренд. Обратите внимание, что на графике (рис. 6.6) все сглаженные значения за последние пять лет находятся под фактическими значениями объема продаж. В целом, чем меньше значение а, тем менее оно чувствительно к изменениям тренда в данном временном ряду. Чтобы решить эту проблему, мы можем взять большее значение а. Рассмотрим, например, значение сглаживающей константы, равное а = 0.3. В таблице ниже приведены сглаженные значения, рассчитанные по этой константе. [c.194]
Фильтрация данных — это процесс их преобразования с целью получения более удобного и наглядного вида для дальнейшей обработки. Можно выделить две категории — скользящие средние и осцилляторы. [c.168]
До сих пор мы старались определить на графике только точки покупки, продажи и стопов. Это — самые основы технического анализа, цель которого приучить пользоваться графиком как картой, по которой вы будете ориентироваться на рынке. Теперь, когда вы освоились с общим видом графика, пришло время добавить первый индикатор. Один из наиболее широко используемых — скользящая средняя. [c.31]
Скользящая средняя основывается на средней цене в течение определенного периода времени. Например, 200-дневная скользящая средняя — это средняя цена закрытия за последние 200 дней 50-дневная скользящая средняя охватывает предыдущие 50 дней и т. д. Скользящие средние — как и сами графики — могут применяться в любой временной структуре. Вы можете иметь 10-дневную скользящую среднюю на дневном графике или 10-минутную скользящую среднюю на внутридневном графике. Имейте в виду, чем короче период, тем "отзывчивее", вероятно, будет скользящая средняя. Иными словами, 10-дневная скользящая средняя более близко повторяет движение текущего рынка, чем 200-дневная скользящая средняя. [c.31]
Возьмите чистый график — никаких линий тренда, скользящих средних или других индикаторов. Просто смотрите на него. Что вы видите Поупражняйте глаза и ум в нахождении базовых фигур, разобранных нами к данному моменту — V, U, M, W, сжимающиеся треугольники и т. д. [c.42]
| Рис. 5.35. Примеры графиков трех видов скользящих средних— за 5 дней (white), 20 дней (red) и 60 дней (green) |  |
Moving Averages — скользящие средние. Метод скользящих средних представляет собой методику расчета среднего значения цены, или показателя индикатора за определенный период времени. Термин скользящий подразумевает, и это на самом деле так, что средняя изменяется или движется во времени. Существует несколько видов скользящих средних. Перечислим некоторые из них [c.256]
Существуют много видов скользящих средних. Мы рассмотрим три основных вида показателя среднего движения курса простой, или линейный (Simple MA), взвешенный (Weighted MA) и экспоненциальный (Exponential MA). [c.6]
При т= и модифицированный индикатор превращается в обычный. Этот индикатор впервые был реализован в торгово-аналити-ческом терминале SmartTrade. Там же предусмотрена возможность выбора вида скользящих средних простая и экспоненциально взвешенная. [c.296]
Все скользящие средние, от простых до сложных, сглаживают временные ряды с использованием некоторого усредняющего процесса. Отличия состоят в том, какой удельный вес присваивается каждой из точек данных и насколько хорошо адаптируется формула к изменению условий. Различия между видами скользящих средних объясняются разными подходами к проблеме снижения запаздывания и увеличения чувствительности. Наиболее популярные скользящие средние (см. формулы ниже) — это простое скользящее среднее, экспоненциальное скользящее среднее и треугольное скользящее среднее с передним взвешиванием. Менее распространено адаптивное скользящее среднее Чанда (1992). [c.133]
Эта группа включает модели, построенные по принципу следования за трендом, с использованием скользящих средних. Модели различаются видом скользящих средних, правилами генерации сигналов и видами приказов, обеспечивающих вход. Использовались следующие виды скользящих средних простые, экспоненциальные, треугольные с передним взвешиванием и модифицированные VIDYA. Исследованы системы простого пересечения цены и средней, пересечения двух скользящих средних, а также модели со входами на основе наклона графика скользящей средней. В качестве входов использовались лимитные, рыночные и стоп-приказы. [c.142]
В табл. 6-3 для всего портфеля приведены показатели прибыли в процентах годовых (ДОХ%) и среднего результата сделки ( СДЕЛ), распределенные по видам скользящих средних, моделей, входных приказов и выборке данных. Два правых столбца и четыре нижние строки — усредненные значения. В последней строке приведены данные, усредненные для всех сочетаний моделей и средних. Данные в правом столбце усреднены для всех видов приказов. [c.143]
Противотрендовые модели, так же как и следующие за трендом, могут использовать различные виды скользящих средних, различные правила генерации сигналов и различные виды приказов для входа в рынок. Использованы те же виды скользящих средних, что и ранее тестировались модели на основе и одиночных, и двойных скользящих средних. Использовались рыночные, лимитные и стоп-приказы. [c.148]
Противотрендовые модели работали хуже, чем следующие за трендом. Тем не менее нашлись превосходные сочетания противотрендовои модели, вида скользящих средних и приказа для входа, которые работали гораздо лучше большинства других протестированных комбинаций. [c.152]
Поскольку мы предполагаем сейчас, что xt, yt 1(1), то ряды разностей Ддс,, Ду, стационарны. Будем предполагать в дополнение, что стационарен векторный ряд (Axt, Ау<)Т, так что для него существует разложение Вольда в виде скользящего среднего [c.185]
Модель скользящей средней q-то порядка (или модель2 МА ( )), имеет вид [c.148]
Теория Хаоса постулирует, что сходные по природе модели возникают на разных масштабах. Что также истинно и для ценовых моделей на рынке. Имейте в виду, что хорошая компания не всегда означает хорошие бумаги. Например, Wal-Mart была хорошей компанией в течение многих лет, однако ее акции были "плохими" между 1993 и 1997 годами. Четыре года это большой срок ожидания того, как хорошие фундаментальные данные подтвердят сами себя. Диаграммы "крестики-нолики" помогают выявить действующие на рынке силы спроса и предложения и, тем самым, помогают инвестору различить "хорошие" акции от "плохих". И восприимчивость этих графиков к рыночной динамике делает их прекрасной основой торговых систем, использующих скользящие средние. [c.83]
Рис. 152 иллюстрирует количество короткого интереса для Intel в течение 1999. Заметьте драматическое увеличение в коротком интересе, которое имело место в апреле. Это произошло, поскольку акция отступала к поддержке на 200-дневном скользящем среднем значении в апреле и мае 1999 года. Такое увеличение показательно для подавляющего пессимизма инвесторов в отношении акции. Большой короткий интерес для акций, показывающих сильное ценовое движение с откатами, содержащими ключевые уровни поддержки - это место, где вы потенциально будете видеть быстрые, существенные повышения, вызванные закрытием коротких позиции, чтобы выкупить бумаги и ограничить потери, поскольку акция перемещается выше от поддержки. Это добавляет топлива к уже мощному повышающемуся тренду, что можно заметить в повышении INT с июня до сентября 1999 года. [c.269]
Другая особенность неустойчивого рынка типа NASDAQ — "расширения — ("extensions") — процентное изменение относительно различных скользящих средних. Например, 20-дневная скользящая средняя NASDAQ равна 2500. Если текущая цена — 2650, то это будет верхнее расширение на 6%. Нанося эти расширения на график, можно анализировать эти корреляции, чтобы видеть, когда и где рынок ненормально расширен. [c.70]
