Определяют среднюю квадратическую ошибку [c.57]
Если же показатель степени Ь — 2, то средняя глубина скважин выразится средней квадратической величиной, т. е. [c.149]
Ввиду того что зависимость VK (Я) характеризуется гиперболической кривой, средняя квадратическая величина глубин скважин более близка к их средней глубине, чем средневзвешенная величина. Для приведенного выше примера, если средневзвешенная величина для обоих УБР одинакова и составляет 2500 м, то средняя квадратическая величина для первого УБР составляет 2500 м, а для второго УБР — 2920 м. [c.149]
Следовательно, средняя квадратическая величина учитывает специфику работы второго УБР, заключающуюся в том, что 10 скважин здесь являются глубокими (4000 м), поэтому средняя глубина скважин у них больше, чем в первом УБР в 1,17 раза. [c.149]
Если зависимость VK (Я) не установлена, то для характеристики средних глубин скважин, когда индивидуальные значения их отличаются значительно, необходимо пользоваться средней квадратической величиной глубин скважин. [c.149]
Коэффициент точности относительно поля допуска, выражаемый отношением среднего квадратического отклонения 5 значений параметра к величине поля допуска, [c.155]
Контрольные карты различаются по назначению. Они могут применяться для регулирования настройки производственного процесса (карты средних арифметических значений и медиан) и для регулирования рассеяния показателей качества (карты средних квадратических отклонений, размахов, вариаций), для оценки стабильности процессов (карты кумулятивных сумм). [c.159]
Контрольные карты по количественному признаку строятся в предположении, что регулируемый параметр распределен по нормальному закону с характеристиками тх = а - математическое ожидание значения параметра а -среднее квадратическое отклонение. Это характеристики параметра в генеральной совокупности. Для построения центральной линии и границ регулирования необходимо оценить а и о по характеристикам к выборок с п числом изделий в выборке. Общее число измерений m = кп. [c.159]
Медиана выборки имеет нормальное распределение с математическим ожиданием те = а = х , и средним квадратическим отклонением а л/ п / 2п = 1,25 а. Следовательно, интервал регулирования карты х несколько [c.163]
Чаще всего применяют карту средних арифметических значений и выборочных средних квадратических отклонений (карта х/а ). В ней помещаются отдельные графики средних арифметических значений х и выборочных средних квадратических отклонений G. Границы регулирования параметра с устанавливаются расчетом по формуле [c.163]
Карта средних квадратических от- v [c.169]
Характеристика погрешности от неоднородности СО выражается в виде среднего квадратического отклонения сгн в соответствии с [c.22]
Разброс значений выходных сигналов 1т и погрешность определения среднего / зависят от величины случайной погрешности аналитического прибора и однородности СО. Характеристикой этой погрешности может служить среднее квадратическое отклонение сг , [c.45]
Чем меньше К и, соответственно, чем ближе X, к единице, тем лучше правая часть уравнения (2) аппроксимирует значению уровня издержек обращения. По данным таблицы получены следующие результаты средних х, средних квадратических отклонений а,- и парных коэффициентов а// [c.154]
Операторы 2 — 20. Вычисление математических ожиданий и средних квадратических отклонений для исследуемых факторов раздельно по типам буровых установок. Здесь и далее использованы следующие обозначения =1,р — тип буровой установки /=1,/п — номер исследуемого фактора, начиная от Ят-э и кончая V i=l, n — номер замера (данные по скважинам, законченным бурением) х — значение фактора х — математическое ожидание фактора S — среднее квадратическое отклонение фактора. [c.71]
Операторы 37 — 49. Вычисление математических ожиданий и средних квадратических отклонений для всех исследуемых данных при условии объединения их в одну совокупность (независимо от типа буровых установок). [c.71]
Операторы 89 -94. Проверка надежности коэффициентов регрессии уравнения для объединенной совокупности по критерию Стьюдента. В этой группе операторов выделяется подпрограмма вычисления средней квадратической ошибки коэффициентов регрессии (оператор 90). Алгоритм этой подпрограммы представлен на рис. 10. [c.75]
| Рис. 10. Алгоритм вычисления средней квадратической ошибки коэффициентов | 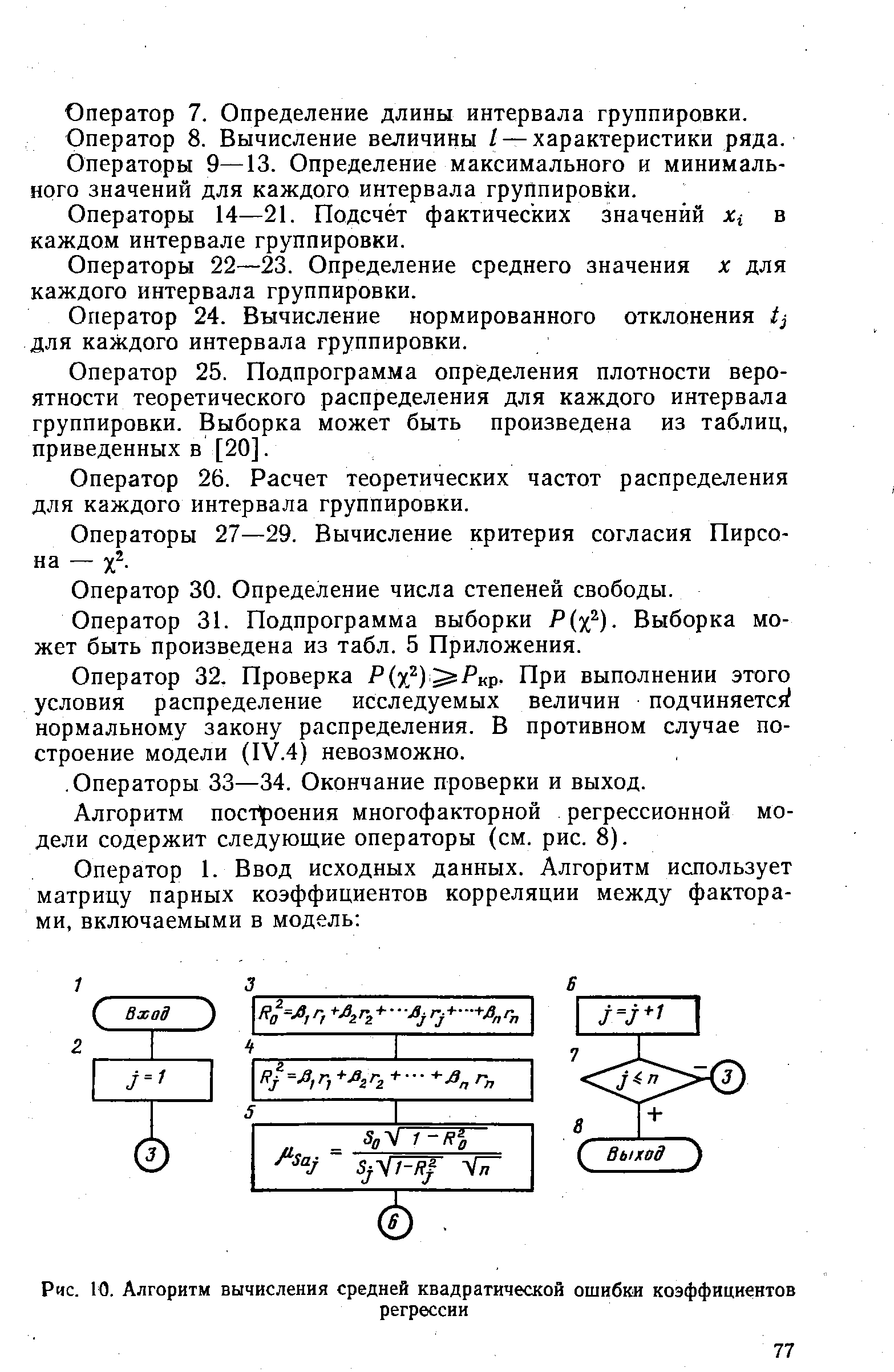 |
Операторы 5—7. Вычисление средней квадратической ошибки коэффициентов регрессии. [c.79]
Базой для формирования нетто-ставки служит показатель убыточности страховой суммы, который определяется как отношение суммы страхового возмещения, выплаченной за определенный период, к страховой сумме всех застрахованных объектов за этот же период. Затем рассчитывается средний показатель убыточности с поправкой на величину рисковой надбавки (вероятность отклонения показателя убыточности от его средней величины). Для этого строится динамический рад показателей убыточности и оценивается его устойчивость с помощью показателя среднего квадратического отклонения. [c.339]
Коэффициент вариации (К ) определяется как отношение средне-квадратического отклонения от планового задания за сутки (декаду, [c.112]
Статистический анализ показывает, что уравнение значимо Рф = 5,054 при /"табл = 3,01, корреляционное отношение равно 0,9959, ее"стандартная ошибка равна 0,0015. Среднее квадратическое отклонение расчетной себестоимости от фактической равно 0,018. Средняя ошибка аппроксимации 1,1%. [c.90]
Первые четыре строчки в табл. 27 (средние значения, их ошибки, средние квадратические отклонения, коэффициенты вариации) вычислены по, всей исходной информации объединения за 1956—1970 гг. Остальные (чистые коэффициенты корреляции, автокорреляционные отношения Неймана, дифференциальные производительности и эластичности факторов) получены на базе кинетической функции (49) при средних величинах себестоимости добычи нефти и попутного газа и факторов. Среднее арифметическое значение уровня себестоимости и факторов достаточно высоки (первая строка, табл. 27). Стандартные ошибки средних значений свидетельствуют о небольшом различии между генеральными и выборочными средними значениями, что повышает статистическую достоверность последних. [c.91]
Закон распределения случайной величины, обладающей следующим свойством промежутки времени между любыми двумя соседними событиями и его среднее квадратическое отклонение равны 1/Х, где — интенсивность потока, являющегося экспоненциальным, или показательным. [c.177]
Инвестиционная деятельность всегда сопровождается риском, поскольку связана с иммобилизацией собственных финансовых ресурсов, с привлечением заемных средств, с разными сроками их возврата и ценой, поскольку инвестиции осуществляются в условиях неопределенности. Для оценки инвестиционных рисков используются статистические методы оценки, например, дисперсия, среднее квадратическое отклонение, коэффициент вариации, размах вариации и другие, так как требуется учесть неопределенность и вероятностные характеристики получения результатов не ниже требуемого значения, учесть вероятность наступления ожидаемого ущерба. [c.64]
Средневзвешенная величина глубин скважин по объединению Каспморнефть за указанные годы составляет соответственно 2818 -и 2782 м средняя квадратическая величина-—3070 и ЗОЮ м, а средняя глубина, определенная по зависимости (94), — 3090 и 3040 м. Из этих данных следует, что средневзвешенная величина значительно уменьшает среднюю глубину скважин в целом по объединению. Это уменьшение составляет за 1971 и 1972 гг. соответственно 252 и 288 м (или 8,9 и 8,2%) от средних квадратических величин и 272 и 258 м (или 9,7 и 9,3%) от средних глубин, определенных по форму ле (94). [c.150]
С помсшью СО п и метг олсгкческой аттестации анализаторов качества могут быть оценены следующие метрологические характеристики среднее квадратическое отклонение случайной составляющей погрешности сг(°Д) систематическая составляющая погрешности Дс погрешность Д. [c.53]
Операторы 2—7. Расчет математического ожидания проходки на доло то и среднего квадратического отклонения. Здесь г— порядковый номер долота / — порядковый номер стратиграфического горизонта Нц — проходка данного типоразмера г-го долота /-го горизонта h,—математическое ожидание проходки на долото /-го горизонта Shj—среднее квадратическое отклонение для проходки /-го горизонта. [c.59]
Показатели Среднее значейие Среднее квадратическое отклонение Коэффициент вариации [c.34]
Средние квадратические отклонения (третья строка, табл. 27) показывают значительные колебания показателей НГДУ около соответствующих средних, что отражает неравномерность размещения НГДУ по условиям эксплуатации нефтяных месторождений и залежей. [c.91]
