Сама функция рк может быть найдена по таблице значений нормальной функции распределения вероятностей (табл. 7.6). [c.235]
| Таблица 7.6. Значения нормальной функции распределения вероятностей |  |
Процесс определения затрат и ресурсов, необходимых для выполнения каждой работы, начинается после того, как разработан сетевой график и определен его критический путь. Таким образом, материальные и трудовые ресурсы планируются на основе общей структуры сети, созданной с помощью прогнозирования временных опенок. В то же вре-Таблица 5.1. Значения нормальной функции распределения вероятностей [c.43]
Вероятности, основанные на оценке риска, присваиваются ожидаемым денежным потокам, ожидаемая величина инвестиций определяется путем умножения вероятностей на соответствующие величины денежных поступлений. Функция распределения вероятностей может быть построена при помощи компьютера. [c.377]
При имитационном моделировании менеджер получает функции распределения вероятностей для набора переменных - параметров моделирования (например, поступления денежных средств в рамках инвестиций, объема продаж по количеству и т. д.). С помощью случайной выборки этих переменных по полученным распределениям можно оценить чистую текущую стоимость. Так как для получения различных результатов с помощью случайных выборок используется компьютер, имитационное моделирование относится к дорогостоящим подходам. [c.383]
Исходя из стохастической природы исследуемого объекта любую точку на графике рис. 67 можно считать исходом, имеющим некоторую вероятность для заданного объема работ, поэтому аналогом производственной функции геологоразведочных работ является двумерная функция распределения вероятностей возможных исходов. Изолинии этих вероятностей дают представление производственных функций в виде семейства кривых, каждой из которых соответствует вероятность, или показатель надежности, реализации данного направления ГРР. [c.201]
Эти параметры не полностью описывают стохастический граф с возвратом, а характеризуют его однократную реализацию. Поэтому дополнительно вводятся статистические параметры графа, описывающие его в среднем, такие, как математическое ожидание и дисперсия времени реализации проекта, вероятность совершения события не позже заданного срока, гистограммы и выборочные функции распределения вероятностей времени совершения конечного и других наиболее важных событий, а также стоимость выполнения комплекса операций. [c.197]
Во 2-й главе рассказано о наиболее употребительных законах распределения случайных величин и основных параметрах этих законов. Даны методы поиска функции распределения вероятности случайной величины в случае неинтегрируемой плотности вероятности, а также алгоритмы получения последовательностей случайных величин с произвольным законом распределения, что необходимо при моделировании случайных процессов. [c.10]
Интегральным законом., или функцией распределения вероятностей случайной величины X, называется функция, значение которой для любого х является вероятностью события, заключающегося в том, что случайная величина X принимает значения, меньшие х, то есть функция F(x) = Р Х < х . Функция [c.15]
Для случайной величины с непрерывной и дифференцируемой функцией распределения вероятностей F(x) можно найти дифференциальный закон распределения вероятностей., выражаемый как производная F(x), то есть р(х) = dF(x)/dx. Эта зависимость называется плотностью распределения вероятностей. Плотность распределения р(х) обладает следующими свойствами [c.15]
В этой главе мы рассмотрим наиболее употребительные законы распределения случайных величин, а также основные параметры этих законов. Будут даны методы поиска функции распределения вероятности случайной величины в случае неинтегрируемой плотности вероятности, а также алгоритмы получения последовательностей случайных величин с произвольным законом распределения, что необходимо при моделировании случайных процессов. Особое внимание будет уделено обобщенному экспоненциальному распределению, которое наиболее пригодно при изучении ценообразования активов. [c.30]
Для равномерного распределения можно в явном виде найти функцию распределения вероятностей F(x) = О х < а [c.34]
Плотность вероятности распределения Гаусса нельзя проинтегрировать для получения интегральной функции распределения вероятностей F(x) в явном виде. F(x) можно найти с использованием [c.35]
Из предыдущей главы мы узнали, как найти оптимальное f и его побочные продукты при нормальном распределении. Тот же метод применим к любому другому распределению, где известна функция распределения вероятности (то есть интеграл плотности распределения вероятности). О многих известных распределениях и об их функциях распределения вероятности рассказано в приложении В. [c.118]
N() = кумулятивная нормальная функция распределения вероятностей, задаваемая уравнением (3.21). [c.156]
N() = кумулятивная нормальная функция распределения вероятностей, [c.237]
| Рис. 22. Функция распределения вероятности квадрата скорости жидкости, нормализованная к ее среднему времени, в одиннадцатом слое игровой модели гидродинамической турбулентности, обсуждаемой в тексте. Вертикальная ось имеет такой логарифмический масштаб, что прямая линия, которая помогает глазу, квалифицируется, как очевидное показательное распределение. Обратите внимание на появление чрезвычайно редких и больших взрывов скоростей на краю, выше экстраполяции прямой линии. Источник [252]. | ![Рис. 22. Функция распределения вероятности квадрата скорости жидкости, нормализованная к ее среднему времени, в одиннадцатом слое игровой модели гидродинамической турбулентности, обсуждаемой в тексте. Вертикальная ось имеет такой логарифмический масштаб, что прямая линия, которая помогает глазу, квалифицируется, как очевидное <a href="/info/5302">показательное распределение</a>. Обратите внимание на появление чрезвычайно редких и больших взрывов скоростей на краю, выше экстраполяции прямой линии. Источник [252].](/pic1/205196012179108108119160056012034002236089221065.png) |
| Рис. 23. Функция распределения вероятности квадрата скорости как на Рис. 22, но для гораздо более длинного ряда времени, чтобы хвост распределений для очень больших флуктуации был намного лучше ограничен. Гипотеза о том, что не существует "выбросов" здесь проверяется "разрушением" распределения для трех показанных слоев. В то время, как это имеет успех для маленьких колебаний, хвосты распределений для больших событий весьма различны, указывая, что экстремальные колебания принадлежат к собственному классу и, следовательно, "выбросы". Вертикальная ось снова в логарифмическом масштабе. Источник [252]. | ![Рис. 23. Функция распределения вероятности квадрата скорости как на Рис. 22, но для гораздо более длинного <a href="/info/4684">ряда времени</a>, чтобы хвост распределений для очень больших флуктуации был намного лучше ограничен. Гипотеза о том, что не существует "выбросов" здесь проверяется "разрушением" распределения для трех показанных слоев. В то время, как это имеет успех для маленьких колебаний, хвосты распределений для больших событий весьма различны, указывая, что экстремальные колебания принадлежат к собственному классу и, следовательно, "выбросы". Вертикальная ось снова в логарифмическом масштабе. Источник [252].](/pic1/151255070046029077102042074146191012187176133187.png) |
Оценка — это количественное описание выявленных рисков, в ходе которого определяются такие их характеристики, как вероятность и размер возможного ущерба. В это время формируется набор сценариев развития неблагоприятных ситуаций и для различных рисков могут быть построены функции распределения вероятности наступления ущерба в зависимости от его размера. [c.17]
Интегральная функция распределения вероятности имеет при этом следующий вид [c.93]
Статистический подход к оценке инвестиционных рисков сводится к нахождению функции распределения вероятности достижения некоторой нормы доходности проекта. Задаваясь желаемой величиной доходности, можно вычислить вероятность того, что реальная доходность проекта будет не меньше заданной. И наоборот, задаваясь некоторой желаемой величиной вероятности успешной реализации проекта (например, 90 или 95%), можно определить норму доходности, которая будет достигнута с заданной вероятностью. Данный тезис иллюстрируется на рис. 12.3. [c.195]
Теперь покажем связь между функцией распределения вероятности, функцией принадлежности множеству и лингвистическими переменными. [c.96]
Используя понятие нечеткого графика, легко показать связь между функциями распределения вероятности и принадлежности к множеству, когда одна и та же функция описывается как в терминах распределения вероятности, так и в терминах принадлежности множеству. Эта связь показана на рис. 3.4 [3.18]. [c.97]
| Рис. 12. Функция распределения вероятности отсчета у цифрового измерительного прибора | 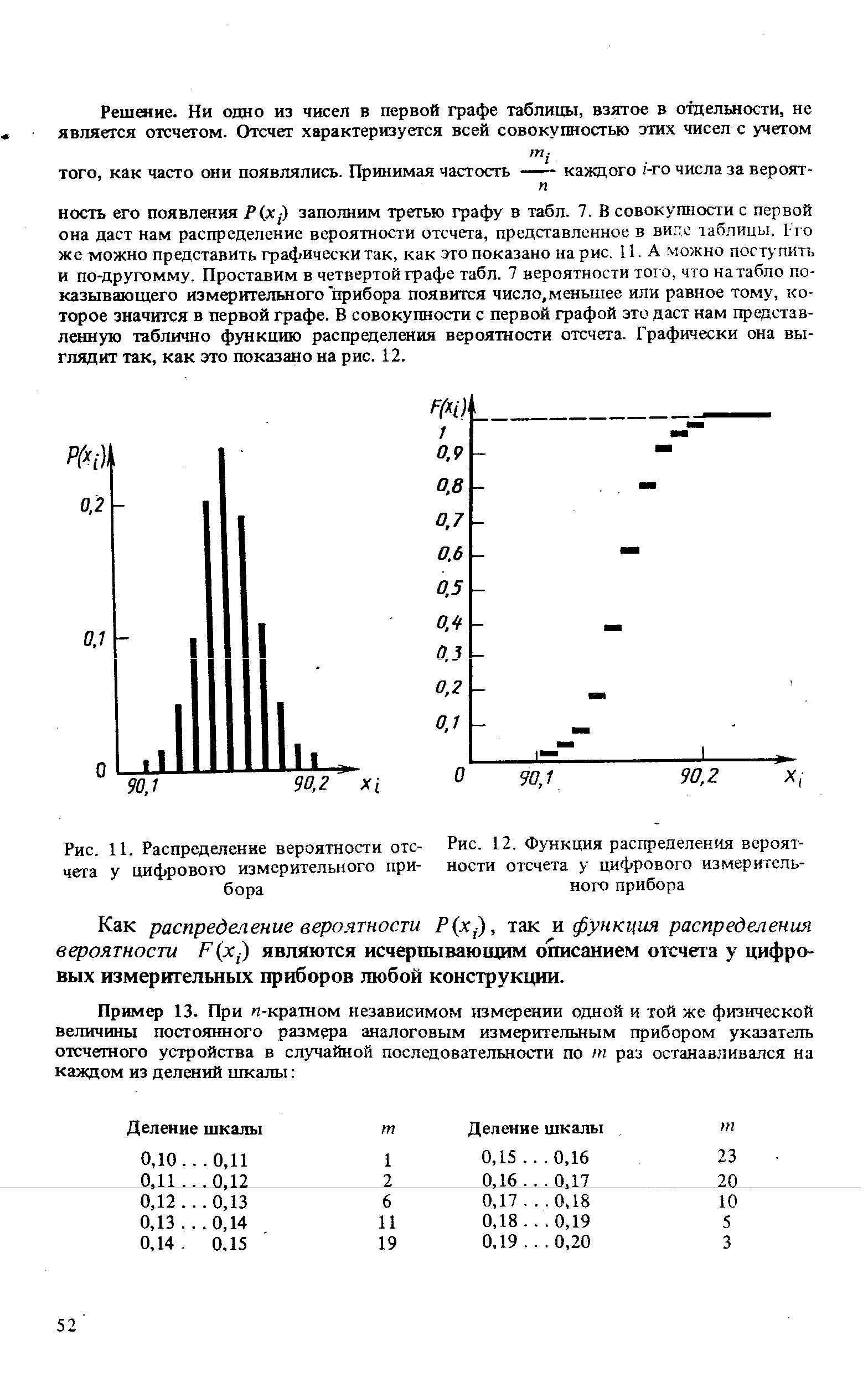 |
| Рис. 14. Кумулятивная кривая (а) и функция распределения вероятности отсчета (б) у аналогового измерительного прибора | 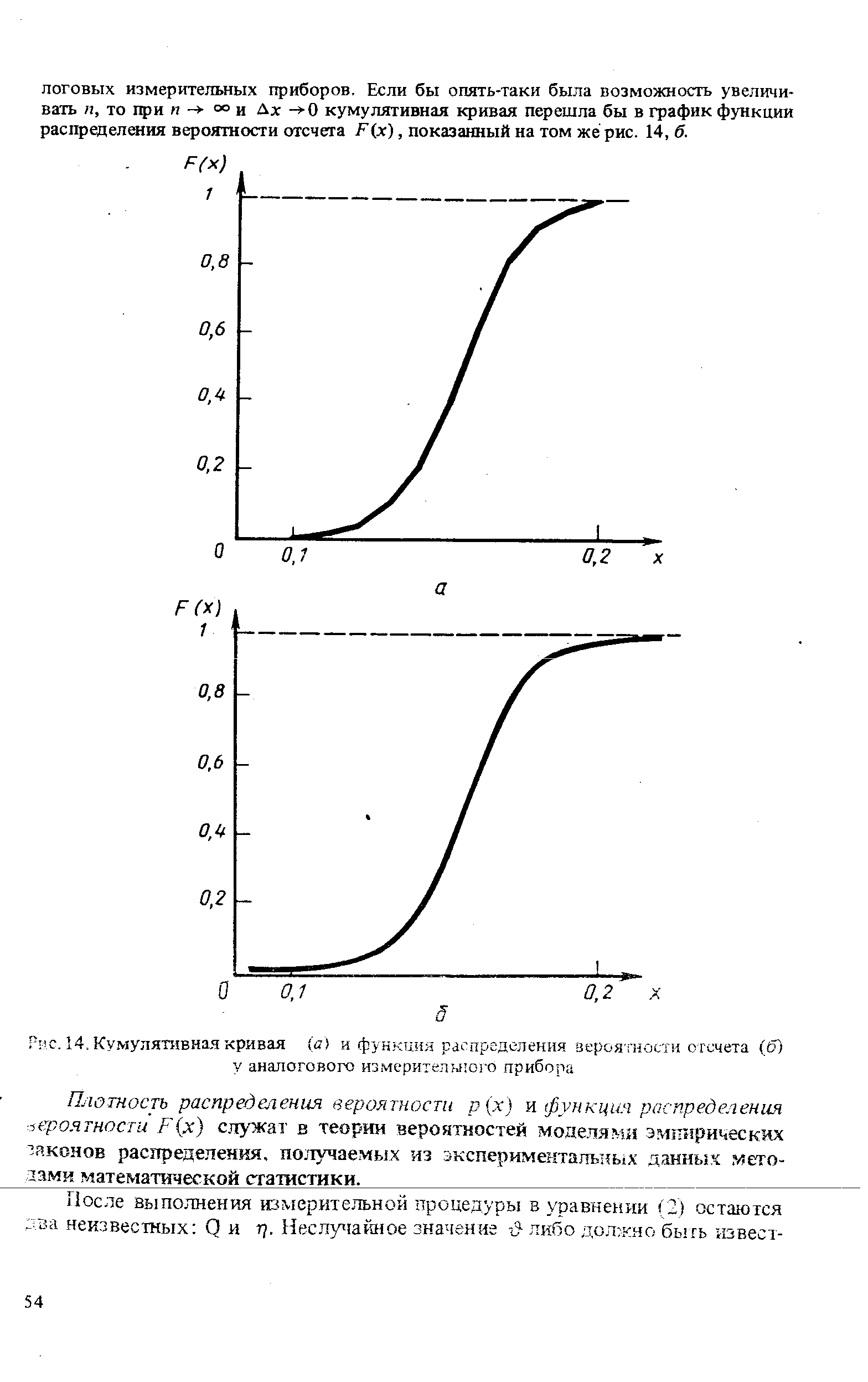 |
Геометрическая интерпретация этой операции показана на рис. 15, a F(.x0) иногда называют интегральной функцией распределения вероятности. [c.58]
Четвертый центральный момент используется для оценки заостренности дифференциальной функции распределения вероятности. Мерой заостренности служит эксцесс [c.61]
Модели эмпирических законов распределения вероятности отсчета — дифференциальная и интегральная функции распределения вероятности, как и все без исключения моменты, обладают важным качеством будучи характеристиками случайного числа, сами они не являются случайными. Описание с их помощью отсчета или результата измерения было бы очень удобным, если бы эти характеристики можно было получить. Но на практике это невозможно, так как измерительная процедура по формулам (2), (7) не может быть повторена бесконечное число раз. Поэтому и в дальнейшем они будут использоваться только в качестве моделей. [c.62]
| Рис. 42. Интегральная функция распределения вероятности К. Пирсона | 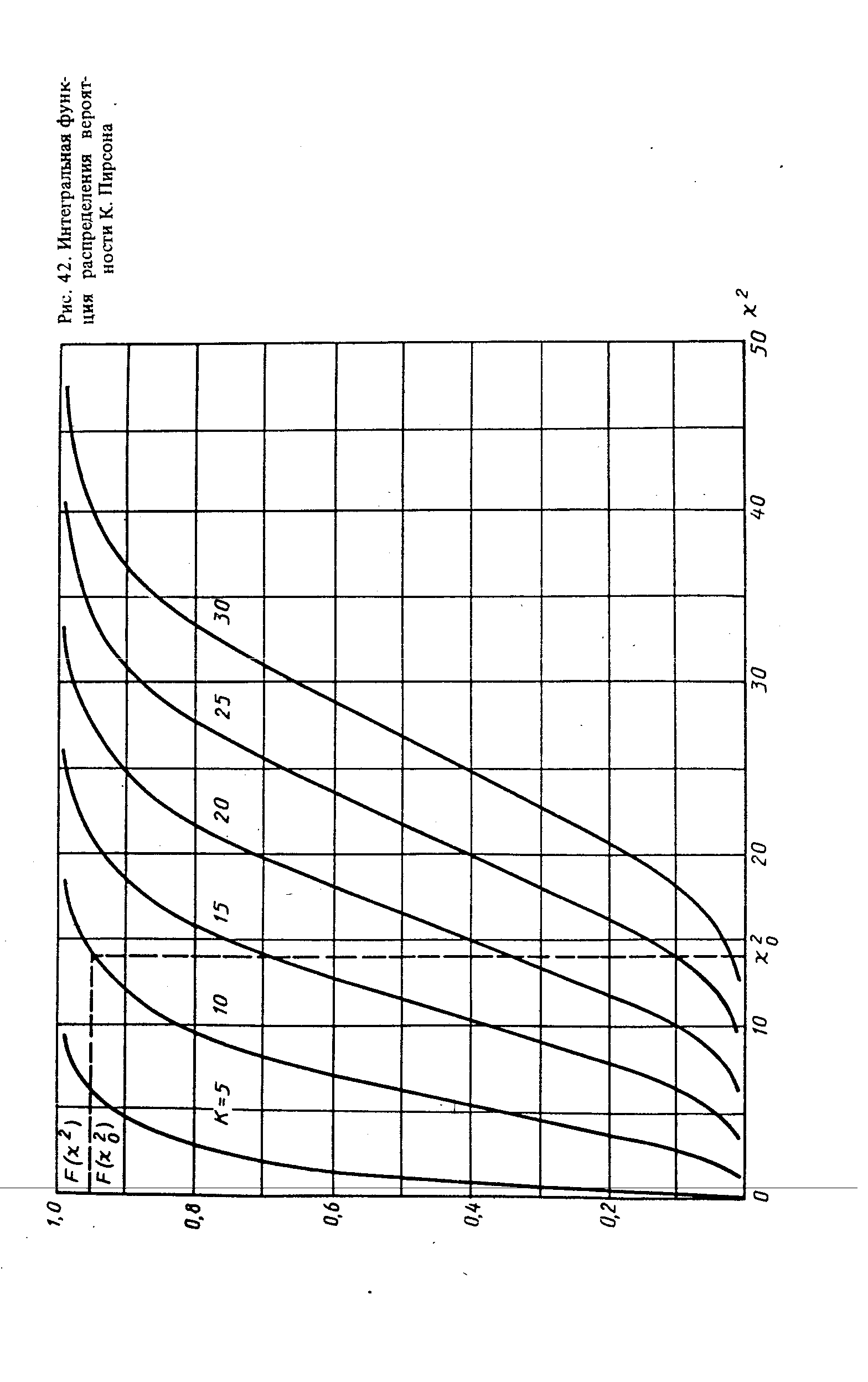 |
Плотность распределения вероятности р(х) я функция распределения вероятности F(x) служат в теории вероятностей моделями эмпирических законов распределения, получаемых из экспериментальных данных мето-дзми математической статистики. [c.54]
