| Рисунок 5.4. Кумулятивная функция нормального распределения | 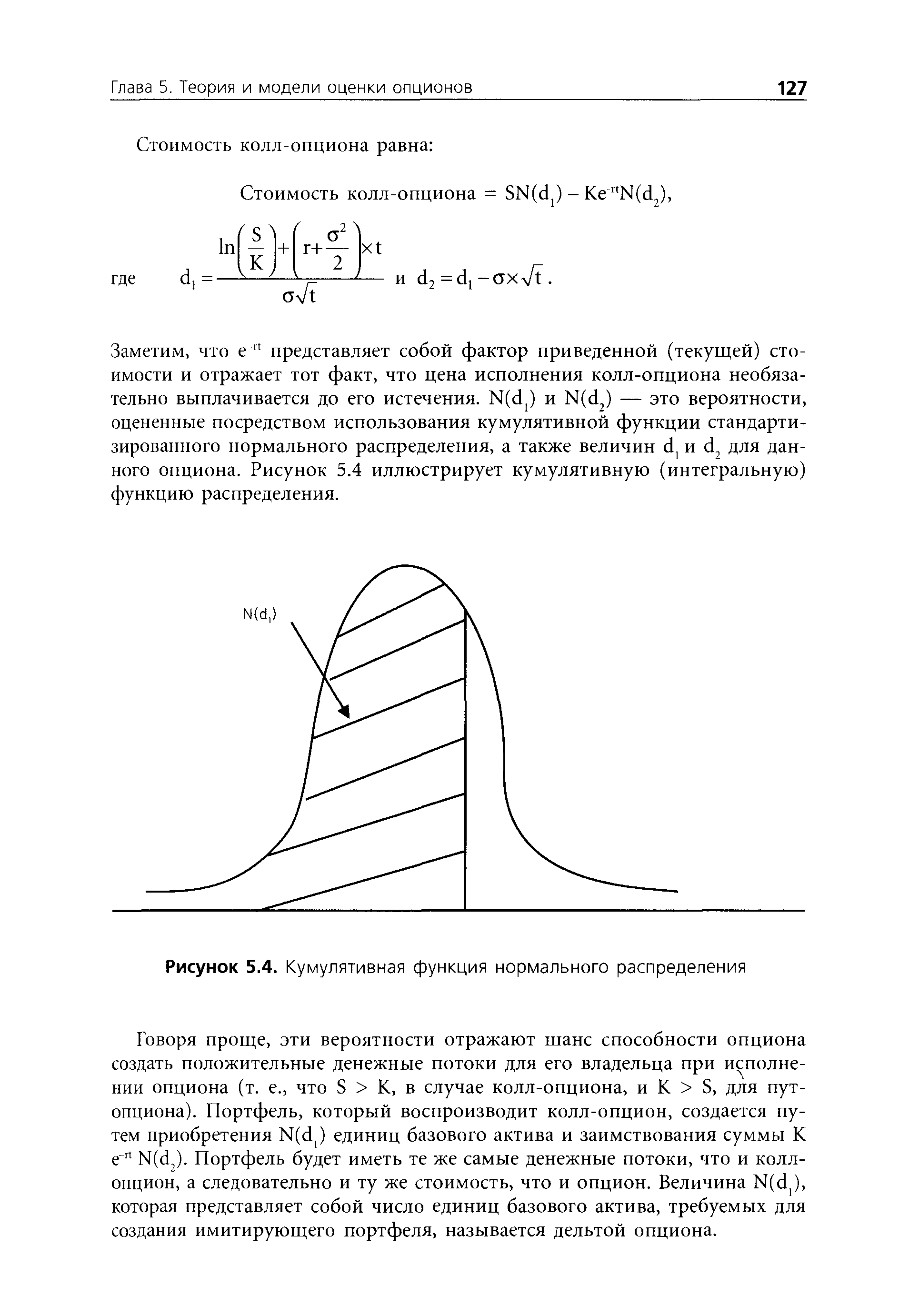 |
Кумулятивная функция нормального распределения 127 Купоны 15 [c.1301]
N(d) кумулятивная функция нормального распределения v волатильность (годовое стандартное отклонение) [c.407]
Кумулятивная функция нормального распределения может быть аппроксимирована следующим полиномом (многочленом). Во-первых, вычислите значения х , у и z . Чтобы найти N(d) d [c.407]
На следующем шаге по таблицам находятся значения кумулятивного стандартизованного нормального распределения вероятностей в точках 0,6 и 0,4. Альтернативным методом для расчета значений кумулятивного стандартного нормального распределения вероятностей является нахождение функции в виде многочлена, что было объяснено в гл. 8. [c.480]
При построении регрессионных зависимостей вид кумулятивной функции распределения F(x) не носит принципиального характера, хотя как известно [90], ввиду используемого в этом случае метода наименьших квадратов полученные оценки наилучшим образом соответствуют нормальному закону распределения. [c.155]
Заметим, что е rt представляет собой фактор приведенной (текущей) стоимости и отражает тот факт, что цена исполнения колл-опциона необязательно выплачивается до его истечения. N(dj) и N(d2) — это вероятности, оцененные посредством использования кумулятивной функции стандартизированного нормального распределения, а также величин d и d2 для данного опциона. Рисунок 5.4 иллюстрирует кумулятивную (интегральную) функцию распределения. [c.127]
Тейлор [159] изучил вопросы экономического обоснования контрольных карт кумулятивных сумм выборочного среднего для нормального распределения с известной дисперсией показателя качества. Он исходил из того, что контрольные карты кумулятивных сумм предназначаются для обнаружения разладки процесса формирования заданного показателя качества в предположении, что разладка наступает внезапно с известным смещением параметра. Ожидаемое время разладки предполагалось известным. Процесс прекращается для устранения неисправности. Если сигнал о разладке не является ошибочным, то требуется дополнительное время для обнаружения причины неполадки и ее устранения. Приближенно функция затрат основывалась на следующих допущениях [c.137]
Из стандартных таблиц функции кумулятивного распределения нормально распределенной случайной величины найдем [c.165]
N(dj) nN(d2) — кумулятивные нормальные вероятности, точнее, кумулятивные нормальные вероятности функции плотности распределения или значения накопленной вероятности для среднеквадратического распределения по d1 и d2 соответственно, т.е. с учетом стандартного отклонения акций за достаточно длительный период времени (s). [c.135]
N() = кумулятивная нормальная функция распределения вероятностей, задаваемая уравнением (3.21). [c.156]
N() = кумулятивная нормальная функция распределения вероятностей, [c.237]
Функция NORMDIST() вычисляет кумулятивное нормальное распределение и в результате получается число между нулем и единицей. Функция Р1( ) поддерживает математическую константу "тг". LN( ) есть натуральный логарифм, ЕХР( ) — экспонента аргументов, a SQRT( ) вычисляет квадратный корень. [c.210]
Позднее Гоел и By [103] опубликовали процедуру экономического обоснования контрольных карт кумулятивных сумм выборочного среднего нормально распределенного показателя качества. Авторы формулировали функцию ожидаемых затрат, следуя тем же предположениям, которые были сделаны Дунканом [88]. Ожидаемое время между первой выборкой после разладки и последней выборкой, предшествовавшей ее обнаружению, определялось с использованием результата Тейлора [159]. Определение оптимальных величин объема выборки, периода отбора выборок и параметров У-образного шаблона осуществлялось с помощью вычислительных машин. Функция затрат исследовалась численно для изучения влияния изменения параметров шаблона и некоторых параметров распределения затрат и риска на нее. [c.138]
N(d) = площадь под кривой стандартного нормального распределения или вероятность того, что при нормальном распределении со средней, равной 0, и стандартным отклонением, равным 1, результат будет соответственно меньше dl и d2 (или еще одно определение это кумулятивная нормальная вероятность функции плотности). Вычисление N(d) в Ex el производится следующим образом Функция - "НОРМРАСПР (d 0 l H THHa)". [c.65]
