Рассмотрим последовательность построения функции принадлежности на примере вещества N0 (рис. 1). На абсциссе отмечены зоны загрязнения [c.5]
Таким образом, все значения оси ординат, находящиеся в зоне менее 1 ПДК, не представляют опасности (функция принадлежности равна нулю), а в зоне более 10 ПДК - несут максимальную опасность (функция принадлежности равна единице). Интервал значений от 1 до 10 ПДК выражается линейной зависимостью. [c.6]
| Рис. 1. Определение функции принадлежности цУ° (на примере вещества N0) | 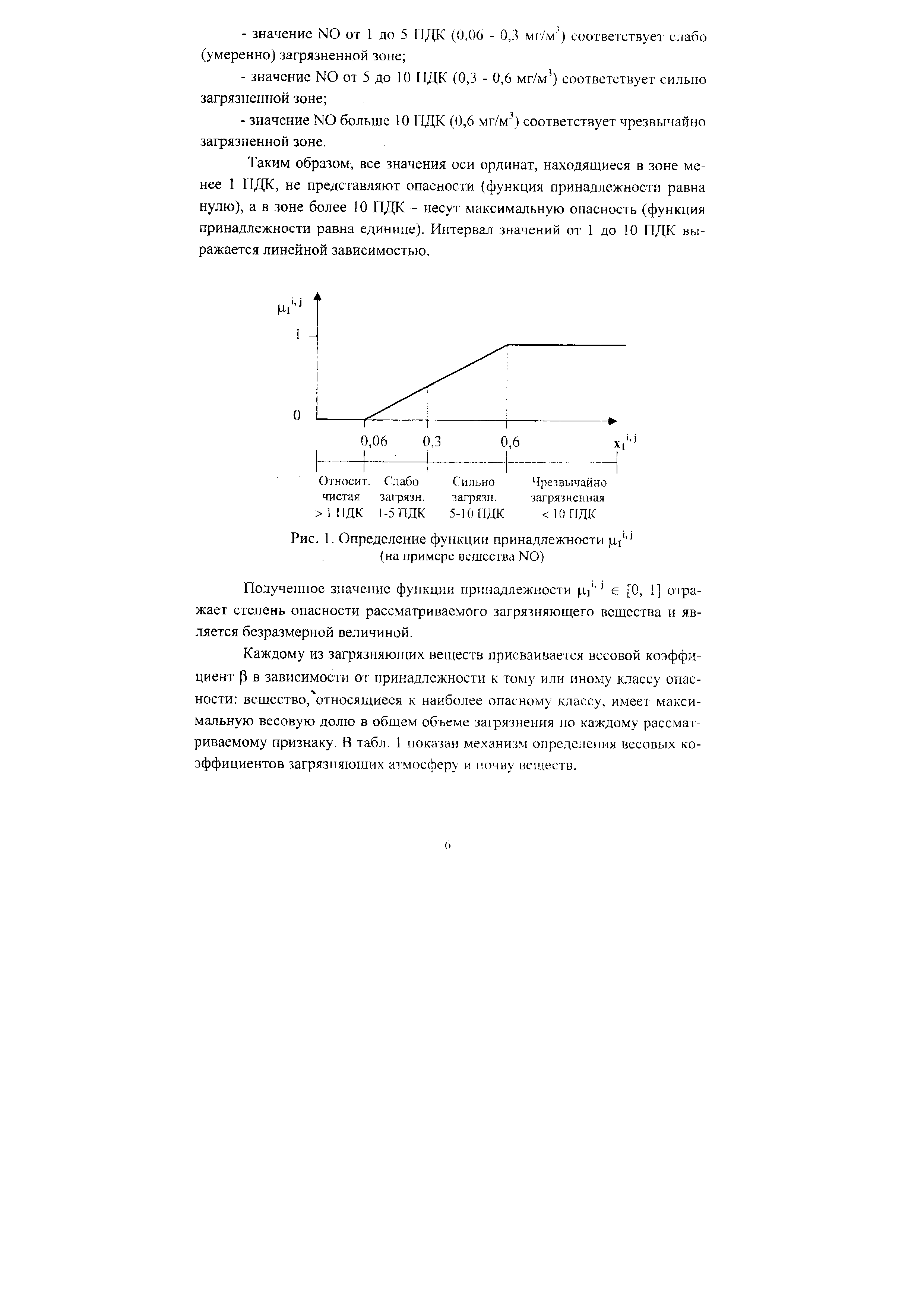 |
По набору значений м Д 1=1...1с, ] 1...т , нужно получить показатель и,], характеризующий обобщенный показатель загрязненности р-той территориальной зоны по признаку Р. Предлагается следующая свертка полученных функций принадлежности [c.7]
Ц]1 1, Ц]2 1,. .., цД - функция принадлежности или относительный показатель степени загрязнения Р/, Р 2,. ... РД соответственно порядковый номер территориальной зоны. [c.7]
Применяя аналогичную процедуру но отношению ко всем признакам РР, р=2...п, 1=1...к , получаем совокупность функций принадлежностей Цр1, 1=1...1с, р=1...п , цр 6 [О, 1]. Очевидно, чем больше значение [c.7]
В настоящей работе предлагается следующая свертка полученных функций принадлежности [c.8]
В рамках предлагаемой методики ранжирования территории по комплексному показателю качества окружающей среды могут быть использованы классические подходы к оценке воздействия суммы загрязняющих веществ на реципиента. В таком случае, расчет обобщенного показателя и,Р в шаге 1 несколько изменяется вместо построения функции принадлежности (.1Р ] по каждому значению хр , 1=1. ..1С,]=1. ..т, р=]. ..п рассчитывается суммарный показатель р-того вида загрязнения по известным в научно-технической литературе формулам. Например, химическое загрязнение атмосферного воздуха оценивается с помощью индекса загрязнения атмосферы посредством выполнения двух основных операций [39] [c.10]
Далее, аналогично шагу 1 для каждого рассчитанного классическим способом суммарного показателя 2р, стройся функция принадлежности цр, где р обозначает что эта функция принадлежности строится для Рр, а индекс 1 - порядковый номер территориальной зоны. [c.11]
Полученное значение функции принадлежности цр 6 [О, 1] отражает степень загрязнения рассматриваемого признака Рр, является величиной безразмерной. [c.11]
Для каждого из загрязняющих веществ на основе нормативных данных, была построена функция принадлежности и.щид > 1 1...18, ]=1. ..4 , характеризующая степень его опасности, где индекс I обозначает порядковый номер территориальной зоны, а]- порядковый номер загрязняющего вещества (табл. 7). [c.29]
| Рис. 6. Определение функции принадлежности .ши | 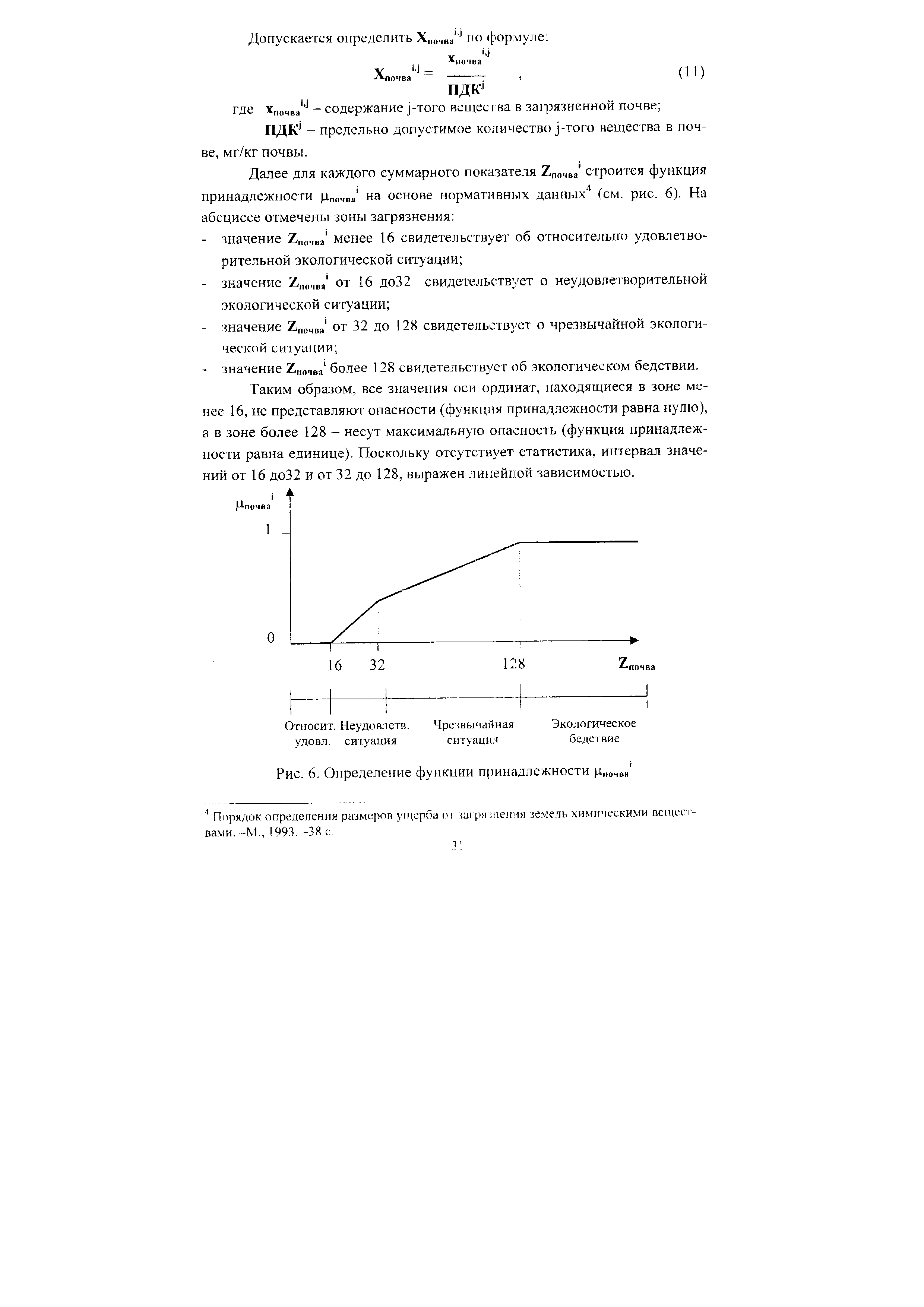 |
Формализация описания качества показателей нижнего уровня с помощью лингвистических переменных. Для построения функций принадлежности привлекаются эксперты [9]. Лингвистическая переменная характеризуется набором параметров Р, Т, X, G, М, где (3 -наименование лингвистической переменной Т - множество ее значений (терм-множество) G - семантическая процедура, позволяющая оперировать элементами терм-множества X - область определения М -семантическая процедура, позволяющая превратить каждое новое значение лингвистической переменной, образуемое процедурой G, в новое значение. [c.263]
Нечеткое описание. Такая форма описания неопределенности используется, когда информация о параметрах модели и требованиях к исследуемому объекту задается экспертом на естественном языке, то есть, в "нечетких", с точки зрения математики, терминах типа "много больше", "около", "приблизительно" и пр. Во всех этих случаях задается неточное значение параметра, а некоторое множество его возможных значений, характеризующихся уровнем компетенции эксперта. Для описания факторов в данной ситуации используют методы теории нечетких множеств, основной характеристикой которых является функция принадлежности jUj(z) параметра z к известному множеству А, удовлетворяющая условию [c.47]
После введения в рассмотрение функций принадлежности осуществляется свертка критериев по формуле [c.203]
Таким образом, каждому j-ому участку трубопровода поставлено в соответствие число ij, заключенное между 0 и 1, и чем ближе к 1 это число, тем наиболее опасен данный участок трубопровода (это следует из построения функций принадлежности и конкретного вида свертки). [c.203]
Этап 2. Решением задачи (1) будем считать некоторое нечеткое подмножество множества заданных альтернатив, функция принадлежности для элементов которого вычисляется с помощью монотонной агрегирующей функции [c.99]
Изначально функция принадлежности имела вид nj(fj(xj)), но т.к. f зависит только от X, то ее сократили. [c.105]
Подставив значения параметров, найдем значения функций принадлежности и - по формуле средней геометрической - агрегирующей функции принадлежности (табл. 9). [c.110]
Коэффициенты функций принадлежности. [c.112]
Значения функции принадлежности и агрегирующей функции принадлежности. [c.113]
Агрегирующая функция принадлежности 0,354 0,743 0,256 0,363 [c.113]
Тогда функции принадлежности нечетких множеств у, (1=1,3), описывающие нечеткие цели и ограничения (3.5), будут иметь вид [c.48]
Нечеткое множество А в полном множестве области рассуждений U характеризуется функцией принадлежности FA U —> [О, 1], которая каждому элементу у множества U ставит в соответствие число FA (у) из отрезка [О, 1], описывающее степень принадлежности элемента у множеству А. [c.29]
Треугольному нечеткому числу N, заданному таким образом, соответствует нечеткое множество A (N), функция принадлежности которого определена на множестве [c.29]
Данная функция принадлежности имеет вид треугольника с вершинами в точках с координатами (о - сь 0) (а, 1) (а + сг, 0). [c.30]
В основе данной теории лежат понятия нечеткого множества и функции принадлежности, определение которых приводятся ниже. [c.184]
Пусть Е — множество, счетное или нет, и х — элемент Е. Тогда нечеткое подмножество А множества Е определяется как множество упорядоченных пар (х, ц%(х)) , Vx E, где Из(х)—характеристическая функция принадлежности, принимающая свои значения во вполне упорядоченном множестве М, указывающая степень принадлежности элемента д подмножеству А. Множество М называется множеством принадлежностей. [c.185]
Пусть Л X х Y -> [О, 1] — функция принадлежности нечеткого бинарного отношения R, определяемая с помощью эксперта. [c.186]
Для этого следует, определив функцию принадлежности предлагаемого товара х +, , провести счет согласно приведенному алгоритму, и определить, в какой степени этот товар принадлежит множеству товаров перспективного ассортимента, а если принадлежит, то не вытеснит ли он каких-либо товаров из набора хг. . . , хп, уже находящихся на складе предприятия оптовой торговли. [c.190]
В основе данной теории лежат понятия нечеткое множество и функция принадлежности . [c.79]
Далее для каждого суммарного показателя 2ПОЧВ., строится функция принадлежности и чва на основе нормативных данных4 (см. рис. 6). На абсциссе отмечены зоны загрязнения [c.31]
Выберем 9 количественных параметров. Для определения функций принадлежности для каждого из них найдем значения параметров, соответствующие узловым точкам функциям принадлежности. Характеристика узловых точек и соответствующие им значения парамечров представлены в таблицах 6 и 7. [c.110]
Пусть l/s Y x Z -> [О, 1]— функция принадлежности нечеткого бинарного отношения S. Для всех у е Y и всех z e Z ijtgfy, z) равна степени совместимости розничного торгового предприятия z с признаком у. Чем выше значения функции, тем более данный признак совместим с конкретным предприятием розничной торговли. [c.186]
Смотреть страницы где упоминается термин Функция принадлежности
: [c.207] [c.207] [c.8] [c.130] [c.383] [c.203] [c.99] [c.99] [c.105] [c.106] [c.106] [c.187]Смотреть главы в:
Нечетко-множественный анализ риска фондовых инвестиций -> Функция принадлежности
Фондовый менеджмент в расплывчатых условиях -> Функция принадлежности
