Треугольному нечеткому числу N, заданному таким образом, соответствует нечеткое множество A (N), функция принадлежности которого определена на множестве [c.29]
Определим нечеткие числа в [0,1], как треугольные нечеткие числа (а, с/, сг), где а — центр, с( и сг — величины нечеткостей слева и справа. [c.31]
Треугольные нечеткие числа [c.31]
| Рис. 2.3. Функция принадлежности треугольного нечеткого числа | 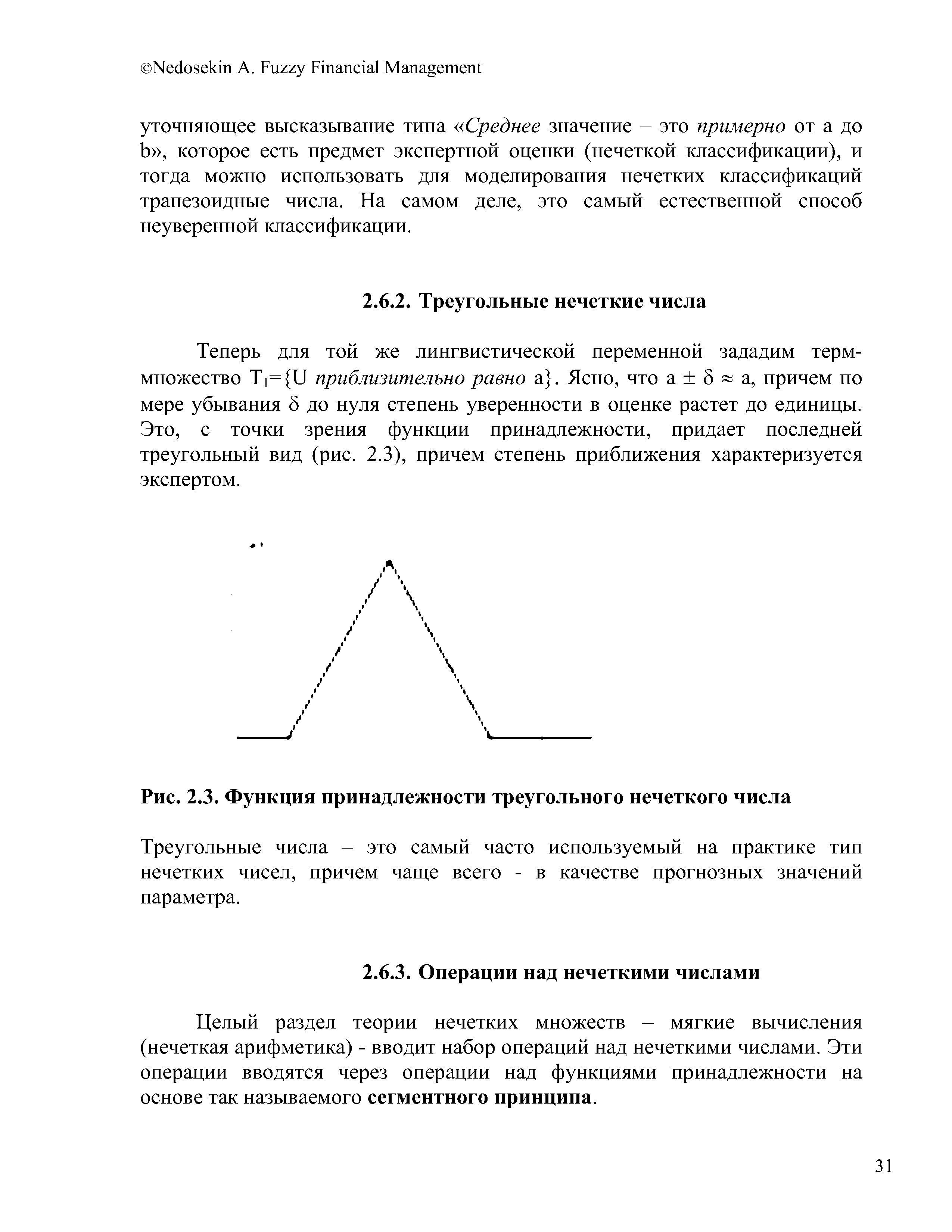 |
Тогда треугольное нечеткое число будет иметь вид (650,670,675). [c.55]
Если все параметры в (4.1) обладают "размытостью", т.е. их точное планируемое значение неизвестно, тогда в качестве исходных данных уместно использовать треугольные нечеткие числа с функцией принадлежности следующего вида (рис. 4.1). Эти числа моделируют высказывание следующего вида "параметр А приблизительно равен а и однозначно находится в диапазоне [ат п, ап [c.70]
И если получена обоснованная оценка транзитного коэффициента корреляции, например, в форме треугольного нечеткого числа, то задача синтеза оптимальной опционной комбинации решается модифицированным методом Марковица. [c.139]
Все постоянные коэффициенты в (3.16) - (3.17) являются треугольными нечеткими числами. Можно было бы как-то отличить треугольные параметры от обычных скалярных, вводя специальную запись, но, честно говоря, мне не хочется загромождать формулы. И, поскольку в нашем случае О2 Оь то имеет место приближенное равенство [c.85]
П1.6.2. Треугольные нечеткие числа [c.156]
Дно тренда - выраженный локальный или глобальный минимум индекса. Обычно дно ищется в форме треугольного нечеткого числа. [c.196]
| Рис. 1.10. Треугольное нечеткое число | 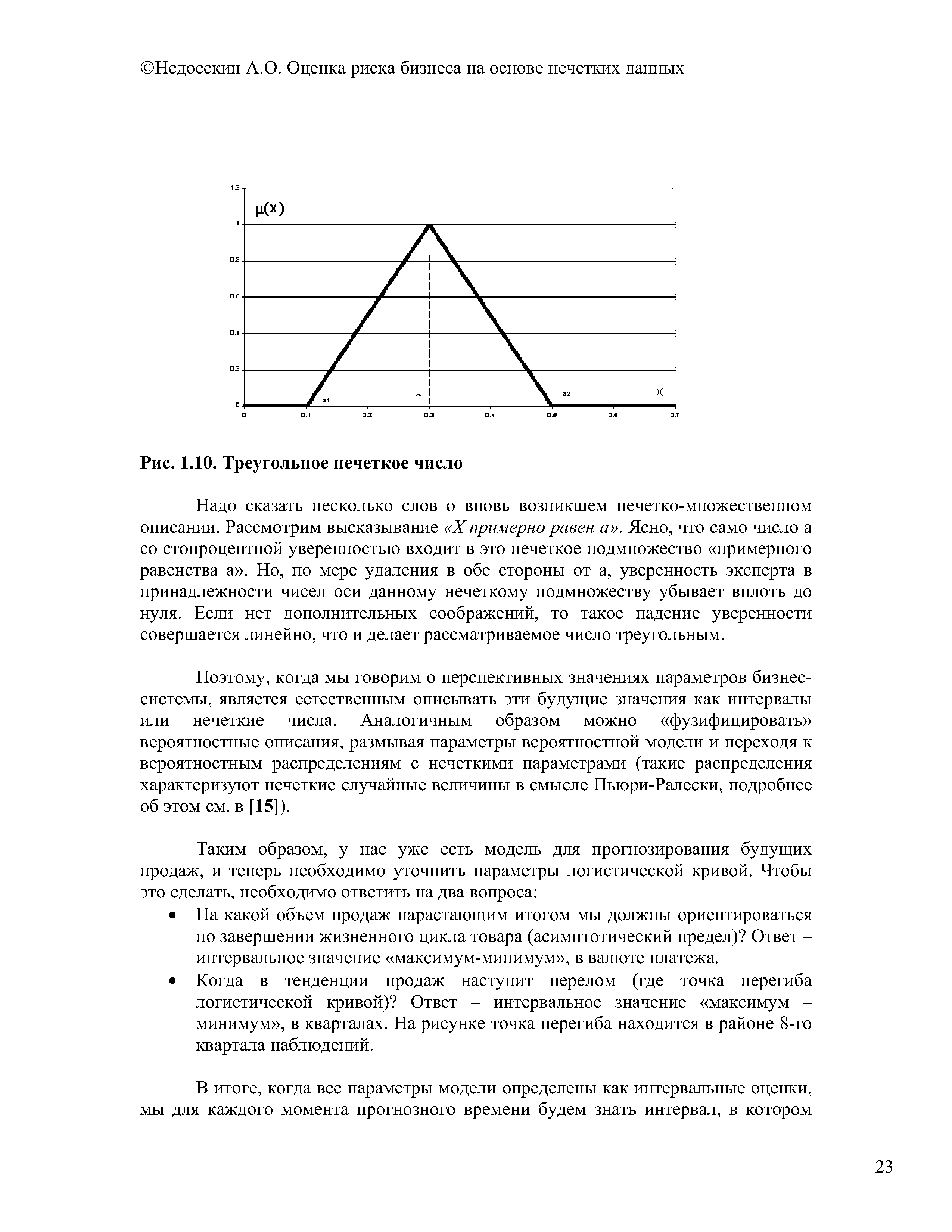 |
Впервые представление чистой современной ценности проекта в форме треугольного нечеткого числа встречается в [31]. [c.54]
Задавшись приемлемым уровнем дискретизации на интервале принадлежности [0,1], можно реконструировать результирующее нечеткое число МРУ (ЧДД) путем аппроксимации его функции принадлежности ломаной кривой по интервальным точкам. Часто оказывается возможным привести NPV к треугольному виду, ограничиваясь расчетами по значимым точкам нечетких чисел исходных данных. Это позволяет рассчитывать все ключевые параметры в оценке степени риска не приближенно, а на основе аналитических соотношений. [c.19]
Для каждой из групп получаем неопределенное число (не треугольное), графическое представление которого показано на рис. 9.7. Решение заключается в том, чтобы принять в качестве результата (стоимости капитала) нечеткое число, образованное наиболее близкой к началу координат стороной в качестве нижней границы и наиболее отдаленной стороной—в качестве верхней. [c.140]
Тогда мы можем рассматривать числа (xib xiL, xi2) как треугольные нечеткие параметры плотности распределения, которая и сама в этом случае имеет вид нечеткой функции. А зона предельного правдоподобия тогда есть не что иное, как нечеткий вектор. [c.37]
Полученное описание позволяет разработчику инвестиционного проекта взять в качестве исходной информации интервал параметра [атщ, атах] и наиболее ожидаемое значение а, и тогда соответствующее треугольное число А= (a n, a, amax) построено. Далее будем называть параметры (атщ, а, атах) значимыми точками треугольного нечеткого числа А. Вообще говоря, выделение трех значимых точек исходных данных весьма распространено в инвестиционном анализе (см., например, [4.8, 4.9]). Часто этим точкам сопоставляются субъективные вероятности реализации соответствующих ("пессимистического", "нормального" и "оптимистического") сценариев исходных данных. Но мы не считаем себя вправе оперировать вероятностями, значений которых не можем ни определить, ни назначить (в главе 1 настоящей работы мы коснулись этого предмета, в частности, говоря о принципе максимума энтропии). Поэтому в инвестиционном анализе мы замещаем понятие случайности понятиями ожидаемости и возможности. [c.70]
Как подробно рассмотрено в главе 5 работы, цена подлежащего актива может моделироваться винеровским случайным процессом лишь при определенных оговорках. Реальная статистика бумаг по существу является квазистатистикой, поскольку бумага торгуется на рынках с изменяющимися условиями, и, следовательно, статистической однородности нет. Однако можно сохранить допущение о нормальном распределении цены актива, оговорившись, что в этом распределении параметры являются треугольными нечеткими числами. [c.109]
В процессе изложения математических соотношений будем применять следующие обозначения. Точка после символа (А ) означает, что рассматривается треугольное нечеткое число или нечеткая функция (последовательность). Во всех прочих случаях по умолчанию предполагаются действительные числа, функции, параметры. Для треугольного числа A Amin, Aav, Amax - минимальное, среднее и максимальное значения числа. [c.115]
Z - коэффициент приведения расчетной доходности инедса акций первого эшелона к тому же для второго эшелона - треугольное нечеткое число [c.116]
По результатам формирования семантической модели предметной области, с выделением всех необходимых сущностей и связей между ними, ИЗ переходит к процессному описанию связи параметров. Но сначала он должен согласовать с экспертом нечеткую грануляцию уровней параметра при задании соответствующей лингвистической переменной. Например, в контроллере Мамдани заложена следующая нечеткая грануляция носителя лингвистической переменной Уровень комнатной температуры (рис. 1.5), базирующаяся на трапециевидных и треугольных нечетких числах. Соответствующее описание в структуре образца [c.25]
Треугольное нечеткое число А = (Am n, Aav, Amax) может быть интерпретировано как интервальная оценка параметра, содержащая минимальное, наиболее ожидаемое и максимальное значения параметра. Соответственно, последовательность треугольных нечетких чисел - это множество треугольных чисел со своими интервальными оценками мощностью N, где N - число интервалов финансового планирования. Все нечеткие числа мы выделяем в данной главе шрифтом Bold, а обычные действительные числа оставляем без выделения. [c.47]
Все арифметические операции с треугольными нечеткими числами подчиняются правилам мягких вычислений, о чем подробно см. в [35]. Результат мягких вычислений, что мы оговариваем особо, может быть трианглизирован (приведен к виду треугольного нечеткого числа). Такое допущение справедливо во всех случаях реального бизнес-планирования и выполняется точно для операций мягкого сложения и вычитания. Если же трианглизация невозможна, то оценку риска инвестиционного проекта можно произвести приближенно, о чем говорится в самом конце статьи. [c.47]
То же и с треугольными нечеткими числами мы говорим, что ожидаемый результат группируется вокруг ожидаемого среднего и не выходит за некоторые пределы. Нам не надо напрягаться, чтобы вводить вероятностное распределение, матожидание, дисперсию и т.д. Все это, в условиях дефицита информации, выглядит как искусственное безосновное построение. Когда мы вводим нечеткие описания, мы естественным образом моделируем ими свои ожидания а вероятность в этом процессе выглядит как назойливый посредник. [c.98]
Анализируя свойства нелинейных операций с нечеткими числами (например, деления), исследователи приходят к выводу, что форма функций принадлежности результирующих нечетких чисел часто близка к треугольной. Это прозволяет аппроксимировать результат, приводя его к треугольному виду. И, если приводимость налицо, тогда операции с треугольными числами сводятся к операциям с абсциссами вершин их функций принадлежности. [c.34]
Например [2.3], прогноз продаж компании (нарастающим итогом) задан тремя функциями вещественной переменной fi(T) - оптимистичный прогноз, f2(T) -пессимистичный прогноз, fs(T) — среднеожидаемые значения продаж, где Т — время прогноза. Тогда лингвистическая переменная Прогноз продаж в момент Т есть треугольное число ( fi(T), f2(T), fs(T) ), а все прогнозное поле есть треугольная нечеткая функция (рис. 2.5), имеющая вид криволинейной полосы. [c.35]
Смотреть страницы где упоминается термин Треугольные нечеткие числа
: [c.66] [c.67] [c.77] [c.88] [c.90] [c.135] [c.159] [c.159] [c.178] [c.34] [c.134] [c.139] [c.29] [c.33] [c.91] [c.103] [c.115] [c.158]Смотреть главы в:
Нечетко-множественный анализ риска фондовых инвестиций -> Треугольные нечеткие числа
