Полное время ремонта определяется, в частности, организацией рабочего цикла. Чистая длительность собственно ремонта в обычно используемых методиках предполагается распределенной показательно, однако современное состояние теории очередей позволяет рассчитывать временные задержки при более общих допущениях — см. главу 3. Особо подчеркнем необходимость и возможность представления ремонтных органов высших звеньев как сетей обслуживания. [c.260]
В 70-е годы революционная власть, трезво оценивая запущенное состояние сельского хозяйства, сосредоточилась на мерах по распределению среди малоимущих крестьян земель, конфискованных у королевской семьи и высших чиновников старого режима, изъятых у итальянских колонистов, а также у местных феодалов и родо-племенной аристократии. Каких-либо строгих норм землепользования в Ливии правительство не устанавливав ло, поскольку стремилось вовлечь максимум площади в сельскохозяйственный оборот и занять в отрасли как можно больше людей. Была лишь закреплена законодательно общественная собственность на землю, которая юридически перестала быть товаром. В то же время на рубеже 70—80-х годов около 60% обрабатываемых сельскохозяйственных угодий находилось в частном пользовании (в том числе до 35% сосредоточивали средние и ряд крупных индивидуальных фермерских хозяйств капиталистического типа, широко применявшие преимущественно иностранную рабочую силу и составлявшие пятую часть всех предприятий отрасли, и примерно 25%—мелкотоварные, в основном кооперированные, фермы), свыше 28% сохранилось за общинами, и лишь менее 12% земельных площадей занимали собственно государственные хозяйства и опытно-показательные фермы (рассчитано по [95, с. 1 168, с. 102—104]). [c.165]
Закон распределения случайной величины, обладающей следующим свойством промежутки времени между любыми двумя соседними событиями и его среднее квадратическое отклонение равны 1/Х, где — интенсивность потока, являющегося экспоненциальным, или показательным. [c.177]
Непрерывная случайная величина X имеет показательный (экспоненциальный) закон распределения с параметром Я,, если ее плотность вероятности имеет вид [c.34]
| Таблица 9. Эмпирические и выравненные по показательной кривой частоты распределения времени пролеживания детали пакет ротора изделия IV в переходящем заделе |  |
| Рис. 14. Гистограмма распределения времени пролеживания на складе деталей и выравнивающая ее показательная кривая. | 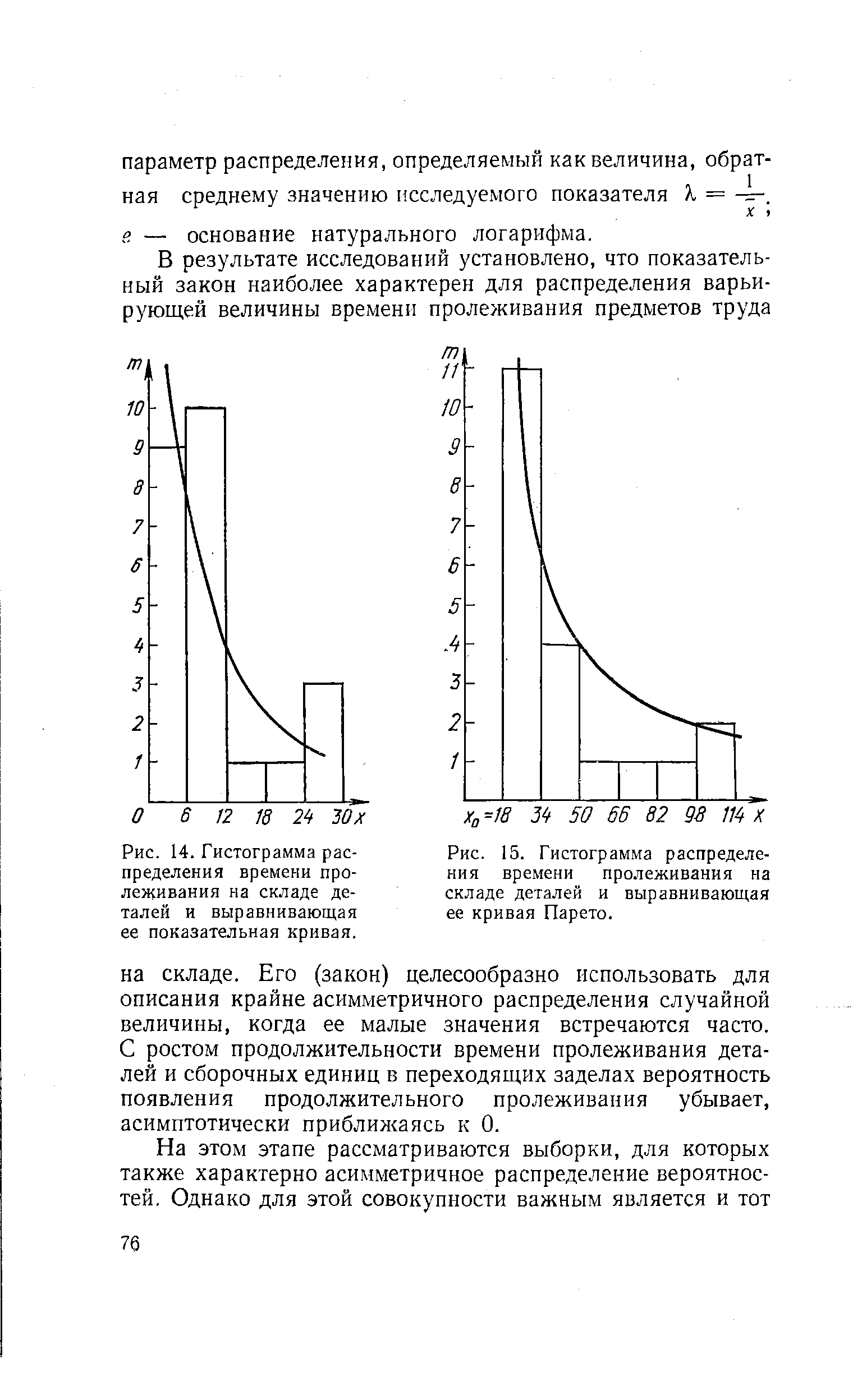 |
В случаях, когда кривые распределения времени пролеживания деталей и сборочных единиц в переходящих заделах описываются функциями, отличными от показательного закона, необходимо использовать соответствующие им интегральные функции накопленных вероятностей. [c.79]
| Рис. 22. Функция распределения вероятности квадрата скорости жидкости, нормализованная к ее среднему времени, в одиннадцатом слое игровой модели гидродинамической турбулентности, обсуждаемой в тексте. Вертикальная ось имеет такой логарифмический масштаб, что прямая линия, которая помогает глазу, квалифицируется, как очевидное показательное распределение. Обратите внимание на появление чрезвычайно редких и больших взрывов скоростей на краю, выше экстраполяции прямой линии. Источник [252]. | ![Рис. 22. <a href="/info/21981">Функция распределения вероятности</a> квадрата скорости жидкости, нормализованная к ее среднему времени, в одиннадцатом слое игровой модели гидродинамической турбулентности, обсуждаемой в тексте. Вертикальная ось имеет такой логарифмический масштаб, что прямая линия, которая помогает глазу, квалифицируется, как очевидное показательное распределение. Обратите внимание на появление чрезвычайно редких и больших взрывов скоростей на краю, выше экстраполяции прямой линии. Источник [252].](/pic1/205196012179108108119160056012034002236089221065.png) |
Показательное распределение, обсуждавшееся в предыдущей разделе, было [c.70]
Например, для показательного распределения f(x, 0) = е вх, где 0 — неизвестный параметр, который следует оценить по выборке (xt, x2,. .., хп), составим функцию правдоподобия [c.49]
Весьма показательно распределение мирового промышленного экспорта. Доля в нем развитых стран к середине 1990-х гг. достигла 78,0%, развивающихся стран — свыше 16,0%, а бывших социалистических стран Восточной Европы и СССР — около 6,0%. [c.36]
Время обслуживания автомобилей укрупненной комплексной бригадой подчинено показательному закону с параметром к Это означает вероятность того, что время обслуживания v меньше / и равно P v
Время обслуживания автомобилей укрупненной комплексной бригадой подчинено показательному закону с параметром и. Это означает вероятность того, что время обслуживания и меньше t и равно P(v < /), где Д/) — функция распределения времени обслуживания 1/и — математическое ожидание времени обслуживания. [c.272]
О - параметр обслуживания, который в случае показательного распределения равен величине, обратной среднему времени обслуживания. [c.168]
Особенности поведения предприятия, связанные со стохастическим и законами принятия решения в системе оптовой торговли средствами производства, можно исследовать при помощи имитационных моделей с использованием метода машинного моделирования [4]. Имитацию поведения предприятия проведем при заключении данным предприятием договоров с поставщиками и потребителями и при совершении акта продажи своей продукции. При заключении договоров предполагается, что предприятие заявило потребителям количество и номенклатуру продукции, которую ему выгодно выпускать с точки зрения максимума прибыли. С другой стороны, оно сделало заказ поставщикам на ресурсы, необходимые для этого состава и объема выпуска продукции. В процессе формирования договоров случайным является поведение поставщиков и потребителей. Предполагается, что поставщики с некоторым заданным законом распределения вероятностей принимают или не принимают заказы на ресурсы. Аналогично потребители с некоторым заданным законом распределения вероятностей принимают или не принимают заявки на заказ соответствующего вида средств производства. Причем отказ в принятии заказа или заявки на заказ может быть (в большинстве случаев будет именно так) не только полным, но и частичным. Используя способность ЭВМ формировать случайные числа, можно имитировать поведение предприятия при различной реакции внешней среды (потребителей и поставщиков). Экономически вполне оправданно считать, что вероятность величины отказа поставщиков и потребителей распределена по показательному закону. Действительно, с возрастанием величины отказа его вероятность уменьшается, причем это уменьшение происходит явно быстрее, чем по линейному закону. Задавая, кроме того, вероятность той или иной реакции данного предприятия на поведение поставщиков и потребителей при формировании договоров, можно получить приближенную картину его функционирования при разных характеристиках внешней среды и его внутренних характеристиках. Операторная схема и блок-схема моделирующего алгоритма для данной имитационной модели имеют следующий вид [c.90]
Продолжительность периодов состояний объектов подчиняется, как правило, показательному закону распределения. При среднем времени / и tb периодов рабочего, а та и ть — нерабочего состояний объектов А и В вероятность р (t) продолжительности t для любого периода определится [c.118]
При показательном распределении величин /2, t3n q с параметрами соответственно Я2, К3, Kq вероятности Р2П и Рзп определяются выражениями [c.118]
Это выражение характеризует предельное значение вероятности простоя В при состоянии системы Ха из-за недостатка запаса в С при показательном распределении q и tz и отсутствии специального страхового запаса, образование которого не связано с накоплением продукта в С вследствие перебоев в работе. [c.119]
При показательном распределении времени простоев и остатков продукта в Са и Сь, с параметрами Ка = > А,ь = —, A,t =-—, вероятность определяется выражением Р =- [c.121]
Из теоретических законов для описания статистических распределений межпоездных интервалов наибольшее применение находит распределение Эрланга. Установлено, что для предприятий с внешним прибытием до 10 млн т в год распределение межпоездных интервалов удовлетворительно описывается законом Эрланга первого порядка или показательным законом, для предприятий с внешним прибытием 10 млн. т в год и более — по закону Эрланга второго порядка. [c.56]
Рассмотрим решение такой задачи в условиях Нефтекум-ского УБР. Анализ работы службы испытания позволил составить статистические ряды интенсивности сдачи скважин на испытание и продолжительности испытания. Изучение рядов позволило сделать вывод, что поток скважин, поступающих в испытание, является одинарным стационарным потоком без последствия, т. е. обладает свойствами пуассоновского потока. С достаточной степенью точности можно допустить, что время обслуживания распределяется по показательному закону. На основании статистических рядов составлены таблицы распределения интенсивности сдачи скважин на испытание (табл. 36) [c.68]
Анализ функционирования СМО. Рассмотрим наиболее общий случай СМО, когда п - канальная система работает в режиме с ожиданием обслуживания и с ограничением на длину очереди (в очереди не может быть более т требований). Предполагается, что входящий поток требований описывается пуассо-новским законом распределения с интенсивностью X, а время обслуживания требований распределено по показательному закону с интенсивностью ц. [c.67]
Для статистического выявления относительной роли различных факторов квалификации в области конторского труда мы воспользовались данными карточек-формуляров по двум крупным московским учреждениям — Наркомпроду и Московскому почтамту, где эти формуляры заполнялись более тщательно, чем в других местах. Выбор этих учреждений диктовался еще тем соображением, что здесь мы имели дело с такими приложениями конторского труда — в области службы связи и распределения, — общественная необходимость которых вне всякого спора. Повышение продуктивности труда в этой области способно принимать особенно осязательные для нас формы. И роль образования, повышающего количественно и качественно успешность такого рода труда, выявляется здесь наиболее наглядно ж показательно. [c.114]
Изучение статистических материалов дает основание предполагать, что распределение продолжительности интервалов между моментами поступления (выбытия) партий нефтепродуктов в ре-зервуарные емкости пункта перевалки близко к показательному закону распределения. [c.110]
Перед тем, как вернуться к данным, мы должны спросить себя о том, что можно ожидать на основе гипотезы случайных блужданий. Если ценовые изменения независимы, положительные (+) и отрицательные (-) шаги следуют друг за другом подобно "орлам" и "решкам" рыночного броска монеты. Для симметричных распределений ценовых изменений, начинающихся с плюса, +, вероятность получить минус, -, равна 1/2. Вероятность получить два минуса в ряду -1/2x1/2=1/4 вероятность получить три минуса в ряду - 1/2 х 1/2 х 1/2 = 1/8, и так далее. Для каждого дополнительного отрицательного приращения мы видим, что вероятность делится надвое. Это определяет так называемое экспоненциальное распределение, описывающее тот фаю1, что увеличение длительности просадки на одну единицу времени делает ее вдвойне менее вероятной. Этот показательный закон также известен, как закон Пуассона и описывает процессы, не имеющие [c.67]
Поскольку, в случайной модели без памяти, существует больше половины просадок с продолжительностью большей, чем один временной период, то удобно визуализировать эмпирическое распределение этих просадок на рынке акций в логарифмическом масштабе, где ожидаемое показательное распределение становится прямой линией. Это весьма эффективный метод проверить действительность гипотезы отклонения от прямой линии будут сигнализировать некоторое отклонение от показательного распределения и, таким образом, от гипотезы об отсутствии памяти. [c.67]
Перед отклонением нашей начальной гипотезы и принятием идеи, что рыночные цены - не полностью случайны, мы должны, во-первых, проверить, что наблюдение "статистически значимо". Проще говоря, это означает, что отклонение от экспоненты могло быть результатом малости набора данных или других, не идентифицированных факторов, не связанных с данными. Очевидное отклонение от показательного распределения не было бы, в этом случае подлинным, а явилось бы следствием ошибки, артефактом наших измерений или просто случайностью. Чтобы попытаться избежать этих ловушек, мы, нуждаемся в тестах, которые сообщают нам о том, что наблюдаемое отклонение существенно и заслуживает доверия. Действительно, бритва Оккама говорит, что мы должны предпочесть более простую гипотезу о случайности, пока сила очевидности не заставит изменить наши убеждения. [c.76]
Чтобы посмотреть, какое из этих двух описаний (случайное или неслучайное) является наиболее точным, был выполнен следующий статистический анализ рыночных колебаний. Во-первых, мы аппроксимировали распределение просадок, меньших 15% для DJIA показательным распределением и нашли характеристический 2% масштаб спада. Эта характеристическая константа затухания означает, что вероятность наблюдения спада, большего 2% - приблизительно 37%. Следуя нулевой гипотезе о том, что экспоненциальное описание является правильным, и, экстраполируя это описание, например, на три самых больших краха на американском рынке в этом столетии (1914, 1929, и 1987), как показано на Рис. 24, получаем время повторения для каждого отдельного краха равным, приблизительно пятидесяти столетиям. В действительности, три краха произошли в одном столетии. Этот результат - первый признак того, что показательная модель не применима к большим крахам. [c.77]
Рискдосрочиого возмещения основного капитала по ипотекам может быть распределен среди различных траншей, однако в целом снизить его невозможно. Хотя держатели краткосрочных траншей подвергаются меньшему риску предоплаты, тем не менее при резком падении процентных ставок им может быть выплачена номинальная стоимость гораздо раньше срока, что окажет негативное влияние на их инвестиции. Оценка риска предоплаты — чрезвычайно сложная задача, особенно когда речь идет о более сложных формах СМ О, которые могут состоять из различных комбинаций таких специфических бумаг, как классы планового погашения долга в рассрочку (РАС), компаньонские транши, первоклассные ценные бумаги и транши Z o скачком. Несмотря на это, появление СМО - показательный пример того, как финансовые рынки реагируют на нужды обладателей и пользователей капитала, создавая новые, гибкие по своей структуре ценные бумаги. [c.396]
Другой показательный пример распределения ролей участни- [c.103]
Идеология классической политической экономии господствовала длительное время, идеология, которая этическую точку зрения делала излишней, поскольку она предполагала, что механизм экономической жизни производит собственной силой тоу что этика ожидает от осуществления своих идеалов, В этом плане показательно высказывание французского экономиста, представителя классической политической экономии Ф. Бастиа (1801—1850). В работе Экономические гармонии он пишет Природа, создающая все, даже самое великое, простейшими средствами, так устроила социальный порядок, что действия, в своей причине лишенные нравственного элемента, т.е. исходящие из собственного интереса, тем не менее, ведут к тем же результатам, каких ожидают моралисты от добродетели, самообладания и человеколюбия, т.е. к всеобщему благополучию . Другими словами, состояния общего блага можно, достичь, не опираясь на нравственные чувства и человеколюбивое настроение. Данное убеждение сыграло большую роль в процессе высвобождения экономических отношений из социальных и культурных норм в пользу большего подчинения экономики собственным законам, большего воздействия экономических закономерностей на распределение благ и социальную структуру общества. [c.26]
