Из теоретических законов для описания статистических распределений межпоездных интервалов наибольшее применение находит распределение Эрланга. Установлено, что для предприятий с внешним прибытием до 10 млн т в год распределение межпоездных интервалов удовлетворительно описывается законом Эрланга первого порядка или показательным законом, для предприятий с внешним прибытием 10 млн. т в год и более — по закону Эрланга второго порядка. [c.56]
F (/,.)= -< -", а функции распределения Эрланга второго порядка [c.56]
Обобщенное распределение Эрланга. Обычно распределение Эрланга используется в случаях, когда длительность какого-либо процесса можно представить как сумму k элементарных последовательных составляющих, распределенных по экспоненциальному закону. Если обозначить математическое ожидание длительности всего процесса как Щ = 1К, среднюю длительность элементарной составляющей как 1/Я., то плотность вероятностей распределения Эрланга представляется следующей формулой [c.33]
Предположим, что в распределении Эрланга имеется не строго фиксированное число экспоненциально распределенных отрезков k, а переменное, с вероятными изменениями в пределах одного интервала. Тогда можно говорить лишь о средней величине s таких отрезков, где s - число с плавающей точкой. После такого перехода от дискретных к непрерывным величинам появляется возможность работы и со значениями в пределах 0 < s < 1. [c.33]
| Рис. 1.5. Вид распределения Эрланга при различных значениях k 1 - экспоненциальное 2, 3 - распределения второго и третьего порядков | 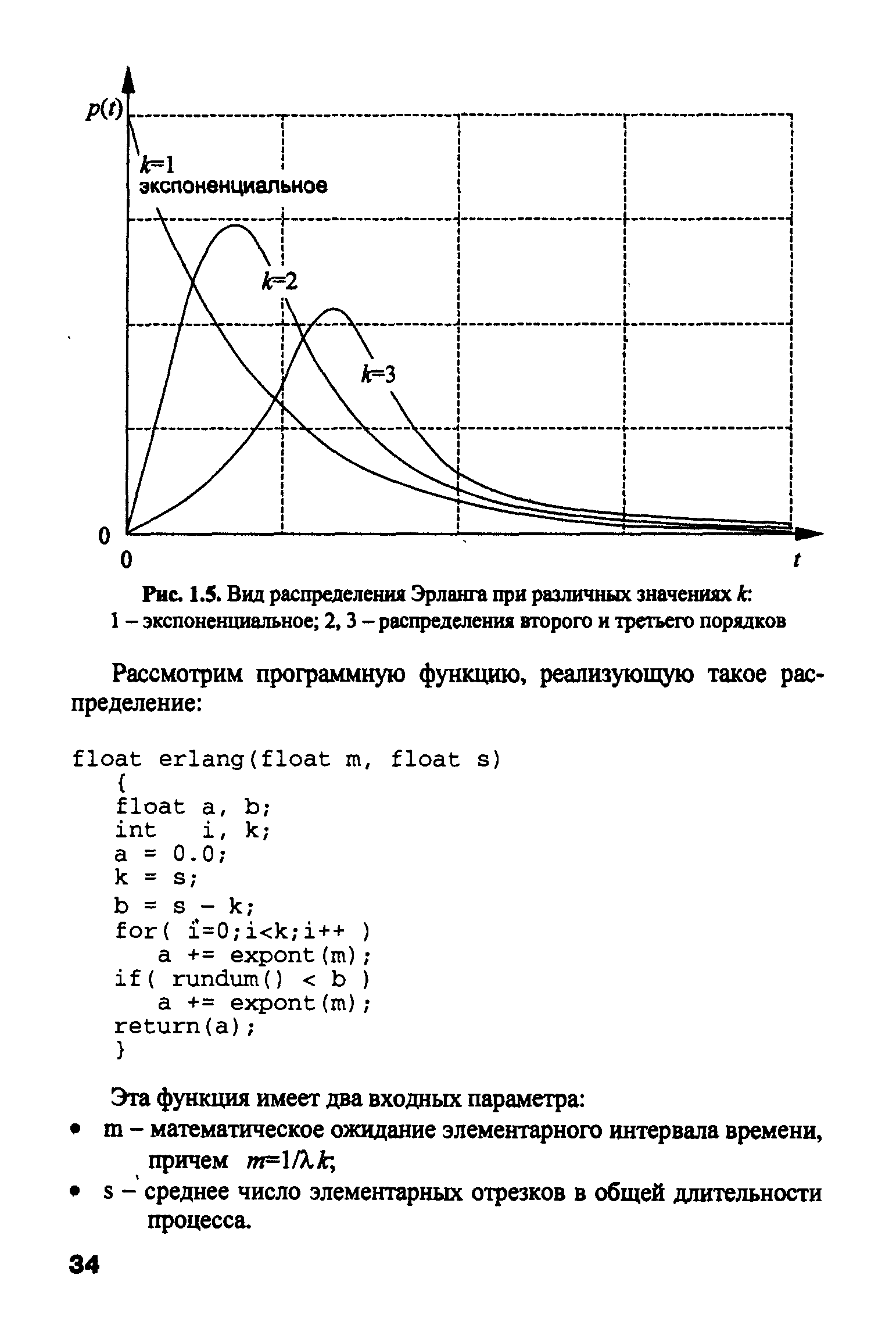 |
Обобщенное распределение Эрланга применяется при создании как чисто математических, так и имитационных моделей в двух случаях. [c.35]
Во-вторых, в реальной жизни существует объективная вероятность возникновения групп заявок в качестве реакции на какие-то действия, поэтому возникают групповые потоки. Применение чисто математических методов для исследования в моделях эффектов от таких групповых потоков либо невозможно из-за отсутствия способа получения аналитического выражения, либо затруднено, так как аналитические выражения содержат большую систематическую погрешность из-за многочисленных допущений, благодаря которым исследователь смог получить эти выражения. Для описания одной из разновидностей группового потока можно применить обобщенное распределение Эрланга, которое рассмотрим ниже. Внешне похожее на гамма-распределение, оно имеет свои математические особенности. [c.36]
Одно из свойств групповых потоков заключается в том, что а превосходит математическое ожидание интервала между заявками, поэтому коэффициент вариации с>. Формула для оценки среднего размера группы заявок при обобщенном распределении Эрланга имеет вид [c.50]
Это соотношение позволяет отслеживать появление групповых потоков в реальных системах или в их имитационных моделях. Особенность обобщенного распределения Эрланга заключается в том, что его применение позволяет выполнить расчет на худший случай (при перегрузках). [c.50]
Для чего используется обобщенное распределение Эрланга [c.57]
Г. Гамма-распределение и распределение Эрланга. Неотрицательная случайная величина X имеет гамма-распределение, если ее плотность распределения вычисляется по формуле [c.31]
При целом k > 1 гамма-распределение превращается в распределение Эрланга k-то порядка, т. е. [c.31]
Опишем процесс преобразования предприятий в акционерные общества и предприятия частной формы собственности при помощи законов распределения Эрланга (4.5). [c.168]
Распределение Эрланга и экспоненциальное распределение — это специальные случаи гамма-распределения. Гамма-распределение имеет функцию плотности [c.273]
Какой формулой выражается закон распределения Эрланга k-то порядка [c.121]
Распределение Эрланга г-го порядка имеет плотность [c.69]
Оно является обобщением распределения Эрланга на случай нецелых а > 0. Поэтому его нельзя считать фазовым. На рис. 3.3 показано несколько типичных графиков гамма-плотности с одинаковым средним a/fj, — 1 и различными a. Случай а — 1 соответствует показательному закону. [c.72]
Для подсчета распределения числа требований простейшего потока за время t выполним свертку показательных распределений. Их свертка А--го порядка есть распределение Эрланга того же порядка (см. разд. 3.3.1). Вероятность появления на интервале длины / ровно А заявок равна Fb+i(t) — Fj.(/). Подставляя в это выражение формулу (3.3.2), убеждаемся, что вероятность прихода за [0,/) ровно А требований [c.80]
Наиболее сложен для расчета вариант, когда Ar < s, a j > s — k. В этом случае новый индекс k + j > s и первые m — s — k заявок при постоянной интенсивности потока XR прибывают за время, подчиненное распределению Эрланга порядка m. После этого происходит выборка n = AT + j — s элементов из R оставшихся. Для упрощения обозначений введем вспомогательные коэффициенты [c.292]
При большом J и однородных базах с AJ — в получим АО = J B Времена между заказами для этой объединенной базы имеют распределения Эрланга порядка QB со средним [c.328]
Сам вид функции // (иг), характеризующий одно и то же понятие, процесс или объект разные специалисты могут формировать по-разному. Один считает, что для данного объекта она симметрична и имеет вид равнобедренного треугольника, другой - что это трапеция, а третий - что она имеет вид фигуры неправильной формы. В этом принципиальное отличие функции А(и от функции распределения в теории вероятностей. Сотнями экспериментов установлено, что рассеивание снарядов артиллерийских орудий подчиняется закону рассеивания Гаусса. И ни один специалист не имеет права считать, что оно подчиняется какому-нибудь другому закону распределения, например Эрланга. Если он так считает, он должен это доказать. Таким образом, функция JUA(UJ) - это функция, определяющая субъективное [c.287]
По специальной таблице, приводимой в курсах по теории вероятностей для X и г, определяем вероятность приближений опытной кривой к теоретическому распределению. Эта вероятность равна Р=0,19. Следовательно, гипотезу о распределении интервалов прибытия поездов на станцию по закону Эрланга можно считать правдоподобной. [c.55]
Если задача позволяет использовать теоретическое распределение, то данный блок может работать как преобразователь С, где, например, случайный поток с равномерным распределением преобразуется в поток Эрланга или другой тип распределения. [c.291]
Обобщенный закон Эрланга - закон распределения случайных величин, имеющий несимметричный вид. Занимает промежуточное положение между экспоненциальным и нормальным. В имитационных моделях экономических процессов используется для моделирования сложных групповых потоков заявок (требований, заказов). [c.353]
При имитационном моделировании поток событий чаще всего воспроизводится через интервалы времени между соседними событиями. Если время между соседними событиями случайно, то в зависимости от вида распределения воспроизведение его в ЭВМ происходит в соответствии с теми способами, которые были рассмотрены при имитации непрерывных случайных величин, причем случайной величиной является длительность интервала между соседними событиями. Например, для простейшего потока событий время между событиями подчинено показательному закону следовательно, имитация данного потока должна происходить в соответствии с выражением (9.4). Модификация простейшего потока — поток Эрланга — получается в результате имитации простейшего потока и последующего просеивания его событий в соответствии с порядком этого потока. Регулярный поток в системе легко имитируется, так как он задается постоянным временем интервала между событиями. Аналогичным образом могут быть смоделированы и потоки более общего вида через задание соответствующего распределения интервалов между соседними событиями в потоке. [c.208]
Равномерное распределение 33 Распределение Пуассона 26 - Эрланга 31 Регрессия 139 Регрессионный анализ 141 Риск 309 [c.426]
Потоком Эрланга k-ro порядка называется поток событий, получающийся прореживанием простейшего потока, когда сохраняется каждая k+1-я точка в потоке, а все промежуточные выбрасываются. Например, если в простейшем потоке сохраняется каждая вторая точка, то образуется поток Эрланга первого порядка. Поток Эрланга второго порядка получится, если сохранить в простейшем потоке каждую третью точку, а две промежуточные выбросить. Интервал времени между двумя соседними событиями в потоке Эрланга k-ro порядка представляет сумму k независимых случайных величин Ti,T2,...,Tk, имеющих показательное распределение с параметром /I, т.е. [c.156]
Закон распределения случайной величины Т называется законом Эрланга А -го порядка и имеет плотность [4.1] [c.156]
Законы распределения (4.5) были впервые получены выдающимся датским ученым А.Эрлангом, одним из первых исследователей и создателей теории массового обслуживания (ТМО). А.Эрланг пришел к этим законам, исследуя практические задачи ТМО (в 1909-1922 гг.), возникшие в начале XX века в связи с проблемами организации телефонных сетей. [c.157]
Марковские процессы могут быть не только с дискретным числом состояний, но и непрерывными. Простейший поток событий является частным случаем марковского случайного процесса с дискретными состояниями. Поскольку мы имеем дело с процессами рождения, выживания и развития новых экономических субъектов — индивидуальных предпринимателей, фермерских и крестьянских хозяйств, малых и средних предприятий, которые являются простейшими потоками событий, нам достаточно ограничиться законами распределения описывающими простейшие потоки. Этими законами являются законы Эрланга, приведенные выше (4.5). [c.158]
В нашем исследовании, мы имеем дело с л-ым предпринимателем, который выжил в условиях жесткой конкуренции и нашел свою нишу на рынке, или m-ым фермерским хозяйством, которое сумело наладить прибыльное сельскохозяйственное производство, или А -ым малым предприятием, сумевшим организовать рентабельное производство товаров, пользующихся спросом на рынке. Ясно, что распределение подобных субъектов описывается законом Эрланга соответствующего порядка. Поэтому законы Эрланга можно назвать законами выживания новых экономических субъектов. Как мы увидим в последующих параграфах процессы выживания и развития [c.158]
Поскольку каждое второе предприятие преобразуется в акционерное общество (АО), распределение АО по годам описывается законом Эрланга ого порядка [c.169]
Итак, в реальном случае, когда состоялось каждое второе ФКХ, распределение ФКХ может быть представлено законом Эрланга первого порядка [c.179]
Необходимо также рассмотреть идеальный случай, когда каждое зарегистрированное ФКХ состоялось. В этом случае распределение ФКХ опишется законом Эрланга первого порядка. Поэтому имеем [c.180]
Статистика показывает, что в Кыргызстане каждый второй из официально зарегистрированных индивидуальных частных предпринимателей выжил и более или менее успешно работает на рынке, получая прибыль. Следовательно, распределение индивидуальных частных предпринимателей (в дальнейшем, сокращенно - ИЧП) по числу выживаемости можно записать законом Эрланга первого порядка [c.185]
В данном примере мы рассмотрели самый простой случай пуассоновский входной поток, экспоненциальное время обслуживания, одна обслуживающая установка. На самом деле, в реальности, и распределения бывают значительно сложнее, и АЗС включают в себя большее число бензоколонок. Для того чтобы упорядочить классификацию систем массового обслуживания, американский математик Д. Кен-далл предложил удобную систему обозначений, широко распространившуюся к настоящему времени. Тип системы массового обслуживания Кендалл обозначил с помощью трех символов, первый из которых описывает тип входного потока, второй — тип вероятностного описания системы обслуживания, а третий — количество обслуживающих приборов. Символом М он обозначал пуассоновское распределение входного потока (с экспоненциальным распределением интервалов между заявками), этот же символ применялся и для экспоненциального распределения продолжительности обслуживания. Таким образом, описанная и изученная в этом параграфе система массового обслуживания имеет обозначение М/М/1. Система M/G/3, например, расшифровывается как система с пуассоновским входным потоком, общей (по-английски — general) функцией распределения времени обслуживания и тремя обслуживающими устройствами. Встречаются и другие обозначения D —детерминированное распределение интервалов между поступлением заявок или длительностей обслуживания, Е — распределение Эрланга порядка п и т. д. [c.211]
Распределение Эрланга дает меньшую неравномерность интервалов, чем экспоненциальное, что характерно для более интенсивного поездопотока. [c.56]
Сеть процессов, образующих учебный план, - довольно сложная, полнодоступная. Поэтому в практических расчетах будем считать, что поток групп - пуассоновский, а размер группы распределен по закону обобщенного распределения Эрланга. [c.50]
Поток с ограниченным последействием поток Пальма поток Эрланга k-то порядка закон распределения Эрланга k-то порядка с параметром Я нормированный поток Эрланга k-то порядка центральная предельная теорема для одинаково распределенных слагаемых случайных величин сходимость по вероятности мера последействия нормальное распределение нормальная кривая кривая Гаусса Гаусс К.Ф. Чебышёв П.Л. [c.121]
Распределение Эрланга — двухпараметрическое, причем г должно быть целым. Это обстоятельство определяет следующую схему подбора параметров распределения Эрланга [c.70]
Численные эксперименты показали, что особыми случаями для Нп -аппроксимации являются любые распределения Эрланга порядка k < п. Это вполне естественно, поскольку последние предполагают последовательную систему фаз, тогда как гиперэкспонента — параллельную. [c.71]
