Марковских процессов 187 Модель [c.883]
Рассматривается однородный марковский процесс принятия решений [c.53]
Среди важнейших классов задач И.о. можно назвать задачи управления запасами, распределения ресурсов и задачи назначения (распределительные задачи), задачи массового обслуживания, задачи замены оборудования, упорядочения и согласования (в том числе теории расписаний), состязательные (напр., игры), задачи поиска и др. Среди применяемых методов —математическое программирование (линейное, нелинейное и т.п.), дифференциальные и разностные уравнения, методы теории графов, марковские процессы, теория игр, теория (статистических) решений, теория распознавания образов и ряд других. [c.136]
Для экономических исследований большое значение имеет также анализ стохастических процессов, в т.ч. "марковских процессов". [c.184]
Основу этих методов составляют теория вероятностей, теория марковских процессов, теория массового обслуживания. [c.188]
Марковские процессы с непрерывным временем позволяют оперировать не только с вероятностями пребывания системы в своих состояниях, но и непосредственно с самими элементами (параметрами) системы. Для этого может быть использован метод динамики средних. [c.341]
Для решения задач такого рода используются различные математические методы — от аппарата теории функций комплексного переменного до стохастических уравнений и марковских процессов. До сих пор нет, однако, общего подхода, позволяющего рассматривать различные модели фильтрации и прогнозирования с единой точки зрения. Еще в большей мере отсутствие общей методологической основы сказывается на продвижении в теории пространственно-временного сглаживания и упреждения случайных полей, представляющей собой теоретическую базу обработки многопараметрической информации. Оценка и сравнение современных подходов к управлению в условиях неполной информации дает основание заключить, что наиболее естественной основой для си-38 [c.38]
Сигнал, спектральная плотность которого — дробно-рациональная функция частоты, можно представить как реакцию линейной системы на белый шум. Другими словами, такой сигнал может быть получен как решение линейного стохастического дифференциального уравнения, возмущаемого белым шумом. Случайный процесс — решение соответствующих стохастических дифференциальных уравнений — представляет собой марковский процесс или проекцию марковского процесса. Статистические характеристики марковских процессов — переходные вероятности — удовлетворяют известным дифференциальным уравнениям в частных производных А. Н. Колмогорова. Для вычисления условного математического ожидания М[т (0] гауссовского марковского процесса можно получить обыкновенное дифференциальное уравнение. Таким образом, выражение (4.8) для решения задачи (4.1) позволяет свести вычисление характеристик оптимальной в смысле задачи (4.1) фильтра- [c.315]
При имитационном моделировании применяется много математических схем конечные и вероятностные автоматы, системы массового обслуживания (СМО), агрегативные системы, системы, описываемые дифференциальными уравнениями и марковскими процессами, методы общей теории систем, а также специально сконструированные эвристические подходы для конкретных типов объектов моделирования. Применительно к экономическим объектам и процессам наиболее часто используются, на наш взгляд, математические схемы СМО, агрегативные системы, а также эвристические подходы. Кроме этого, отдельные элементы метода статистических испытаний или метода Монте-Карло, которые лежат в основе имитационного моделирования, применяются достаточно часто при расчете различных параметров для других типов моделей — эконометрических, моделей кривых роста и т.п. В данной главе будут рассмотрены имитационные модели СМО и агрегативные имитационные модели. Естественно, приведенные ниже математические схемы ни в коей мере не исчерпывают их перечень. Кроме того, часто при имитационном моделировании применяется сочетание различных математических подходов, поэтому дать весь перечень применяемых математических схем затруднительно, да и вряд ли целесообразно. Главное — наличие имитационного мышления при выборе тех или иных математических подходов. [c.229]
Существует целое семейство марковских процессов некоторые, такие, как биномиальные и триномиальные модели, мы уже встречали. В этой главе мы рассмотрим три процесса непрерывного времени/непрерывной переменной основной процесс Винера, обобщенный процесс Винера и процесс Ито. [c.463]
Объясните, как вы понимаете термин "марковский процесс". [c.481]
Предположим, что состояния образуют марковский процесс первого порядка. Если в момент t рынок находился в состоянии s(, тогда в момент / + 1 он будет находиться в состоянии s,+1 с заданной вероятностью. Существуют три типа платежей по ценной бумаге х [c.201]
Б а р у ч а-Р и д А. Т. Элементы теории марковских процессов и их приложения. Пер. с англ. —М. Наука, 1969. — 511 с. [c.460]
X о в а р д Р. А., Динамическое программирование и марковские процессы, изд-во Сов. радио , 1964. [c.299]
| Рис. 2.3. Диаграмма переходов марковского процесса, моделирующего функционирование элемента с частичными отказами | 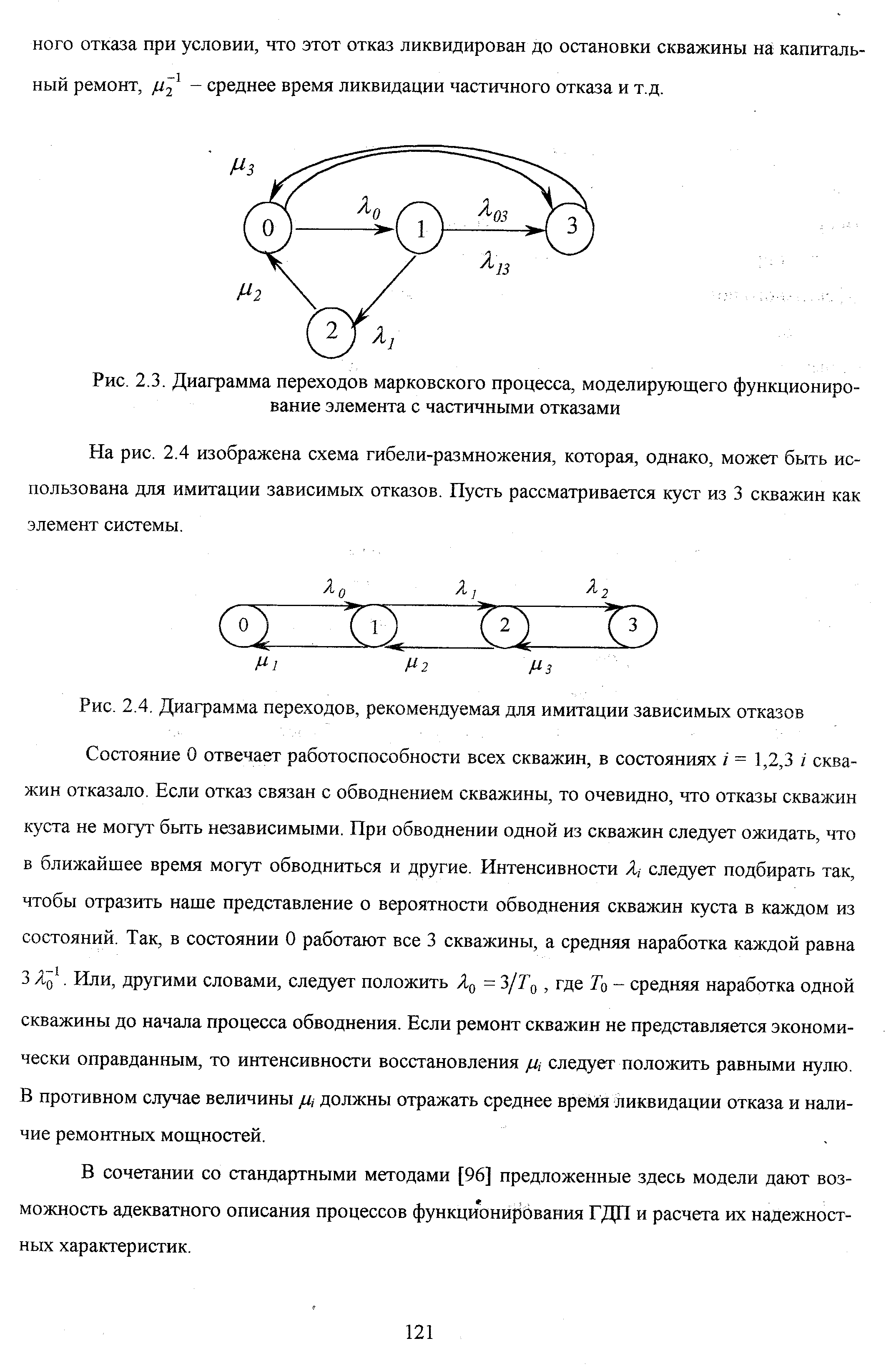 |
Выражение под знаком суммы в (4.1.2) совпадает с понятием доход для управляемого марковского процесса [152] при переходе из состояния %(т) в состояние (г+7). Когда множества 3(/) состояний среды заданы и для каждого управления u(t) eU(f) определены переходные вероятности P(f) = [р//(м(/) , i- j, /eE(/), /eS (/+/) и "доходы" (приросты дисконтированной стоимости при выборе управлений), формирование управляемого марковского процесса считается законченным и можно приступить к расчету оптимальной стратегии. [c.267]
МАРКОВСКИЙ ПРОЦЕСС [Markov pro ess] — дискретный или непрерывный случайный процесс X t), который можно полностью задать с помощью двух величин вероятности P(x,t) того, что случайная величина x t) в момент времени [c.182]
Трудности, связанные с неэргодичностью природных явлений (неоднородностью процессов во времени), можно преодолеть путем усреднения не по времени, а по реализациям, в качестве которых, например, могут быть взяты многолетние значения гидрометеовеличин, относящиеся к стандартным срокам наблюдений. Поскольку реализации принадлежат разным годам, то их с достаточным основанием можно считать статистически независимыми. Необходимо отметить, что наблюдения на гидрометеопостах представляют собой дискретное множество состояний природной системы. В каждый момент времени система находится в одном из них и с течением времени переходит из одного состояния в другое. Последовательность таких случайных состояний можно рассматривать как марковский процесс без последействия (цепь Маркова). [c.111]
Markov Pro ess (марковский процесс) Процесс, связывающий текущее значение переменной с ее предыдущими значениями и случайным остаточным членом. Простым примером является марковский процесс первого порядка, который имеет следующий вид [c.313]
Стратонович Р. Л. Условные марковские процессы и их применение к теории оптимального управления. Изд-во МГУ, 1966. [c.390]
Используя так называемый марковский процесс, который учитывает эволюцию каждого элемента системы, в [Л. 6] приводится формальный математический анализ функции готовности. Что касается настоящей работы, то качественное рассмотрение вопроса является достаточным. Вероятность возникновения аварийных режимов и влияние их на стоимость и Надежность электропередачи изучаются с целью оптимизации надежности и стоимости во многих странах, а также в шестом и седьмом комитетах СИГРЭ. Изменения в этой области можно проиллюстрировать, обращаясь опять к процессу проектирования воздушной линии передачи. [c.200]
Согласно части финансовой теории, известной как гипотеза эффективных рынков (effi ient market hypothesis, EMH), цены активов отображают всю историческую информацию, касающуюся этого актива, и немедленную реакцию на поступающую новую информацию по этому активу. Эта ответная реакция проявляется в виде изменения цены. Если действительно рынки немедленно реагируют на новую информацию и каждая часть новой информации независима от предыдущей, изменения в ценах активов будут следовать марковскому процессу. [c.463]
Марковские процессы характеризуются тем, что каждое последующее стояние зависит только от предыдущего, но не зависит от того, как оно. 1ло достигнуто. Большинство популяционныч процессов — марковские. 1 пример, численность населения в следующем году зависит только от чис-нности и уровня рождаемости в предыдущем. [c.633]
Автор считал, что поведение контролируемого параметра во времени описывается марковским процессом и исходя из этого указал способ определения числа корректировок процесса и числа дефектных единиц продукции, которые в среднем встречаются в заданном промежутке времени. Дальнейшее развитие применения марковских процессов для описания процесса разладки нашло отражение в работе Кнаппен-бергера и Грендейджа [128]. [c.131]
ТЕОРИЯ ВЕРОЯТНОСТЕЙ. математпч. наука, позволяющая по вероятностям одних случайных событий находить вероятности др. случайных событий, связанных к.-л. образом с первыми. Практически полезные результаты с помощью Т. в. могут быть получены, если исследователю удаётся описать (чаще — удовлетворительно аппроксимировать) изучаемый объект вероятностной математпч. моделью. Обычно в экономике прибегают к вероятностным математич. моделям при неполной или искажённой информации об изучаемом объекте, при изучении систем, состоящих пз большого количества элементов (когда детерминированные подходы исчерпывают себя), при изучении закономерностей, к-рые заведомо не являются детерминистическими. Примерами таких моделей могут служить модели теории спроса п потребительских предпочтений, вероятностные модификации классических моделей роста п равновесия, модели распределитель-ских отношений в обществе, модели демографич. процессов, опирающиеся на марковские процессы н т. д. В нек-рых из перечисленных ситуаций вероятностные модели не единственно пригодные. Т. в. является основой для таких разделов математики, используемых [c.108]
Число требований в СО, время ожидания. Пусть /( — число заявок в СО в момент t. Обозначим nj(t) = = P lt = j . Для простейшей системы Л/ /Л/ /1/ , случайный процесс является марковским процессом, а точнее процессом рождения и гибели, техника исследования к-рого хорошо разработана. В этом случае для Uj(t) можно составить систему дифференциальных уравнений Колмогорова и решить её в явном виде. Для более сложных систем найти nj(t) в явном виде, как правило, не удаётся. В Т. м. о. наибольшее внимание уделяется исследованию стационарного режима, к-рый описывает доведение системы при t— < > или поведение системы в конечные моменты времени, но при специальном выборе начального распределения величины /0 (если, конечно, такой режим существует). Для мн. СО условием существования стационарного режима является выполнение требования, чтобы коэффициент загрузки р (произведение среднего числа заявок, поступивших за единицу времени, на среднюю продолжительность обслуживания одной заявки в пересчёте на один канал) был меньше единицы. При р I число заявок в СО — <х> при t— oo. В этом случае система рассматривается в переходном режиме. Для системы Мь/Му./1/°о при р = Х/и, < 1 существуют jij = limitj (t) = pV(l — р), [c.118]
Смотреть страницы где упоминается термин Марковский процесс
: [c.882] [c.214] [c.53] [c.45] [c.202] [c.472] [c.735] [c.450] [c.124] [c.128] [c.128] [c.131] [c.239] [c.18] [c.316] [c.143] [c.463] [c.463] [c.133] [c.345] [c.110] [c.118]Экономико-математический словарь Изд.5 (2003) -- [ c.82 ]
Математические методы моделирования экономических систем Изд2 (2006) -- [ c.42 ]
