Основным признаком системы массового обслуживания является наличие некоторой системы (обслуживающей системы), которая предназначена для осуществления действий, совершаемых согласно требованиям (называемым заявками), которые поступают нерегулярным образом. Поскольку обслуживающая система обычно имеет ограниченную пропускную способность, а заявки поступают нерегулярно, время от времени создается очередь заявок в ожидании обслуживающего устройства иногда же оборудование простаивает в ожидании заявок. Наиболее часто предполагается, что известен вероятностный закон, управляющий поступлением заявок. Впервые такой подход был применен датским математиком А. К. Эрлангом в начале нашего века для анализа работы телефонной станции. С тех пор методы теории массового обслуживания распространились на широкий круг разнообразных проблем, включающий в себя столь разнородные задачи, как анализ очереди в магазине и исследование пропускной способности дорог, мостов и перекрестков, исследование эффективности работы большого морского порта и небольшой автозаправочной станции, анализ работы ремонтной бригады на предприятии и кассира в кинотеатре и т. д. Делаются попытки проанализировать с помощью методов теории массового обслуживания даже такие вопросы, как эффективность работы промышленного предприятия в целом. [c.200]
Питание микрофонов абонентских аппаратов осуществляется от комплектов реле соединительных линий районной АТС. Подстанция рассчитана на нагрузку 7,7 эрланг. [c.477]
Сам вид функции // (иг), характеризующий одно и то же понятие, процесс или объект разные специалисты могут формировать по-разному. Один считает, что для данного объекта она симметрична и имеет вид равнобедренного треугольника, другой - что это трапеция, а третий - что она имеет вид фигуры неправильной формы. В этом принципиальное отличие функции А(и от функции распределения в теории вероятностей. Сотнями экспериментов установлено, что рассеивание снарядов артиллерийских орудий подчиняется закону рассеивания Гаусса. И ни один специалист не имеет права считать, что оно подчиняется какому-нибудь другому закону распределения, например Эрланга. Если он так считает, он должен это доказать. Таким образом, функция JUA(UJ) - это функция, определяющая субъективное [c.287]
По полученным значениям M(t), D(t) и 8(t) определяют параметр Эрланга по входящему потоку /, среднечасовую интенсивность поступления поездов на промпредприятие К по формулам [c.54]
Далее определяется параметр Эрланга по входящему потоку и среднечасовой интенсивности прибытия поездов [c.55]
Для закона распределения Пуассона 5 = 2 для закона распределения Эрланга 5=3. В данном примере г=6 (9—3). [c.55]
По специальной таблице, приводимой в курсах по теории вероятностей для X и г, определяем вероятность приближений опытной кривой к теоретическому распределению. Эта вероятность равна Р=0,19. Следовательно, гипотезу о распределении интервалов прибытия поездов на станцию по закону Эрланга можно считать правдоподобной. [c.55]
Из теоретических законов для описания статистических распределений межпоездных интервалов наибольшее применение находит распределение Эрланга. Установлено, что для предприятий с внешним прибытием до 10 млн т в год распределение межпоездных интервалов удовлетворительно описывается законом Эрланга первого порядка или показательным законом, для предприятий с внешним прибытием 10 млн. т в год и более — по закону Эрланга второго порядка. [c.56]
F (/,.)= -< -", а функции распределения Эрланга второго порядка [c.56]
По формуле Эрланга рассчитывают вероятности одновременной занятости I рабочих из общего числа п (без старшего оператора) [c.206]
Часто используется также ординарный стационарный поток с отсутствием последействия, который называется потоком Эрланга. Потоком Эрланга порядка т называют поток, для которого [c.234]
Потоки событий различного вида могут разрежаться и объединяться [37]. К сожалению, эти термины могут применяться только к потокам определенного вида. Так, например, если интервалы в потоке Эрланга п -го порядка уменьшить в (п + 1) раз, то интенсивность полученного потока станет равной интенсивности исходного пуассоновского потока, и с ростом п такой поток становится сколь угодно близким к регулярному с той же интенсивностью. Такие нормированные потоки Эрланга дают различные типы потоков с последействием, начиная от потоков без последействия ( п = 1) и кончая регулярными (п = °°). [c.234]
Как будет показано ниже, используя потоки Эрланга и Пуассона, можно рассчитать аналитически установившиеся значения различных параметров СМО. Однако применение этих потоков в практике имитационного моделирования в чистом виде, без специальной корректировки, учитывающей изменения типа потока, его интенсивности и т.п. крайне ограничено. [c.235]
Если задача позволяет использовать теоретическое распределение, то данный блок может работать как преобразователь С, где, например, случайный поток с равномерным распределением преобразуется в поток Эрланга или другой тип распределения. [c.291]
Обобщенное распределение Эрланга. Обычно распределение Эрланга используется в случаях, когда длительность какого-либо процесса можно представить как сумму k элементарных последовательных составляющих, распределенных по экспоненциальному закону. Если обозначить математическое ожидание длительности всего процесса как Щ = 1К, среднюю длительность элементарной составляющей как 1/Я., то плотность вероятностей распределения Эрланга представляется следующей формулой [c.33]
Предположим, что в распределении Эрланга имеется не строго фиксированное число экспоненциально распределенных отрезков k, а переменное, с вероятными изменениями в пределах одного интервала. Тогда можно говорить лишь о средней величине s таких отрезков, где s - число с плавающей точкой. После такого перехода от дискретных к непрерывным величинам появляется возможность работы и со значениями в пределах 0 < s < 1. [c.33]
| Рис. 1.5. Вид распределения Эрланга при различных значениях k 1 - экспоненциальное 2, 3 - распределения второго и третьего порядков | 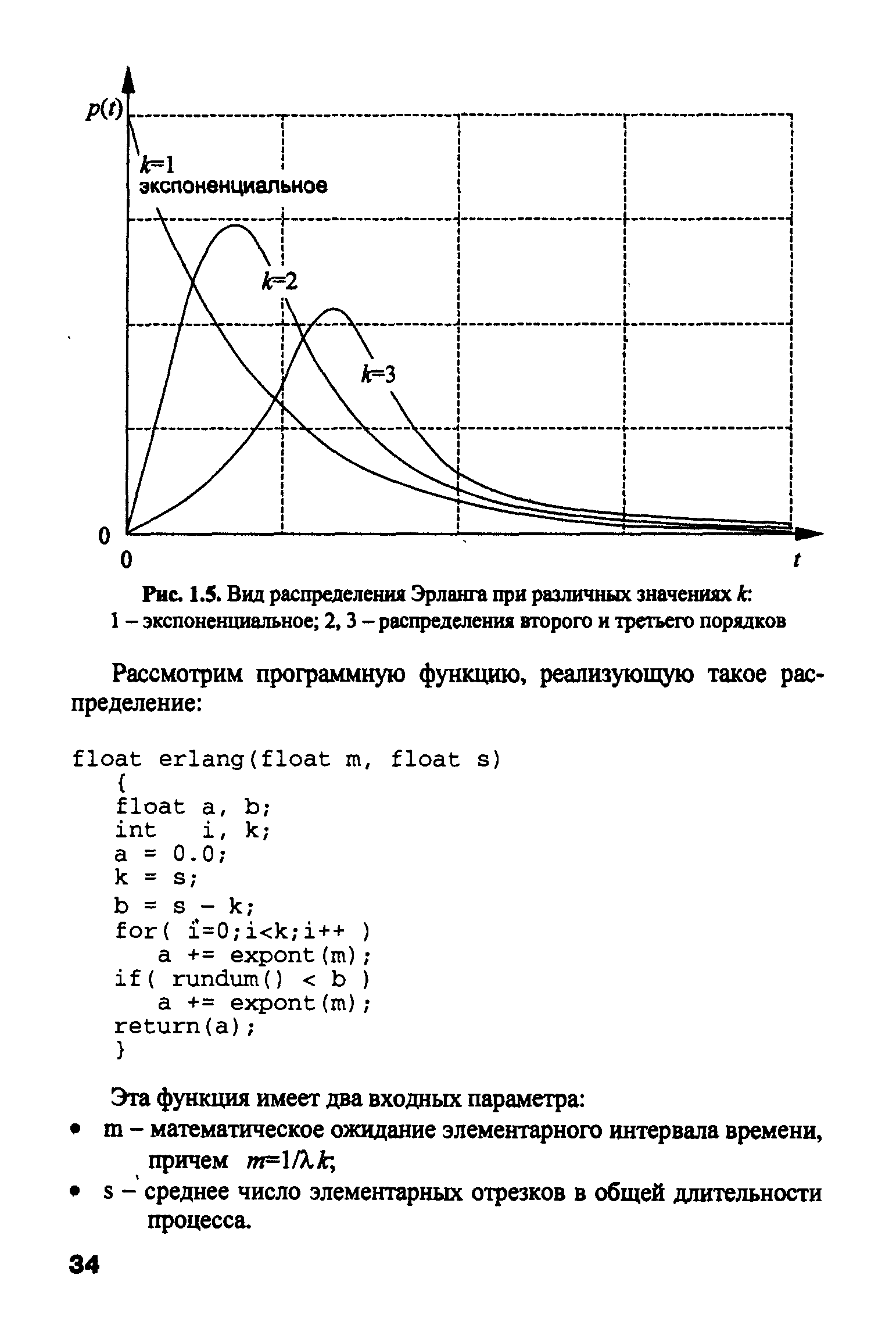 |
Обобщенное распределение Эрланга применяется при создании как чисто математических, так и имитационных моделей в двух случаях. [c.35]
Во-вторых, в реальной жизни существует объективная вероятность возникновения групп заявок в качестве реакции на какие-то действия, поэтому возникают групповые потоки. Применение чисто математических методов для исследования в моделях эффектов от таких групповых потоков либо невозможно из-за отсутствия способа получения аналитического выражения, либо затруднено, так как аналитические выражения содержат большую систематическую погрешность из-за многочисленных допущений, благодаря которым исследователь смог получить эти выражения. Для описания одной из разновидностей группового потока можно применить обобщенное распределение Эрланга, которое рассмотрим ниже. Внешне похожее на гамма-распределение, оно имеет свои математические особенности. [c.36]
Одно из свойств групповых потоков заключается в том, что а превосходит математическое ожидание интервала между заявками, поэтому коэффициент вариации с>. Формула для оценки среднего размера группы заявок при обобщенном распределении Эрланга имеет вид [c.50]
Это соотношение позволяет отслеживать появление групповых потоков в реальных системах или в их имитационных моделях. Особенность обобщенного распределения Эрланга заключается в том, что его применение позволяет выполнить расчет на худший случай (при перегрузках). [c.50]
Для чего используется обобщенное распределение Эрланга [c.57]
Обобщенный закон Эрланга - закон распределения случайных величин, имеющий несимметричный вид. Занимает промежуточное положение между экспоненциальным и нормальным. В имитационных моделях экономических процессов используется для моделирования сложных групповых потоков заявок (требований, заказов). [c.353]
По мере роста многообразия форм производственных связей, усложнения технологических процессов, развития технических средств для процесса управления меняется отношение к формализованным оценкам и методам, являющимся, в определенном смысле, материальной основой принятия управленческих решений. В частности, в 1915 г. Ф.Харрисом была предложена идея оптимальной партии заказа для управления запасами, в 1917 г. А.Эрлангом разработана теория очередей для прогнозирования времени ожидания при использовании автоматических телефонных станций и др. [c.7]
ЭРЛАНГ - международная единица загрузки транспортного средства товарами. [c.873]
ЭРЛАНГ — международная единица загрузки товарами транспортного средства. [c.469]
При имитационном моделировании поток событий чаще всего воспроизводится через интервалы времени между соседними событиями. Если время между соседними событиями случайно, то в зависимости от вида распределения воспроизведение его в ЭВМ происходит в соответствии с теми способами, которые были рассмотрены при имитации непрерывных случайных величин, причем случайной величиной является длительность интервала между соседними событиями. Например, для простейшего потока событий время между событиями подчинено показательному закону следовательно, имитация данного потока должна происходить в соответствии с выражением (9.4). Модификация простейшего потока — поток Эрланга — получается в результате имитации простейшего потока и последующего просеивания его событий в соответствии с порядком этого потока. Регулярный поток в системе легко имитируется, так как он задается постоянным временем интервала между событиями. Аналогичным образом могут быть смоделированы и потоки более общего вида через задание соответствующего распределения интервалов между соседними событиями в потоке. [c.208]
Г. Гамма-распределение и распределение Эрланга. Неотрицательная случайная величина X имеет гамма-распределение, если ее плотность распределения вычисляется по формуле [c.31]
При целом k > 1 гамма-распределение превращается в распределение Эрланга k-то порядка, т. е. [c.31]
Закону Эрланга k-то порядка подчинена сумма независимых случайных величин Xj + х2 +. .. + xk, каждая из которых распределена по показательному закону с параметром Я. [c.31]
Формулы для вычисления вероятностей Pk называются формулами Эрланга. [c.98]
Равномерное распределение 33 Распределение Пуассона 26 - Эрланга 31 Регрессия 139 Регрессионный анализ 141 Риск 309 [c.426]
Классическая задача теории массового обслуживания, решение которой дал К.Эрланг, состоит в оценке вероятностей попадения в то или иное состояние, если требования, застающие все приборы системы занятыми обслуживанием ранее появившихся требований, теряются безвозвратно. Это пример так называемых систем "без очередей", к которым и относится система обслуживания технологических установок ШЗ. В системах данного класса любое действие по обслуживанию оборудования должно быть выполнено немедленно по возникновении необходимости в нем. В противном случае требование на обслуживание будет потеряно безвозвратно, что в применении к обслуживанию технологической установки означает невыполнение какого-либо действия по регулированию процесса и может вызвать аварию. Следовательно, в Данном конкретном случае решение задачи состоит в отыскании такого минимального числа обслуживающих устройств (рабочих), при котором ни одно требование [c.44]
Сам К.Эрланг изучал эту задачу в следующих предположениях поток требований - пуассоновский с интенсивностью J длительность обслуживания распределена по показательному закону, причем средняя продолжительность обслуживания . При названных предположениях К.Эрланг показал, что если число обслуживающих устройств равно /7 , то при стационарном пуас-соновском потоке требовании вероятности / ( t, ) (вероятность того, что в момент Г обслуживанием заняты приборов) близки к их предельным значениям 1 [c.45]
В данном примере мы рассмотрели самый простой случай пуассоновский входной поток, экспоненциальное время обслуживания, одна обслуживающая установка. На самом деле, в реальности, и распределения бывают значительно сложнее, и АЗС включают в себя большее число бензоколонок. Для того чтобы упорядочить классификацию систем массового обслуживания, американский математик Д. Кен-далл предложил удобную систему обозначений, широко распространившуюся к настоящему времени. Тип системы массового обслуживания Кендалл обозначил с помощью трех символов, первый из которых описывает тип входного потока, второй — тип вероятностного описания системы обслуживания, а третий — количество обслуживающих приборов. Символом М он обозначал пуассоновское распределение входного потока (с экспоненциальным распределением интервалов между заявками), этот же символ применялся и для экспоненциального распределения продолжительности обслуживания. Таким образом, описанная и изученная в этом параграфе система массового обслуживания имеет обозначение М/М/1. Система M/G/3, например, расшифровывается как система с пуассоновским входным потоком, общей (по-английски — general) функцией распределения времени обслуживания и тремя обслуживающими устройствами. Встречаются и другие обозначения D —детерминированное распределение интервалов между поступлением заявок или длительностей обслуживания, Е — распределение Эрланга порядка п и т. д. [c.211]
ЭРЛАНГА ФОРМУЛЫ [A.Erlang s formulae] в теории массового обслуживания — формулы, выражающие вероятность отказа для систем обслуживания с потерями (см. Система массового обслуживания). Формулы были выведены шведским инженером А. Эрлангом в 20-е гг. XX в. при решении задач, связанных с проектированием телефонных линий, для определения их оптимальной загрузки. [c.427]
Эйдельман М.Р. 193,406 Энгель Э. 272, 339, 380, 381, 399, 427, 454 Энгельс Ф. 272, 322 Эрланг А. 427 Эрроу К. 186, 203, 219, 313, 356, 396, 427, [c.457]
Распределение Эрланга дает меньшую неравномерность интервалов, чем экспоненциальное, что характерно для более интенсивного поездопотока. [c.56]
Сеть процессов, образующих учебный план, - довольно сложная, полнодоступная. Поэтому в практических расчетах будем считать, что поток групп - пуассоновский, а размер группы распределен по закону обобщенного распределения Эрланга. [c.50]
Начало Т, м. о. было положено датским ученым А. К. Эрлангом в начале 20 в. применительно к задачам, возникавшим при проектировании телефонных станций. Задачами многостаночного обслуживания занимался шведский ученый К. Пальм. Огромный вклад в Т. м. о. представляют работы сов. математиков А.Н.Колмогорова и А. Я. Хинчина. Над развитием Т. М. о. и расширением круга ее практич. применений работают многие ученые как в СССР, так и за рубежом. Лит. X и нч и н А. Я., Работы по математической теории массового обслуживания, М., 1963 Розенберг В. Я., Прохоров А. И., Что такое теория массового обслуживания, М., 1962 Вентцель Е. С., Теория вероятностей, М., 1962, гл. 19. Я. П. Герчук. [c.156]
