Рассмотрим алгоритм расчета факторов этим способом в моделях мультипликативно-аддитивного вида. Для примера возьмем факторную модель прибыли от реализации продукции [c.58]
Модель мультипликативная — жестко детерминированная факторная модель, в которую факторы входят в виде произведения. [c.535]
Влияние использования материальных ресурсов на величину материальных затрат оценивается с использованием двух-факторных моделей мультипликативная модель изучает влияние материалоемкости по прямым затратам и коэффициента соотношения общих и прямых затрат аддитивная модель — влияние материалоемкости отдельных видов материальных ресурсов на совокупный показатель материалоемкости. [c.242]
Аддитивная модель. Мультипликативная модель. Автокорреляция. Лаг. [c.23]
| Рис. 25. Математические модели мультипликативной (а) и аддитивной (б) температурной поправки в примере 21 | 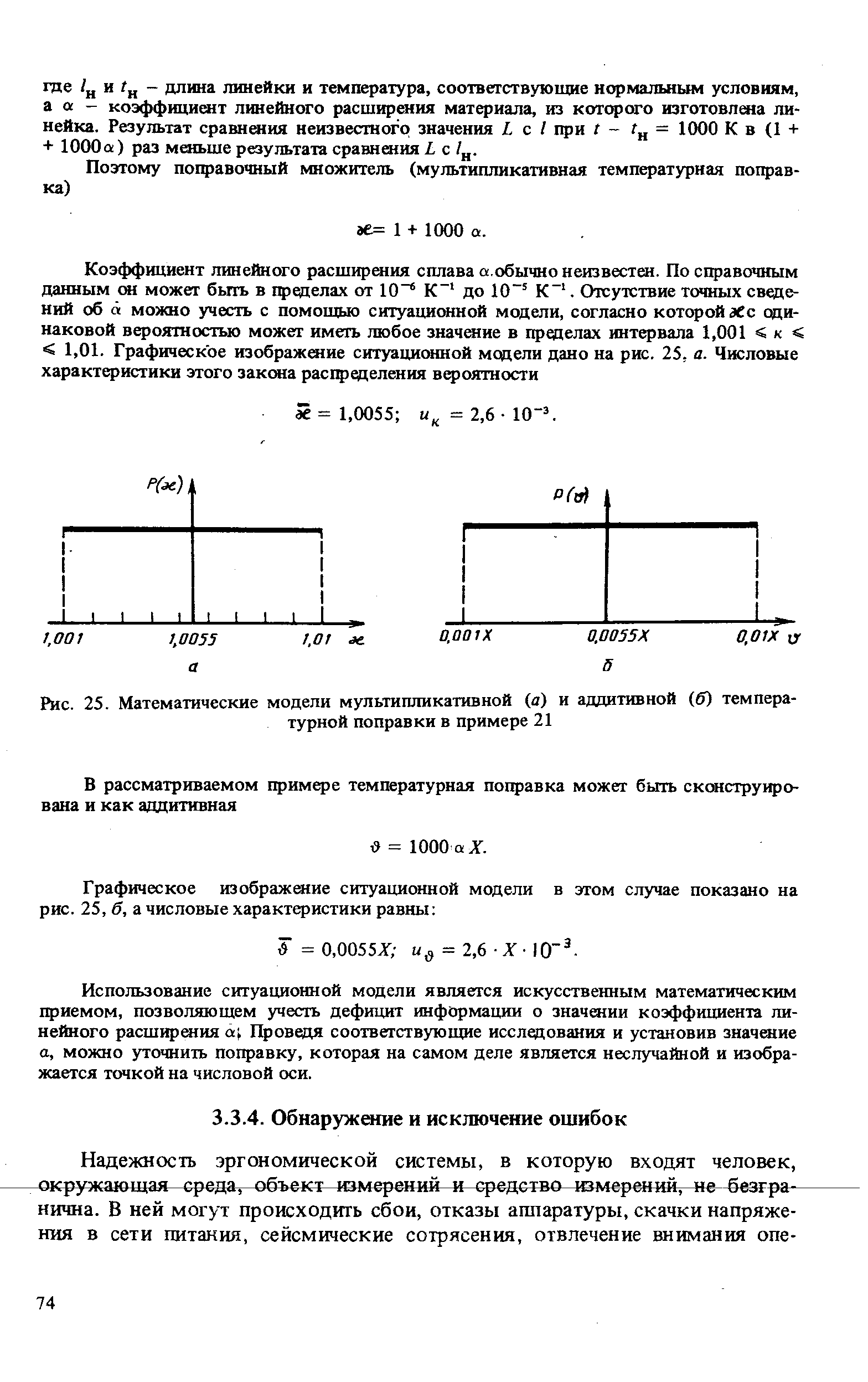 |
Строго говоря, все сезонные модели мультипликативны и имеют лишь один линейный элемент (роп), он и будет аддитивным. [c.28]
В данном случае для преобразования исходной факторной модели, построенной на математических зависимостях, использованы способы удлинения и расширения. В результате получилась более содержательная модель мультипликативно-аддитивно-кратного вида, которая имеет большую познавательную ценность, поскольку учитывает причинно-следственные связи между показателями. Данная модель позволяет исследовать, как влияют на доходность капитала объем продаж, отпускные цены, себестоимость реализованной продукции, внереализационные финансовые результаты, а также скорость обращения капитала. [c.96]
Итак, мы рассмотрели четыре способа выявления сезонной компоненты аддитивную модель, мультипликативную модель, метод экспоненциального сглаживания с тремя параметрами, гармонический анализ Фурье (рис. П-7). В нашем примере оказалось, что наименьшую ошибку дает мультипликативная модель, т. е. применение индексов сезонности. [c.439]
Поскольку модель мультипликативная, то применимы следующие способы ее обработки. [c.37]
Методика построения мультипликативных моделей эффективности производства. [c.106]
Вычислительная схема реализации расчетов по модели (2)— (9) на основе мультипликативного алгоритма симплекс. — метода показана на рисунке. [c.100]
Эти модели отражают процесс детализации исходной факторной системы мультипликативного вида и расширения ее за счет расчленения на сомножители комплексных факторов. Степень детализации и расширения модели зависит от цели исследования, атакже от возможностей детализации и формализации показателей в пределах установленных правил. [c.34]
В результате получается конечная мультипликативная модель в виде произведения нового набора факторов. [c.35]
Наиболее универсальным из них является способ цепной подстановки. Он используется для расчета влияния факторов во всех типах детерминированных факторных моделей аддитивных, мультипликативных, кратных и смешанных (комбинированных). Этот способ позволяет определить влияние отдельных факторов на изменение величины результативного показателя путем постепенной замены базисной величины каждого факторного показателя в объеме результативного показателя на фактическую в отчетном периоде. С этой целью определяют ряд условных величин результативного показателя, которые учитывают изменение одного, затем двух, трех и последующих факторов, допуская, что остальные не меняются. Сравнение величины результативного показателя до и после изменения уровня того или другого фактора позволяет элиминировать влияние всех факторов, кроме одного, и определить воздействие последнего на прирост результативного показателя. Порядок применения этого способа рассмотрим на примере, приведенном в табл. 4.1. [c.55]
Как нам уже известно, объем валовой продукции (ВП) зависит от двух основных факторов первого порядка численности рабочих (ЧР) и среднегодовой выработки (ГВ). Имеем двухфакторную мультипликативную модель [c.55]
Способ относительных разниц применяется для измерения влияния факторов на прирост результативного показателя только в мультипликативных моделях. Здесь используются относительные приросты факторных показателей, выраженные в виде коэффициентов или процентов. Рассмотрим методику расчета влияния факторов этим способом для мультипликативных моделей типа Y ab . [c.59]
Мультипликативные модели — модели умножения. Например, объем продукции может быть определен по выражению [c.85]
Для кратной формы связи, при тех же предположениях, что и для мультипликативной модели [c.273]
Корреляционная модель себестоимости добычи нефти и попутного газа по указанным факторам была рассчитана по мультипликативной функции Кобба — Дугласа (41). В результате решения этой модели было составлено сводное уравнение по нефтедобывающей промышленности Украинской ССР [c.90]
Основным недостатком логарифмического метода анализа является то, что он не может быть универсальным , его нельзя применять при анализе любого вида моделей факторных систем. Если при анализе мультипликативных моделей факторных систем при использовании логарифмического метода достигается получение точных величин влияния факторов (в. случае, когда Az = 0), то при таком же анализе кратных моделей факторных систем получение точных величин влияния факторов не удается. [c.126]
Формирование рабочих формул интегрального метода для мультипликативных моделей. Применение интегрального метода факторного анализа в детерминированном экономическом анализе наиболее полно решает проблему получения однозначно определяемых величин влияния факторов. [c.134]
Выше было установлено, что любую модель конечной факторной системы можно привести к двум видам — мультипликативной и кратной. Это условие предопределяет то, что исследователь имеет дело с двумя основными видами моделей факторных систем, так как остальные модели — это их разновидности. [c.134]
Для облегчения решения задачи построения подынтегральных выражений в зависимости от вида модели факторной системы (мультипликативные или кратные) предложим матрицы исходных значений для построения подынтегральных выражений элементов структуры факторной системы. Принцип, заложенный в матрицах, позволяет построить подынтегральные выражения элементов структуры факторной системы для любого набора элементов модели конечной факторной системы. В основном построение подынтегральных выражений элементов структуры факторной системы — процесс индивидуальный, и в случае, когда число элементов структуры измеряется большим количеством, что в экономической практике является редкостью, исходят из конкретно заданных условий. [c.134]
При формировании рабочих формул расчета влияния факторов в условиях применения ЭВМ пользуются следующими правилами, -отражающими механику работы с матрицами подынтегральные выражения элементов структуры факторной системы для мультипликативных моделей строятся путем произведения полного набора элементов значений, взятых по каждой строке матрицы, отнесенных к определенному элементу структуры факторной системы с последующей расшифровкой [c.134]
Элементы мультипликативной модели [c.135]
В случае отсутствия универсальных вычислительных средств предложим чаще всего встречающийся в экономическом анализе набор формул расчета элементов структуры для мультипликативных (табл. 5.4) и кратных (табл. 5.3) моделей факторных систем, которые были выведены в результате выполнения процесса интегрирования. Учитывая потребность наибольшего их упрощения, выполнена вычислительная процедура по сжатию формул, полученных после вычисления определенных интегралов (операции интегрирования). [c.138]
Набор частных свойств специфичен, как и формы их синтеза. В большинстве случаев отдельные свойства коррелируют, что обусловливает т.н. мультипликативный эффект взаимоусиления (чаще) или взаимовлияния на полезность (качество) изделия. Поэтому приближенный к истине при отсутствии теоретически обоснованной модели является способ выражения интегрального показателя качества функцией вида [c.124]
Алгоритм расчета для мультипликативной четырехфакторнон модели валовой продукции выглядит следующим образом [c.58]
Интегральный метол применяется для измерения влияния факторов в мультипликативных, кратных и кратно-а 1дитии ых моделях. Его использование позволяет получать более точные результаты расчета влияния факторов по сравнению со способами г пной подстановки, абсолютных и относительных разниц, поскольку дополнительный прирост результативного показателя от взаимодействия факторов присоединяется не к последнему фактору, а делится поровну между ними. [c.61]
Способ логарифмирования применяется для измерения влияния факторов в мультипликативных моделях. Как п при интегрировании, здесь результат расчета также не зависит от месторасположения факторов в модели. По сравнению с интегральным методом логарифмирование обеспечивает более высокую точность расчетов. Если при интегрировании дополнительный прирост от взаимодействия факторов распределяется поровну между ними, то с помощью логарифмирования результат совместного действия факторов распределяется пропорционально доли изолированного влияния каждого фактора на уровень результативного показателя. В тгом его преимущество, а недостаток — в ограниченности сферы применения. [c.63]
При построении моделей себестоимости добычи нефти и газа по НГДУ Прикарпатья (линейная, полином третьей степени мультипликативная функция Кобба — Дугласа) ни одна из них не выдержала проверки на адекватность (табл. 29). Величины критериев, характеризующих экономико-статистическую достоверность кинетической производственной функции по нефтегазодобывающим управлениям Прикарпатья, приведены в табл. 30. [c.94]
Построенные многофакторные корреляционные модели по нефте-х добывающей промышленности Украины, нефтегазодобывающим управлениям Прикарпатья, НГДУ Долинанефтегаз вида множественной линейной функции, мультипликативной функции Кобба — Дугласа, кинетической производственной функции позволили сделать количественную оценку влияния различных факторов в их взаимосвязи на динамику себестоимости добычи нефти и попутного газа. Исследована специфика экономико-математического моделирования в нефтедобывающей промышленности, и с этих позиций обосновано использование в качестве функции себестоимости добычи нефти и газа кинетической трансцендентной функции вида [c.111]
Как видно, метод взвешенных конечных разностей учитывает все варианты подстановок. Одновременно при усреднении нельзя получить однозначное количественное значение отдельных факторов. Этот метод весьма трудоемкий и по сравнению с предыдущим методом усложняет вычислительную процедуру, так как приходится перебирать все возможные варианты подстановок. В своей основе метод взвешенных конечных разностей идентичен (только для двухфактор-ной мультипликативной модели) методу простого прибавления неразложимого остатка при делении этого остатка между факторами поровну. Это подтверждается следующим преобразованием формулы [c.124]
В более общем виде этот метод был описан еще А. Хума-лом, который писал Такое разделение прироста произведения может быть названо нормальным. Название оправдывается тем, что полученное правило разделения остается в силе при любом числе сомножителей, а именно прирост произведения разделяется между переменными сомножителями пропорционально логарифмам их коэффициентов изменения [69, с. 207]. Действительно, в случае наличия большего числа сомножителей в анализируемой мультипликативной модели факторной системы (например, z = хурт) суммарное приращение результативного показателя Az составит [c.125]
Вид моделей факторной системы /= xyzq (мультипликативная модель). [c.135]
Смотреть страницы где упоминается термин Модель мультипликативная
: [c.134] [c.441] [c.442] [c.209] [c.34] [c.270] [c.271] [c.106] [c.107] [c.135]Эконометрика (2001) -- [ c.226 , c.240 , c.245 , c.246 , c.247 , c.248 , c.249 ]
