Конечно, чем больше требуемые фонды, тем больше общая потребность в финансировании. Но в то же время природа фондов обусловливает наиболее подходящий тип финансирования. Если для данной фирмы немаловажна, например, сезонная компонента, то это обстоятельство диктует большую предпочтительность краткосрочных кредитов банков. Также существенную роль для выбора вида финансирования играет бизнес-риск. Чем он выше, тем менее желательно финансирование путем получения займов по сравнению с выпуском акций. Другими словами, выпуск новых акций безопаснее, поскольку он не предполагает выплаты процентов на привлеченный капитал. Фирме с высокой степенью бизнес-риска обычно не рекомендуют брать на себя дополнительно значительные финансовые риски. При выборе вида финансирования следует также оценить общее финансовое состояние фирмы. Чем оно прочнее, тем выше рентабельность и ликвидность, тем на больший риск можно пойти при выборе вида финансирования. Поэтому получение займов становится тем более предпочтительным, чем лучше перечисленные выше показатели. [c.140]
Как уже отмечено выше, одной из важнейших задач исследования экономического временного ряда является выявление основной тенденции изучаемого процесса, выраженной неслучайной составляющей Д/) (тренда либо тренда с циклической или (и) сезонной компонентой). [c.139]
Подобное предположение, приводящее к значительным техническим упрощениям, может быть оправдано в том случае, когда экспериментальные данные представляют собой пространственную выборку. В самом деле, мы можем считать, что значения переменных Xj мы выбираем заранее, а затем наблюдаем получающиеся при этом значения Y (здесь имеется некоторая аналогия с заданием функции по точкам — значения независимой переменной выбираются произвольно, а значения зависимой вычисляются). В случае временного ряда, регрессоры которого представляют собой временной тренд, циклическую и сезонную компоненты, объясняющие переменные также, очевидно, не случайны. [c.191]
На основе помесячных данных о числе браков (тыс.) в регионе за последние три года была построена аддитивная модель временного ряда. Скорректированные значения сезонной компоненты за соответствующие месяцы приводятся в табл. 4.6. [c.149]
Месяц Скорректированные значения сезонной компоненты Месяц Скорректированные значения сезонной компоненты [c.149]
Определить значение сезонной компоненты за декабрь. [c.149]
Сумма значений сезонной компоненты внутри одного цикла должна быть равна нулю (в соответствии с методикой построения аддитивной модели временного ряда). Следовательно, значение сезонной компоненты за декабрь составит [c.149]
Прогнозное значение уровня временного ряда F, в аддитивной модели есть сумма трендового значения Т, и соответствующего значения сезонной компоненты 5,. [c.149]
Соответствующие значения сезонных компонент составят [c.150]
Рассчитайте трендовую и сезонную компоненты. [c.168]
На основе поквартальных данных об уровне безработицы в летнем курортном городе (% от экономически активного населения) за последние 5 лет была построена мультипликативная модель временного ряда. Скорректированные значения сезонной компоненты за каждый квартал приводятся ниже [c.170]
Определите значения сезонной компоненты за IV квартал. [c.170]
Исходя из структуры уровней временного ряда, которые включают тренд (7), конъюнктурный цикл (К), сезонную компоненту (5) и остаточную компоненту (К), можно представить любой динамический ряд как сумму четырех названных составляющих. Так, временные ряды показателей X и Y можно записать следующим образом [c.19]
Во-вторых, изучаемый показатель может быть подвержен циклическим колебаниям. Эти колебания могут носить сезонный характер, поскольку экономическая деятельность ряда отраслей экономики зависит от времени года (например, цены на сельскохозяйственную продукцию в летний период выше, чем в зимний уровень безработицы в курортных городах в зимний период выше по сравнению с летним). При наличии больших массивов данных за длительные промежутки времени можно выявить циклические колебания, связанные с общей динамикой конъюнктуры рынка, а также с фазой-бизнес цикла, в которой находится экономика страны. На рис. 5.1 6) представлен гипотетический временной ряд, содержащий только сезонную компоненту. [c.226]
Если наиболее высоким оказался коэффициент автокорреляции первого порядка, исследуемый ряд содержит только тенденцию. Если наиболее высоким оказался коэффициент автокорреляции порядка г, ряд содержит циклические колебания с периодичностью в г моментов времени. Если ни один из коэффициентов автокорреляции не является значимым, можно сделать одно из двух предположений относительно структуры этого ряда либо ряд не содержит тенденции и циклических колебаний и имеет структуру, сходную со структурой ряда, изображенного на рис. 5.1 в), либо ряд содержит сильную нелинейную тенденцию, для выявления которой нужно провести дополнительный анализ. Поэтому коэффициент автокорреляции уровней и автокорреляционную функцию целесообразно использовать для выявления во временном ряде наличия или отсутствия трендовой компоненты (7) и циклической (сезонной) компоненты (S). [c.231]
Простейший подход — расчет значений сезонной компоненты методом скользящей средней и построение аддитивной или мультипликативной модели временного ряда. Общий вид аддитивной модели следующий [c.239]
Эта модель предполагает, что каждый уровень временного ряда может быть представлен как произведение трендовой (7), сезонной (S) и случайной ( ) компонент. Выбор одной из двух моделей осуществляется на основе анализа структуры сезонных колебаний. Если амплитуда колебаний приблизительно постоянна, строят аддитивную модель временного ряда, в которой значения сезонной компоненты предполагаются постоянными для различных циклов. Если амплитуда сезонных колебаний возрастает или уменьшается, строят мультипликативную модель временного ряда, которая ставит уровни ряда в зависимость от значений сезонной компоненты. [c.240]
Расчет значений сезонной компоненты S. [c.240]
Устранение сезонной компоненты из исходных уровней ряда и получение выравненных данных (Т+ Е) в аддитивной или (Г- Е)ъ мультипликативной модели. [c.240]
| Таблица 5.8 Расчет оценок сезонной компоненты в аддитивной модели |  |
Скорректированная сезонная компонента, St 0,581 -1,977 -1,294 2,690 [c.242]
Рассчитаем скорректированные значения сезонной компоненты как разность между ее средней оценкой и корректирующим коэффициентом к [c.242]
Проверим условие равенства нулю суммы значений сезонной компоненты [c.243]
Таким образом, получены следующие значения сезонной компоненты [c.243]
Шаг 3. Элиминируем влияние сезонной компоненты, вычитая ее значение из каждого уровня исходного временного ряда. Получим величины Т + Е= Y-S (гр. 4 табл. 5.10). Эти значения рассчитываются за каждый момент времени и содержат только тенденцию и случайную компоненту. [c.243]
Шаг 5. Найдем значения уровней ряда, полученные по аддитивной модели. Для этого прибавим к уровням Г значения сезонной компоненты для соответствующих кварталов. Графически значения (Т+ S) представлены на рис. 5.5. [c.244]
Шаг 1. Проведем выравнивание исходных уровней ряда методом скользящей средней. Методика, применяемая на этом шаге, полностью совпадает с методикой аддитивной модели. Результаты расчетов оценок сезонной компоненты представлены в табл. 5.12. [c.246]
| Таблица 5.12 Расчет оценок сезонной компоненты в мультипликативной модели | 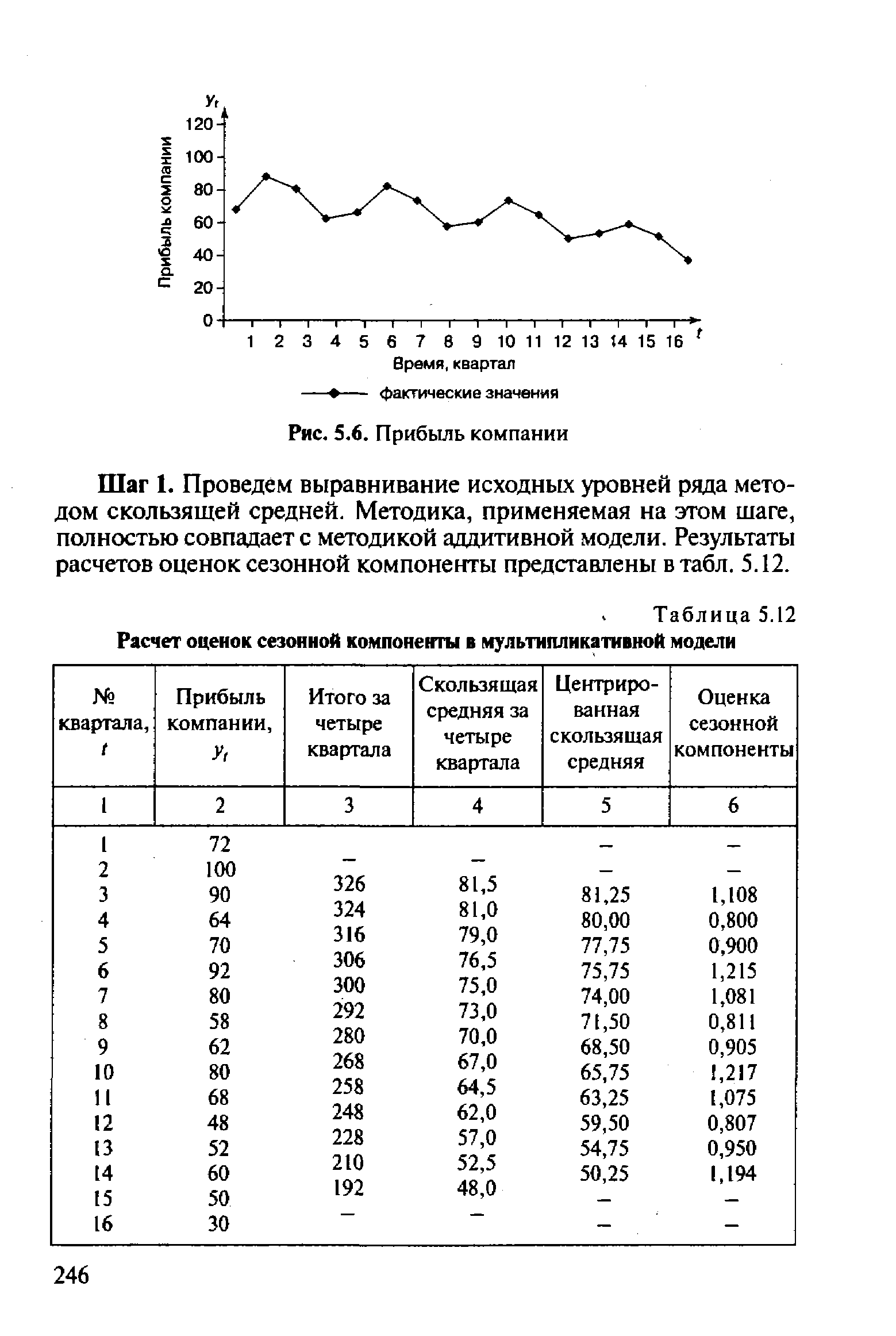 |
Скорректированная сезонная компонента, Sf 0,913 1,202 1,082 0,803 [c.247]
Определим скорректированные значения сезонной компоненты, умножив ее средние оценки на корректирующий коэффициент к. [c.247]
Получим следующие значения сезонной компоненты [c.248]
Шаг 2. Найдем оценки сезонной компоненты как разность между фактическими уровнями ряда и центрированными скользящими средними (гр. 6 табл. 5.8). Используем эти оценки для расчета значений сезонной компоненты S (табл. 5.9). Для этого найдем средние за каждый квартал (по всем годам) оценки сезонной компоненты Sf. В моделях с сезонной компонентой обычно предполагается, что сезонные воздействия за период взаимопогашаются. В аддитивной модели это выражается в том, что сумма значений сезонной компоненты по всем кварталам должна быть равна нулю. [c.242]
Шаг 2. Найдем оценки сезонной компоненты как частное от деления фактических уровней ряда на центрированные скользящие средние (гр. 6 табл. 5.12). Используем эти оценки для расчета значений сезонной компоненты S (табл. 5.13). Для этого найдем средние за каждый квартал оценки сезонной компоненты 51,-. Взаимопогашаемость сезонных воздействий в мультипликативной модели выражается в том, что сумма значений сезонной компоненты по всем кварталам должна быть равна числу периодов в цикле. В нашем случае число периодов одного цикла (год) равно 4 (четыре квартала). [c.247]
