Развитие теории производственной функции связывается с производственной функцией Кобба — Дугласа. Эти авторы (США) проанализировали статистические данные американской промышленности за период 1899—1922 гг. и обосновали использование в экономическом анализе мультипликативной функции, носящей теперь их имя. [c.79]
Мультипликативная функция Кобба — Дугласа [c.84]
Корреляционная модель себестоимости добычи нефти и попутного газа по указанным факторам была рассчитана по мультипликативной функции Кобба — Дугласа (41). В результате решения этой модели было составлено сводное уравнение по нефтедобывающей промышленности Украинской ССР [c.90]
Мультипликативная функция Коб-ба — Дугласа . ......... 0,00828 0,9246 0,939 [c.95]
Остановимся подробнее на методике комплексного использования методов. Рассмотрим простейший случай. Пусть изучаемый результативный признак может быть представлен как жестко детерминированная двухфакторная мультипликативная функция у = xw (несмотря на то, что оба фактора х и w принадлежат одному и тому же уровню изучаемой структуры, мы обозначили их по-разному для того, чтобы облегчить изложение методических вопросов). Пусть х -первичный (объемный) признак, w - вторичный (так называемый количественный) признак. Тогда система аналитических индексов имеет вид [c.410]
Теперь возведем уравнение (1.16а) или (1.166) в степень N, чтобы рассчитать TWR Оно будет близко к мультипликативной функции роста, действительному TWR [c.52]
Теперь для для получения оценки TWR возведем уравнения [1.07] и [1.10а,Ь] в степень Т. Эта оценка будет весьма точно аппроксимировать мультипликативную функцию роста, или настоящее TWR, из формулы [1.06] [c.57]
При всех отмеченных выше недостатках проводимого анализа, учитывающего только основные выделенные блоки и связи экономической системы, представляется, что именно абстрагирование от частностей может позволить выявить основные механизмы реальной экономики, представляя их в обобщенном виде, очищенном от наслоений повседневной турбулентности реальной экономической конкретики. При этом полиномиальный характер зависимости от времени в формуле (4.5.9) представляет собой наиболее естественную форму общих моделей развития, широко используемую, в том числе, в экономических исследованиях. Новым фактом является, следовательно, только конкретизация конструкции коэффициентов разложения, как мультипликативных функций от инвестиций, позволяющая выявить принципы их согласованной работы в блоках экономики в рассматриваемой здесь общей задаче развития Производства. [c.371]
Полиномиальный характер роста реальных экономических процессов впервые был выделен и изучен Н. Д. Кондратьевым в знаменитой работе Большие циклы конъюнктуры 1925 г. [Кондратьев, 1993]. Там было показано, что систематический рост изученных им экономических показателей капиталистических стран может быть описан полиномами разных степеней по времени. Сопоставляя закон роста (4.5.9) с данными Н. Д. Кондратьева, можно предположить, что этот закон конкретизирует конструкции коэффициентов общей теоретической формы полиномиальных рядов экономического роста. Структура коэффициентов как мультипликативных функций [c.371]
Иногда допустимой может считаться не абсолютная, а относительная компенсация изменения значений одних критериев другими, т. е. ЛПР согласно с тем, что суммарная степень относительного снижения одних критериев эквивалентна суммарному уровню относительного увеличения остальных. Это приводит к мультипликативной функции агрегирования т - [c.196]
Если мы вспомним (см. п. 2.5), что мультипликативная функция моделирует некоторую допустимую компенсацию [c.251]
Слагаемые аддитивной целевой функции соответствуют эффекту решений, принимаемых на отдельных этапах управляемого процесса. По аналогии, мультипликативная функция распадается на произведение положительных функций различных переменных [c.159]
Аддитивная и мультипликативная функция. [c.183]
Применив логику изложенного выше цепного (т. е. поэтапно осуществляемого) индексного метода, приходим к простому решению по-факторного разложения прироста показателя В, являющегося мультипликативной функцией трех факторов [c.325]
| Таблица 3 Мультипликативная производственная функция Кобба — Дугласа | 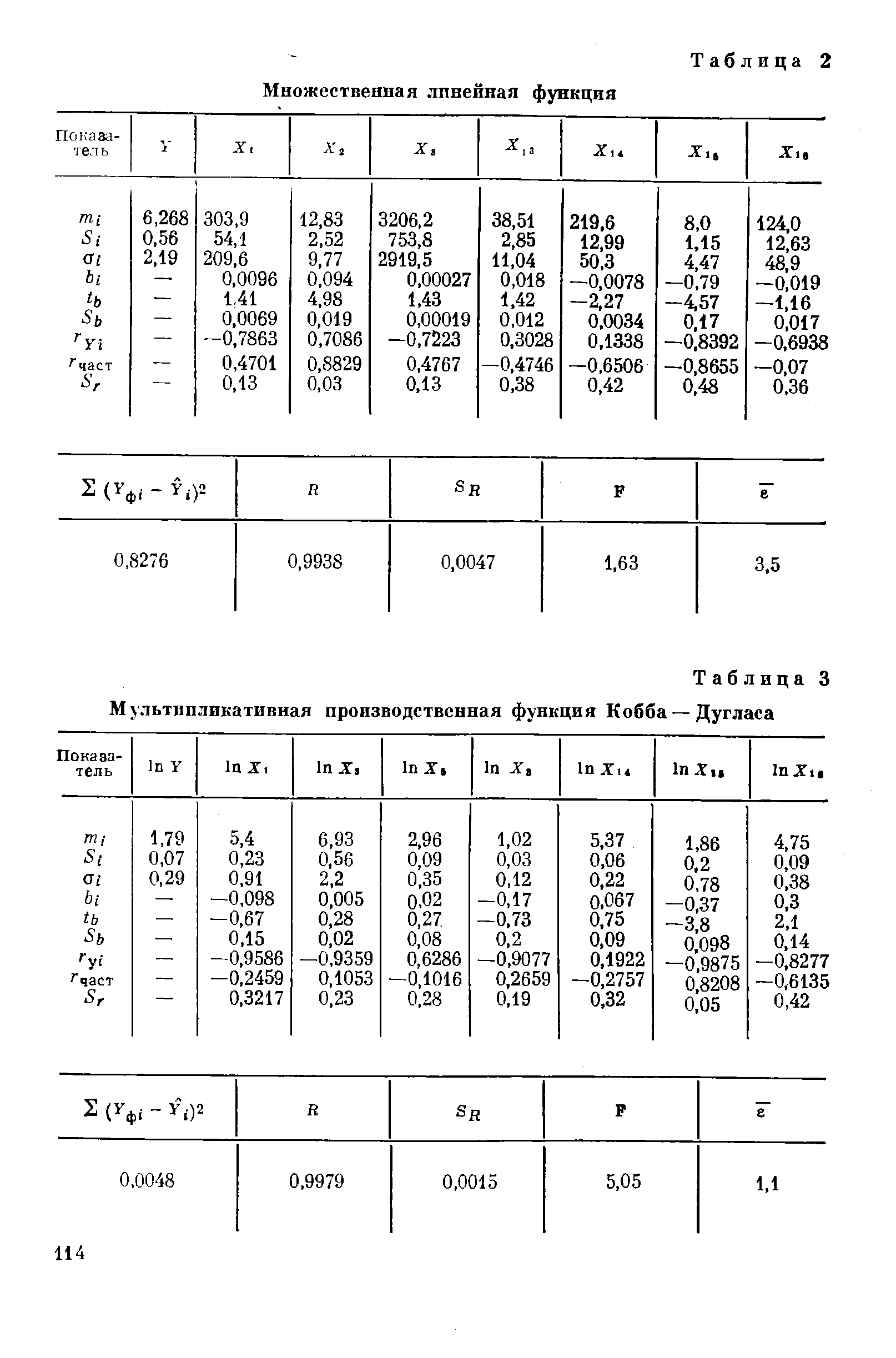 |
Q мультипликативные модели, функция является произведением факторов с некоторым коэффициентом [c.432]
Общий вид зависимости оценки стандартного отклонения sn от п приводится на рис. 4.2.2. Как можно заметить из рис. 4.2.2, в графике функции sn(n) присутствует некоторая точка перегиба га, определяющая номер периода, начиная с которого скорость расхождения границ доверительного интервала качественно возрастает. Последний факт может быть использован для определения того количества периодов, на которое мы в рамках мультипликативной модели можем получить относительно осмысленную оценку границ отклонений фактических значений от прогнозных. [c.158]
Разновидностью приема цепных подстановок является способ расчёта с помощью абсолютных разниц. Целевая функция при этом, так же как и в предыдущем примере, представлена в виде мультипликативной модели. Определяется изменение величины каждого фактора по сравнению с базовым значением, например, плановым. Затем эти разности умножают на остальные частные показатели — множители мультипликативной модели. Но, заметим, при переходе от одного фактора к другому берётся в расчёт уже другое значение множителя. Множители, стоящие после того фактора (справа), по которому рассчитывается разница, остаются в значении базового периода, а все оставшиеся перед ним (слева), берутся в значениях отчётного периода. [c.61]
Уравнение (1.04) можно прокомментировать следующим образом. Если HPR = О, то вы полностью выйдете из игры, так как все, что умножается на ноль, равно нулю. Любая большая проигрышная сделка будет иметь самое неблагоприятное влияние на TWR, так как эта функция. мультипликативна, а не аддитивна. [c.31]
Другая вредоносная идея — это временное взвешивание дополнения средств на счете и частичного их изъятия. Временное взвешивание широко практикуется в сфере управления капиталами, несмотря на то, что из-за свойственной ему недооценки фактических итогов, оно действует против менеджеров. Обычно при временном взвешивании требуется, чтобы итоги вычислялись как функция от количества дней за период (как правило, за месяц), в течение которых деньги были доступны. То есть если некто открывает счет на шестнадцатый день 30-дневного месяца, то деньги будут доступны для менеджера половину (0,5) этого месяца. Итоги по данному счету за весь месяц будут далее умножены на 2. Так, если в том месяце по данному счету был получен доход в 10%, то в качестве итога будет показано 20%. Аналогично, при потере 10% будет показана итоговая потеря 20%. Пусть прямолинейная экстраполяция и довольно надуманна, она должна применяться здесь не в аддитивном, а в мультипликативном смысле. Другими словами, доход в 10% нашего примера, будучи экстраполирован на оставшуюся часть месяца, должен бы составить 1,1 1,1 = 1,21, или 21% дохода. Аналогичным образом, потеря в 10% в данном случае должна бы представляться, как 0,9 0,9 = 0,81, или потерю в 19% за месяц. [c.93]
Соответственно оценки параметров аи b могут быть найдены МНК. В рассматриваемой степенной функции предполагается, что случайная ошибка е мультипликативно связана с объясняющей переменной х. Если же модель представить в виде у = а х + е, то она становится внутренне нелинейной, ибо ее невозможно превратить в линейный вид. [c.70]
Двухфакторная мультипликативная модель - функция вида [c.59]
Предположим теперь, что функция (y-h) является мультипликативной, то [c.23]
Мультипликативная форма представления функции [c.208]
Э.м. находит отражение в структуре мультипликативно-степенной производственной функции вида [c.429]
При построении моделей себестоимости добычи нефти и газа по НГДУ Прикарпатья (линейная, полином третьей степени мультипликативная функция Кобба — Дугласа) ни одна из них не выдержала проверки на адекватность (табл. 29). Величины критериев, характеризующих экономико-статистическую достоверность кинетической производственной функции по нефтегазодобывающим управлениям Прикарпатья, приведены в табл. 30. [c.94]
Построенные многофакторные корреляционные модели по нефте-х добывающей промышленности Украины, нефтегазодобывающим управлениям Прикарпатья, НГДУ Долинанефтегаз вида множественной линейной функции, мультипликативной функции Кобба — Дугласа, кинетической производственной функции позволили сделать количественную оценку влияния различных факторов в их взаимосвязи на динамику себестоимости добычи нефти и попутного газа. Исследована специфика экономико-математического моделирования в нефтедобывающей промышленности, и с этих позиций обосновано использование в качестве функции себестоимости добычи нефти и газа кинетической трансцендентной функции вида [c.111]
Таким образом, интегральный показатель 7 задается мультипликативной функцией R=11RK / с Як (О Я 1), а гру п-п о в ы е ( гр) определяются как взвешенные суммы частных показателей шг rt [c.52]
Согласно экономическому принципу, за все хорошее набо платить, необходимость увеличения надежности часто приводит к снижению доходности и наоборот. Иными словами, состояние кредитных отношений характеризуется обратной зависимостью этих двух параметров. Тогда состояние кредитного договора можно представить индексом состояния кредита (ИСК) как произведение (мультипликативную функцию) равноправных составляющих (надежности и доходности) [c.113]
Набор частных свойств специфичен, как и формы их синтеза. В большинстве случаев отдельные свойства коррелируют, что обусловливает т.н. мультипликативный эффект взаимоусиления (чаще) или взаимовлияния на полезность (качество) изделия. Поэтому приближенный к истине при отсутствии теоретически обоснованной модели является способ выражения интегрального показателя качества функцией вида [c.124]
Наоборот, если у - объем валовой продукции завода, , - число работников, дг2 - стоимость основных производственных фондов, 3 -затраты на энергию, топливо, сырье и материалы (комплектующие изделия), то результат без любого из факторов не существует, поэтому большинство экономистов-статистиков строят КРМ (называемую производственной функцией, что весьма неудачно терминологически) в мультипликативной форме [c.287]
Представление (11.14) описывает грехфакторную жестко детерминированную мультипликативную модель. Согласно этой модели величина товарных запасов может быть представлена как функция трех параметров то- [c.450]
МУЛЬТИПЛИКАТИВНАЯ ФОРМА ПРЕДСТАВЛЕНИЯ ФУНКЦИИ [-multipli ative fun tion] — представление функции нескольких переменных в виде их произведения используется для формализованной записи, напр. при моделировании взаимодействия разных факторов (см. Производственная функция), где отсутствие любого из них обращает функцию выпуска в нуль, а также в некоторых моделях управления, где воздействие ошибок не взаимопогашается (элиминируется), а усиливается. Для сокращенной записи используется знак П (см. Произведение). [c.208]
В различных экономических приложениях применяются (и рассматриваются в словаре) следующие функции Взвешивающие, Дифференцируемые, Гладкие, Кусочно-линейные, Кусочно-непрерывные, Линейные, Нелинейные, Непрерывные, Се-парабелъные, Экспоненты и др. См. также Вектор-функция, Гессиан, Интеграл, Мультипликативная форма представления функции, Производная, Рекурсия, Частная производная, Эластичность функции. [c.379]
Монопсоническая власть (сила) 207 Монопсония 207 Монотонная функция 207 Монотонное преобразование 207 Монотонные функции полезности 380 Монте-Карло метод (метод статистических испытаний) 195 Морфологический анализ 207 Мощность аклератора 14 Мощность кода 146 Мультиколлинеарность 207 Мультимодальное распределение 202 Мультипликативная форма представления [c.475]
