Пусть F(U(x)) будет любым положительным монотонным преобразованием [c.75]
Формула, данная через U x), представляет отношение к риску, не варьирующееся по отношению к положительному монотонному преобразованию, если сохраняется абсолютная и относительная нерасположенность к риску. Необходимым и достаточным условием для этого является постоянство коэффициента Эрроу—Пратта [c.75]
П. из множества действительных чисел называется числовой последовательностью. См. также Монотонное преобразование, Упорядочение. [c.269]
I. Монотонное преобразование критерия, при котором задача (9.8) преобразуется в задачу [c.312]
III. Монотонное преобразование суммы критерия оптимальности с исчезающим слагаемым [c.312]
Расширение Лагранжа в комбинации с монотонным преобразованием целевой функции. Рассмотрим задачу, тождественную по решению задаче НП вида [c.347]
Отметим, что монотонное преобразование целевой функции реализуется, по существу, и в методе уровней (см., например, [19]). [c.348]
| Рис. 9.11. Пример монотонного преобразования функции достижимости, превращающего ее в выпуклую | 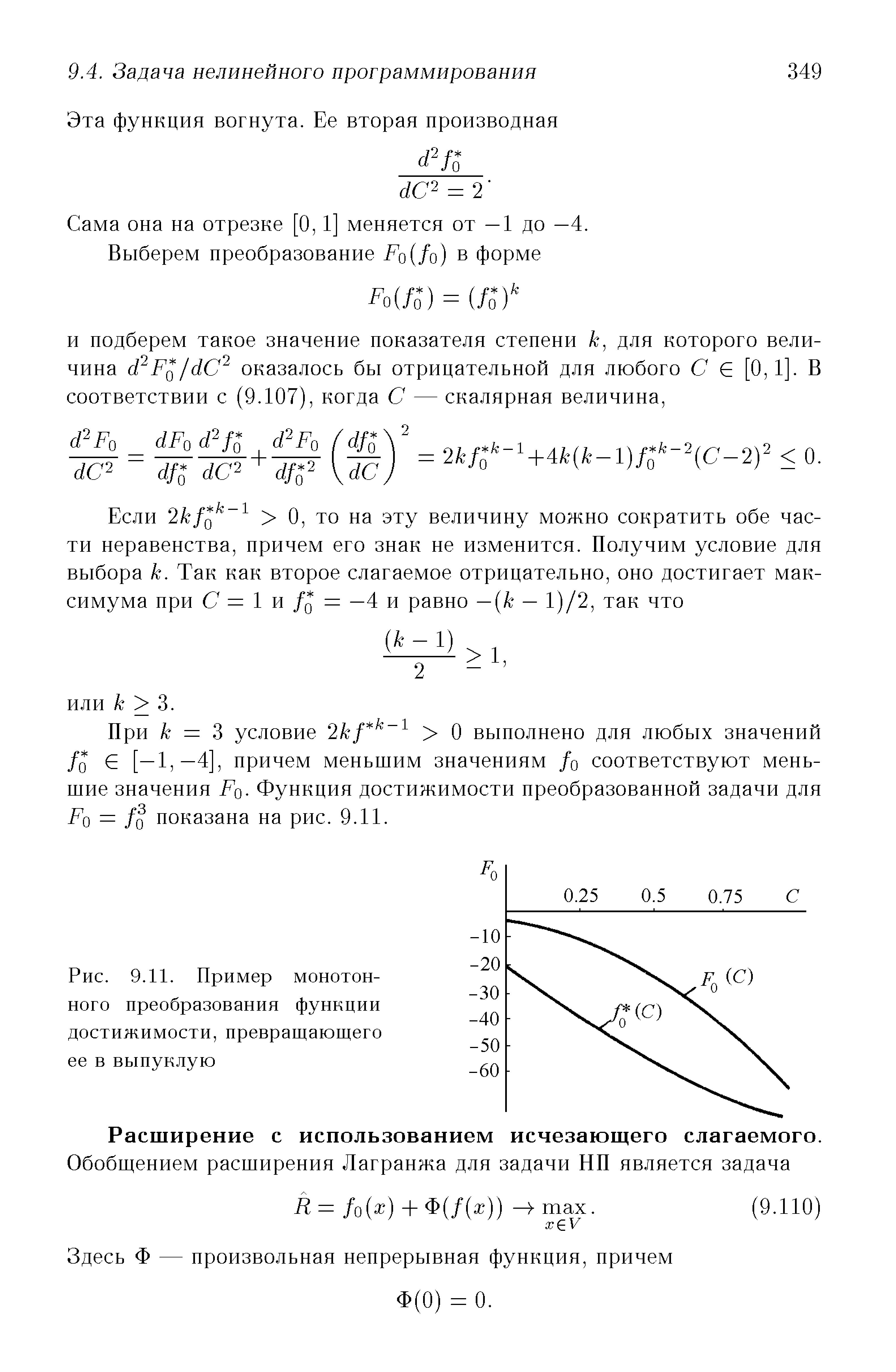 |
Б. Монотонные преобразования целевой функции с ведением квадратичного штрафа. [c.358]
Мы начнем с монотонных преобразований, а затем перейдем к линейным преобразованиям, разобрав два частных случая — постоянного множителя и добавочной константы. [c.338]
Давайте зададим числовые значения каждой рассматриваемой категории. Например, в таблице I для десяти сущностей от А до /, находящихся в крайней левой колонке, имеется девять различных наборов чисел, используемых для того, чтобы задать девять различных чисел для каждой из них. Если два ряда чисел (мер) дают один и тот же порядок ранжирования или упорядочения сущностей (в соответствии с приписанными числами), то в этом случае эти два ряда являются монотонными преобразованиями друг друга. [c.338]
В таблице I можно видеть, что все девять мер дают то же самое ранжирование, поэтому все девять мер являются монотонными преобразованиями друг друга. Если это свойство распространяется на весь класс рассматриваемых сущностей, тогда эти две меры являются монотонными преобразованиями друг [c.338]
Приступим к линейному преобразованию с рассмотрения двух особых форм. Посмотрите на числа в колонке 3. Они те же самые, что и в колонке 1, только добавлена некая константа, в данном случае 5, т. е. они те же самые с точностью до (за исключением) какой-то добавочной константы. Числа в колонке 4 эквивалентны соответственно числам в колонке 1 с добавлением 10. Колонки 1, 3 и 4 являются результатом преобразования друг друга с точностью до (посредством) добавочной константы. Можно также сказать, что они эквивалентны, за исключением добавочной константы.Термин с точностью до означает, что мы можем рассматривать некоторые более простые типы. Например, все преобразования до какой-то добавочной константы содержатся также в более широком, менее ограниченном классе возможных преобразований, известном как монотонные преобразования. Добавочная константа является довольно сильным ограничением, даже если это и не видно с первого взгляда, т. к. существует неограниченное количество имеющихся в распоряжении констант. Однако относительный диапазон возможностей в общих линейных преобразованиях на самом деле очень ограничен. [c.339]
А теперь посмотрим на колонку 5. Она эквивалентна колонке 1 за исключением того, что числа колонки 1 умножаются на константу, в данном случае 2. Колонка 5 является монотонным преобразованием колонки 1, и это также некое преобразование чисел колонки 1, умножение на константу . Колонка 6 — это числа колонки 1, умноженные на 6. Таким образом, хотя колонки 1, 5 и 6 являются монотонными преобразованиями друг друга, они являются также более частным видом преобразования. Они являются преобразованиями с точностью до какого-то постоянного множителя. Эти случаи являются частными случаями линейных преобразований, которые мы сейчас обсудим. [c.340]
В монотонных преобразованиях только знак разностей первого порядка остается без изменений. [c.341]
Необходимо только определить, правильным ли будет порядок то, что порядок является тем же самым, независимо от того, какое из вышеупомянутых преобразований используется, не означает, что порядок является правильным. Что мы подразумеваем под правильным Мы имеем в виду, что наш установленный или прогнозируемый порядок согласован с порядком, выявленным в любом другом наблюдаемом процессе упорядочения. Можно было бы поставить сущности на какие-либо новые весы (новые весы — это испытание ), и тогда сопоставление порядка, полученного с помощью новых весов, с нашим установленным порядком будет являться проверкой правильности (прогнозируемой достоверности) нашего первого порядка. Любое монотонное преобразование одной значимой последовательности упорядоченных чисел является для цели этой иллюстрации полностью эквивалентным для фактически используемых чисел. То есть любое из возможных монотонных преобразований является справедливым, в равной степени как и любое другое. [c.342]
Мы можем суммировать, сказав, что при наличии системы для действительно упорядоченных сущностей, любое монотонное преобразование частных числовых значений, заданных в процессе упорядочения, будет в равной мере удовлетворительным. Формально мы можем сказать, что все показатели порядка эквивалентны с точностью до (за исключением имеющихся) монотонных преобразований . Или другими словами, метод, в действительности указывающий только порядок, не может быть однозначно принят, как правильный для какого-то частного множества чисел. Любое монотонное преобразование будет действовать точно так же. Степень однозначности упорядочения может быть охарактеризована следующим образом упорядочение является однозначным исключительно как ряд монотонных преобразований. Поэтому мы часто встречаем выражение упорядочение является однозначным вплоть до монотонного преобразования . [c.342]
Предположим, что цель у нас другая. Предположим, что мы хотим иметь возможность расположить по порядку группы сущностей в соответствии с их значимостью. А точнее, предположим, что мы хотим приписать числа для каждого из составляющих объектов таким образом, что когда мы соединим объекты в множества или наборы, мы сможем расположить по порядку значимость этих наборов, зная только отдельно числа, приписанные каждой компоненте, путем простого сложения чисел, заданных для каждой компоненты. И мы хотим, чтобы это можно было сделать для любой возможной комбинации объектов. К счастью, люди нашли способ сделать это для взвешивания. Числа, которые задаются в результате этого процесса, являются произвольно выбранными вплоть до какого-то постоянного множителя (или пропорции) так, чтобы эти числа могли выражать фунты или унции, тонны или граммы. То есть мы можем произвольно умножать все числа, приписанные различным компонентам, на любую желаемую константу, не нарушая достоверности наших результирующих чисел для данной определенной цели. Но никакое монотонное преобразование мы использовать не можем, как могли это делать в предыдущем случае, где наша цель была другой. [c.343]
Благодаря указанному методу определения полезностей мы упорядочили все сущности. Однако наша цель больше этого иначе однозначность чисел с точностью до линейного преобразования будет излишним ограничением. Как известно, любое монотонное преобразование оставит порядок неизменным. Это ограничение линейного преобразования вызвано нашим желанием прогнозировать выбор среди неопределенных перспектив, исходя из полезностей и вероятностей составных сущностей, и делать это подобающим образом, то есть соответственно максимизации ожидаемой полезности.1 [c.355]
Если наша задача состоит просто в том, чтобы упорядочить выбор среди неопределенных перспектив, мы могли бы после получения ожидаемой полезности этой перспективы, очевидно, произвести в ней любое монотонное преобразование, не нарушая порядка выбора среди этих неопределенных перспектив. Однако не имеет [c.356]
Теперь наш обзор закончен. Мы начали с разработок положения полезности по Слуцкому, Хиксу, Аллену, в которых полезность измеряется только с точностью до монотонных преобразований. Это подразумевает ни больше и ни меньше, а именно то, что полезность является порядковой. Другими словами, численная величина приращения в этих числах на какую-то одну единицу [c.363]
Вначале остановимся на некоторых важных свойствах задачи потребительского выбора. Во-первых, решение задачи (х,°,д 0) сохраняется при любом монотонном (то есть сохраняющем порядок значений) преобразовании функции полезности ы(х,,л ). Поскольку значение (х,0 0) было максимальным на всем допустимом множестве, оно остается таковым и после монотонного преобразования функции полезности (допустимое множество, определяемое бюджетным ограничением, остается неизменным). Таким монотонным преобразованием может быть умножение функции полезности на некоторое положительное число, возведение ее в положительную степень, логарифмирование по основанию, большему единицы. Отметим, что свойство 1) должно присутствовать у любой функции полезности свойства 2) и 3) могут при ее монотонных преобразованиях теряться или приобретаться (рассмотрите это самостоятельно на примере функции uix xj x x., . Последнее важно для иллюстрации того [c.140]
Другой способ определения функции F, отличный от способа суперпозиции, состоит в том, что при применении какого-либо квантификатора к другому квантификатору происходит некое монотонное преобразование исходной функции принадлежности, сводящееся к растяжению и сдвигу максимума функции в ту или другую сторону. [c.145]
Замечание На самом деле достаточно, чтобы данная функция полезности могла быть преобразована в вогнутую каким-либо монотонным (строго возрастающим) преобразованием. Монотонное преобразование функции полезности не меняет предпочтений потребителя. Так, например, функция ы(ж, у) =ху и ее логарифм 1п(ы(ж, у)) = 1п(ж) + 1п(у) задают одни и те же потребительские предпочтения, хотя первая не вогнута, а вторая вогнута и допускает поэтому применение теоремы Куна — Таккера. Следовательно, допускает его и первая, приводимая к вогнутой. [c.158]
Рассмотрим вопрос о том, как изменяются свойства функции затрат при монотонном преобразовании типов активных элементов. Ответ на этот вопрос дает следующая лемма. [c.34]
Монотонное преобразование функции полезности. [c.16]
Монотонное преобразование функции полезности - это новая функция полезности, которая точно также описывает предпочтения потребителя (то есть показывает более или менее предпочтителен тот или иной набор благ), как и первоначальная функция полезности. Пусть, например, существует отношение предпочтения х>у (х,у Х). Тогда функция полезности U, по определению, должна отражать это предпочтение следующим образом t/(x) > U(y ). Однако, если [c.16]
Естественно, мы можем анализировать и каждое линейно положительное монотонное преобразование (2.23) U (x) = z + yU(x) = z — yax2 + уЫ, причем необходимо соблюдение условия у > 0. [c.89]
МОНОТОННОЕ ПРЕОБРАЗОВАНИЕ [monotone transformation] — операция, производимая над некоторой упорядоченной совокупностью чисел таким образом, чтобы порядок их не изменился (при этом ни сами числа, ни интервалы между ними значения не имеют). Напр., при положительном М.п. вместо чисел 17, 35 и 68 можно получить 2,3,4 или 12,48,49, но нельзя 17, 11 и 13. Монотонными преобразованиями ряда положительных чисел являются умножение (или деление) каждого из них на одно и то же число, возведение в степень, извлечение корня и др. [c.207]
Порядковая Ш. (ordinal s ale) соответствует более высокому уровню шкалирования. Она предусматривает сопоставление интенсивности определяемого признака у изучаемых объектов (т.е. располагает их по признаку "больше—меньше", но без указания, насколько больше или насколько меньше). Порядковые Ш. широко используются при анализе предпочтений (отсюда термин "Ш. предпочтений") в различных областях экономики, но прежде всего в анализе спроса и потребления. Изучаемые объекты можно обозначить порядковыми числительными (первый, второй, третий), подвергая их любым монотонный преобразованиям (напр., возведению в степень, извлечению корня), поскольку первоначальный порядок этим не затрагивается. [c.394]
Монопсоническая власть (сила) 207 Монопсония 207 Монотонная функция 207 Монотонное преобразование 207 Монотонные функции полезности 380 Монте-Карло метод (метод статистических испытаний) 195 Морфологический анализ 207 Мощность аклератора 14 Мощность кода 146 Мультиколлинеарность 207 Мультимодальное распределение 202 Мультипликативная форма представления [c.475]
Функция FQ(/Q( )) = FQ( ) может оказаться выпуклой, хотя /о (С) и невыпукла, так как при монотонном преобразовании меняются наклон и кривизна при каждом С. Если удастся подобрать FQ так, чтобы обеспечить выпуклость FQ( ), то, как было показано выше, найдется такой вектор А, что абсолютный максимум в (9.105) окажется в точке С = 0. Это будет означать, что расширение (9.104) эквивалентно задаче НП по решению. Если это так, то можно определить решение задачи НП из условия седловой точки функции [c.347]
Рассмотрим изменение матрицы Гессе функции / (С) при ее монотонном преобразовании. Предварительно запишем составляющие градиента в точке [c.347]
Величина Ag+1 представляет собой значение задачи /ga после очередной итерации. Подчеркнем, что при использовании модифицированной функции Лагранжа этот прогноз, а значит и значение /О(ЖОА ), не учитывается при расчете А, здесь же вся информация, полученная при решении вспомогательной задачи (9.121), используется полностью. При тестовых расчетах алгоритмы, основанные на монотонном преобразовании функции /о в форме FQ(/Q — Ао)3 и / (ЛьАо) = = ar tg[(/o — АО)l/o — АО ] показали высокую эффективность. [c.365]
Позвольте нам начать с рационального объяснения первого типа выбора. Мы принимаем за очевидное, что индивид ведет себя логично, то есть у него совместимый набор предпочтений что эти предпочтения транзитивны, то есть если В предпочтительнее AtГ ч С предпочтительнее В, тогда С предпочтительнее А и что это предпочтение может быть полностью выражено просто приписыванием им численных значений. Смысл этих постулатов состоит в том, что выбор таких индивидов мы можем прогнозировать при помощи численной переменной (полезности). Опрашивая индивида с целью осуществить парное сравнение, мы задаем числа для надежных перспектив, так что порядок выбора будет определяться величиной заданных чисел. Количество парных сравнений, которые должен сделать индивид, зависит от того, насколько мы удачливы в отборе пар для его сравнения. Если нам посчастливится и мы сразу представим ему несколько пар выборов надежных перспектив, точно согласуя его порядок предпочтения, тогда полное упорядочение его предпочтений будет получено при минимальном количестве парных сравнений. Любая числовая последовательность, которая дает самую предпочтительную надежную перспективу, имеет наивысшую величину, следующая за ней по предпочтительности имеет второе по величине значение и т. д., и выбор будет прогнозироваться в соответствии с максимизацией полезности . Но любая другая последовательность чисел может быть использована до тех пор, пока она является монотонным преобразованием первой последовательности. И это точно отражает смысл утверждения, что полезность является порядковой, а не количественной. Постулат транзитивности дает возможность парному сравнению выявить полный порядок предпочтений, а постулат совместимости подразумевает, что он сделает свой выбор в соответствии с прогнозом. Таким образом, если бы ему нужно было представить какие-то две из десяти надежных перспектив, мы могли бы прогнозировать, что его выбор будет с наибольшей величиной полезности. Если наш прогноз не оправдывается, тогда следует отказаться от одного из наших постулатов, и наш метод прогнозирования не имеет силы. Скрытый постулат — это такой постулат, где предпочтения, [c.348]
Преимущество такого способа определения F состоит в том, что при монотонных преобразованиях вид функции принадлежности меняется не кардинально. Ее унимодальность или монотонность сохраняется, и переход от нового вида функции к словесной оценке, соответствующей некоторому квантификатору, происходит куда проще, чем от многогорбых функций, возникающих в результате операции суперпозиции. [c.145]
