Год Квартал Размер реализации, ед. Период, t Тренд, ед. Оценка сезонной компоненты аддитивной модели, ед. Оценка сезонной компоненты мультипликативной модели [c.185]
Итак, мы рассмотрели четыре способа выявления сезонной компоненты аддитивную модель, мультипликативную модель, метод экспоненциального сглаживания с тремя параметрами, гармонический анализ Фурье (рис. П-7). В нашем примере оказалось, что наименьшую ошибку дает мультипликативная модель, т. е. применение индексов сезонности. [c.439]
Кроме рассмотренных примеров аддитивных сезонных моделей, употребляются также и мультипликативные спецификации, например, [c.29]
Аддитивная модель, имеющая самостоятельную ценность в экономических исследованиях, интересна еще и тем, что позволяет строить модель с мультипликативной сезонностью и экспоненциальной тенденцией. Для этого необходима замена значений первоначального временного ряда их логарифмами, что преобразует экспоненциальную тенденцию в линейную и одновременно мультипликативную сезонную модель в аддитивную. [c.91]
Исходя из взаимосвязи компонентов между собой может быть построена аддитивная или мультипликативная модель ряда динамики ссудных процентов. Применение аддитивной модели предполагает, что характер циклических и сезонных колебаний остается постоянным и выражается следующей формулой [c.615]
Мультипликативная модель учитывает постоянный характер циклических и сезонных колебаний только по отношению к тренду и выражается уравнением [c.615]
Мультипликативная модель ряда динамики у = Т К S Е. В этой модели характер циклических и сезонных колебаний остается постоянным только по отношению к тренду. [c.78]
На основе поквартальных данных об уровне безработицы в летнем курортном городе (% от экономически активного населения) за последние 5 лет была построена мультипликативная модель временного ряда. Скорректированные значения сезонной компоненты за каждый квартал приводятся ниже [c.170]
Простейший подход — расчет значений сезонной компоненты методом скользящей средней и построение аддитивной или мультипликативной модели временного ряда. Общий вид аддитивной модели следующий [c.239]
Эта модель предполагает, что каждый уровень временного ряда может быть представлен как сумма трендовой (7), сезонной (S) и случайной ( ) компонент. Общий вид мультипликативной модели выглядит так [c.240]
Эта модель предполагает, что каждый уровень временного ряда может быть представлен как произведение трендовой (7), сезонной (S) и случайной ( ) компонент. Выбор одной из двух моделей осуществляется на основе анализа структуры сезонных колебаний. Если амплитуда колебаний приблизительно постоянна, строят аддитивную модель временного ряда, в которой значения сезонной компоненты предполагаются постоянными для различных циклов. Если амплитуда сезонных колебаний возрастает или уменьшается, строят мультипликативную модель временного ряда, которая ставит уровни ряда в зависимость от значений сезонной компоненты. [c.240]
Устранение сезонной компоненты из исходных уровней ряда и получение выравненных данных (Т+ Е) в аддитивной или (Г- Е)ъ мультипликативной модели. [c.240]
График данного временного ряда (рис. 5.6) свидетельствует о наличии сезонных колебаний (период колебаний равен 4) и общей убывающей тенденции уровней ряда. Прибыль компании в весенне-летний период выше, чем в осенне-зимний период. Поскольку амплитуда сезонных колебаний уменьшается, можно предположить существование мультипликативной модели. Определим ее компоненты. [c.245]
| Таблица 5.12 Расчет оценок сезонной компоненты в мультипликативной модели | 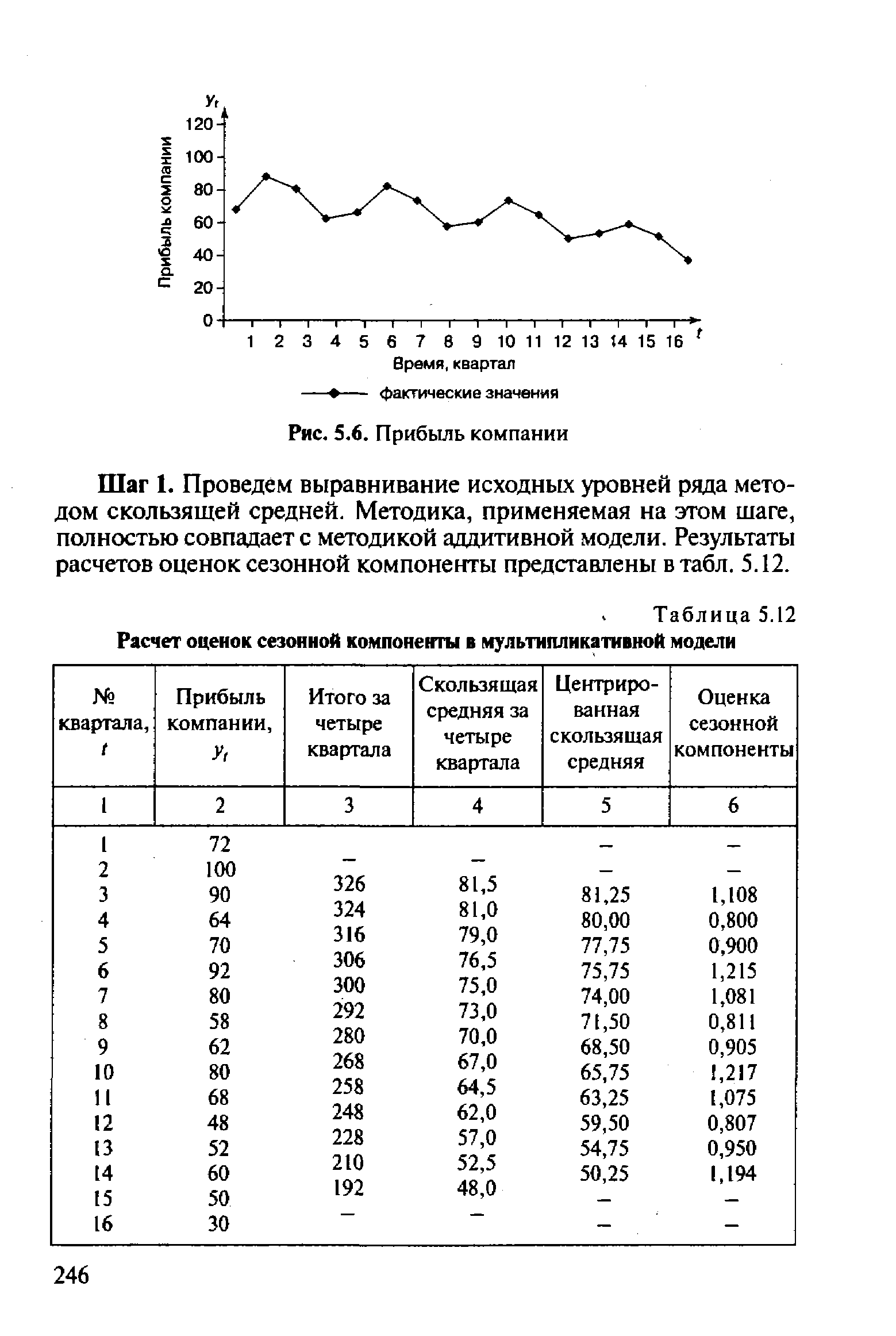 |
Прогнозное значение F, уровня временного ряда в мультипликативной модели в соответствии с соотношением (5.6) есть произведение трендовой и сезонной компонент. Для определения трендовой компоненты за каждый квартал воспользуемся уравнением тренда [c.251]
Устранение сезонной компоненты из уровней временных рядов можно проводить в соответствии с методикой построения аддитивной и мультипликативной моделей, рассмотренной в п. 5.4. При дальнейшем изложении методов анализа взаимосвязей в этой главе мы примем предположение, что изучаемые временные ряды не содержат периодических колебаний. Предположим, изучается зависимость между рядами х и у. Для количественной характеристики этой зависимости используется линейный коэффициент корреляции. Если рассматриваемые временные ряды имеют тенденцию, коэффициент корреляции по абсолютной величине будет высоким (положительным в случае совпадения и отрицательным в случае противоположной направленности тенденций рядов х и у). Однако из этого еще нельзя делать вывод о том, что х причина у или наоборот. Высокий коэффициент корреляции в данном случае есть результат того, что х и у зависят от времени, или содержат тенденцию. При этом одинаковую или противоположную тенденцию могут иметь ряды, совершенно не связанные друг с другом причинно-следственной зависимостью. Например, коэффициент корреляции между численностью выпускников вузов и числом домов отдыха в РФ в период с 1970 по 1990 г. составил 0,8. Это, естественно, не означает, что увеличение количества домов отдыха способствует росту числа выпускников вузов или увеличение числа последних стимулирует спрос на дома отдыха. [c.264]
Для мультипликативной модели (7.5) при первом варианте оценки тренда находится отношение фактических значений показателя к расчетным, определенным по трендовой модели. Во втором варианте оценки тренда находится отношение фактических значений показателя к скользящей средней (при нечетном т) или к центрированной средней (при четном /и). Такое отношение называется индексом (коэффициентом) сезонности. [c.182]
Если в аддитивной модели из фактического значения вычесть сезонную компоненту, а в мультипликативной модели фактическое значение разделить на индекс сезонности, то получим данные, в которых нет сезонности. [c.182]
Произведем оценку сезонной составляющей для мультипликативной модели (см. формулу 7.5) как отношение фактического размера реализации к значению тренда. Для t - 1 оценка сезонной компоненты равна 5, = 300/308,5 = 0,972. Для t = 2 s 2 = 300/310,4 = 1,031. Результаты определения сезонной составляющей для мультипликативной модели представлены в последнем столбце табл. 7.16. [c.184]
Рассмотрим мультипликативную модель прогноза. Рассчитаем средние индексы сезонности. Для первого квартала индекс сезонности равен [c.187]
Найдем случайную компоненту. Для этого фактические данные разделим на произведение значения тренда и сезонной компоненты (гр. 6 табл. П-10). Это абсолютная ошибка. Сумма квадратов ошибки составляет 56,1. Общая сумма квадратов отклонений значений исходного ряда от его среднего уровня составляет 63721,13. По отношению к общей сумме квадратов полученная сумма квадратов ошибки составляет 0,09% ( ). Следовательно, можно сказать, что мультипликативная модель объясняет 99,9% общей вариации уровней временного ряда отпущенных со склада единиц товара. [c.429]
Рассмотрим другой пример, в котором данные представлены поквартально. В табл. П-14 представлено определение оценок сезонной компоненты в аддитивной и мультипликативной моделях. Поскольку сезонные колебания имеют периодичность, равную 4 кварталам, в данном примере помимо определения скользящих средних требуется рассчитать центрированные значения средних. [c.439]
В табл. П-15 и П-16 показан расчет сезонной компоненты в аддитивной и мультипликативной модели соответственно. Значение корректирующего коэффициента в аддитивной модели равно (-0,365), в мультипликативной — 1,001. [c.439]
Точечная диаграмма (рис. 7.1.2) показывает, что объемы продаж имеют сезонные колебания и их значения в зимний период выше, чем в другие сезоны. Однако размах вариации постоянно возрастает, что указывает на необходимость применить модель с мультипликативной сезонной компонентой. [c.122]
Ряды производства животного масла и хлеба и хлебобулочных изделий (рис. 4.5) в первом приближении могут быть описаны мультипликативной моделью с неизменной сезонной волной. Поэтому для сезонной корректировки этих и подобных им рядов можно применять простейшие методы сезонной корректировки, предполагающие неизменность сезонных волн. Этот случай следует признать тривиальным. Для остальных восьми вре- [c.64]
В ситуации, когда сезонные волны эволюционируют, использование для сезонной корректировки простейших моделей с неизменной мультипликативной сезонной волной не представляется возможным, поскольку в этом случае на одних интервалах времени сезонная волна будет удаляться не полностью, а на других - с избытком. В результате часть сезонной волны (с [c.65]
Если в пунктах 2 и 5 под удалением понимается вычитание, то метод реализует аддитивную модель сезонности. При реализации мультипликативной модели под удалением из первого ряда второго понимается деление первого ряда на второй с последующим вычитанием из результата ряда единичных значений. [c.227]
Мультипликативная модель сезонности обычно используется для обработки рядов, у которых размах сезонных колебаний примерно пропорционален трендовой составляющей (как в рассмотренном примере). Если с изменением трендовой составляющей размах сезонных колебаний изменяется слабо, то лучше подходит аддитивная модель сезонности. [c.228]
В основе сезонных моделей лежат их несезонные аналоги, которые дополнены средствами отражения сезонных колебаний. Сезонные модели способны отражать как относительно постоянную сезонную волну, так и волну, динамически изменяющуюся в зависимости от тренда. Первая форма относится к классу аддитивных, а вторая - к классу мультипликативных моделей. Большинство моделей имеет обе эти формы. Наиболее широко в практике используются модели Хольта-Уинтерса, авторегрессии, модели Бокса-Дженкинса [15, 34]. [c.71]
Шаг 2. Найдем оценки сезонной компоненты как частное от деления фактических уровней ряда на центрированные скользящие средние (гр. 6 табл. 5.12). Используем эти оценки для расчета значений сезонной компоненты S (табл. 5.13). Для этого найдем средние за каждый квартал оценки сезонной компоненты 51,-. Взаимопогашаемость сезонных воздействий в мультипликативной модели выражается в том, что сумма значений сезонной компоненты по всем кварталам должна быть равна числу периодов в цикле. В нашем случае число периодов одного цикла (год) равно 4 (четыре квартала). [c.247]
Пятый этап — вычисление ошибки модели прогноза. Из фактического значения вычитаются сезонная компонента и тренд (аддитивная модель), для полученных остатков определяется среднее квадратиче-ское отклонение. В мультипликативной модели из фактического значения вычитается произведение индекса сезонности и тренда. По полученным остаткам также рассчитывается ошибка прогноза. Следует напомнить, что чем больше период упреждения прогноза, тем его точность будет меньше. [c.183]
Взаимопогашаемость сезонных воздействий в мультипликативной модели выражается в том, что сумма значений сезонной компоненты по отдельным периодам должна быть равна числу периодов в цикле. [c.187]
Модели с фиксированными переменными. Гармонические функции. Учет сезонных факторов в ARIMA. Адаптивные модели с мультипликативным и аддитивным эффектом сезонности. [c.86]
Так, производство теплоэнергии и топочного мазута (рис. 4.6) демонстрирует эволюцию сезонных волн. Хорошо видно, что до 1992г. (т. е. до начала переходного периода) размах сезонных колебаний производства теплоэнергии был примерно пропорционален уровню показателя, что допускало использование простейших моделей сезонной корректировки с неизменной мультипликативной сезонной волной. Однако, как это видно из рис. 4.6,а, после 1992г. такие модели перестали быть адекватными уровень показателя начал снижаться, а удельный размах сезонных колебаний увеличился (т. е. изменение масштаба сезонных колебаний не было пропорциональным изменению тенденции показателя). Ряд производства топочного мазута (рис. 4.6,6), напротив, демонстрирует уменьшение со временем удельного размаха сезонной волны. Таким образом, встречаются временные ряды, в которых сезонная волна эволюционирует как в сторону увеличения удельного размаха, так и в сторону его уменьшения, причем в условиях российского переходного периода первый тип эволюции сезонных волн являлся преобладающим на этапе доминирования тенденций спада, тогда как второй - на этапе доминирования тенденций роста. [c.65]
Аддитивная модель сезонности Тейла-Вейджа. В экономической практике чаще встречаются экспоненциальные тенденции с мультипликативно наложенной сезонностью. Поэтому перед использованием аддитивной модели члены анализируемого временного ряда обычно заменяют их логарифмами, преобразуя экспоненциальную тенденцию в линейную, а мультипликативную сезонность -в аддитивную. Преимущество аддитивной модели заключается в относительной простоте ее вычислительной реализации. Рассмотрим модель вида (в предположении, что исходные данные прологарифмированы) [c.54]
Используя данные таблиц Приложения Б, построить прогноз с использованием модели Уинтерса (экспоненциального сглаживания с мультипликативной сезонностью и линейным ростом). [c.90]
