Для проверки этой гипотезы разделим эмпирические данные на две группы по 350 точек с 1-й по 350-ю и с 467-й по 816-ю точки. Серединные точки с 351-й по 466-ю (14.2% от объема выборки) исключаем для лучшего разграничения между группами. Рассчитаем суммы квадратов ошибок для каждой из этих групп [c.152]
При сложении планируемых величин для нескольких работ суммарная ошибка составляет квадратичный корень из суммы квадратов ошибок по каждому виду работы. [c.42]
Кумулятивная сумма квадратов ошибок Se 100 104 273 .498 982 [c.24]
В табл. 1.2 дана типичная схема построения с помощью экспоненциально взвешенного среднего целочисленного прогноза ежемесячного спроса на некоторый товар. Значение константы экспоненциального сглаживания а была выбрано равным 0,2. На практике чаще всего а необходимо брать из интервала от 0,1 до 0,2. В некоторых программах для ЭВМ пользователю предоставляется возможность найти значение а исходя из минимума суммы квадратов ошибок. Для коротких временных рядов (как в табл, 1,2) более значимым представляется выбор начальной оценки прогноза. [c.25]
Покажите, что для данных из табл. 1.2 с начальным условием щ-г — 70 при а, = 0,If 0,3 и 0,4 значения суммы квадратов ошибок будут соответственно равны 2615, 2357 и 2212, Причина достаточно высокого оптимального значения а объясняется повышением спроса на товар, начиная с октября и далее. [c.26]
Теперь вместо составления и вычисления суммы квадратов ошибок, как при нахождении дисперсии, определим другую меру разброса, известную под названием среднее абсолютное отклонение ошибки (MAD,). Из названия следует, что среднее абсолютное отклонение есть просто абсолютное значение ошибки (отклонения). В гл. 1 было рассмотрено экспоненциально взвешенное среднее в качестве одной из форм среднего, поэтому нет причин не вычислять среднее абсолютное отклонение опять по формуле экспоненциально взвешенного среднего абсолютных значений ошибок [c.42]
Сумма квадратов ошибок 2е [c.56]
Используя данные табл. 5.1, при а = 0,2 по методу адаптивной скорости реакции (с лагом и без лага) постройте прогноз значений показателя покажите, что сумма квадратов ошибок прогноза по этим двум методам соответственно рав на 3176 и 1986. [c.65]
Критерий F в (13.20) при у = 0 имеет / -распределение с 1, (// — / — J) степенями свободы. Гипотезы НА и Нв проверяются так же, как в п. 13.3.2, только сумма квадратов ошибок определяется как СКе = ОСК — СКг и имеет на одну степень свободы меньше, чем в табл. 13.3. [c.387]
Кумулятивная сумма квадратов ошибок Se,2 1 1,04 4,43 6,74 9,91 10,09 [c.125]
Метод адаптивного сглаживания Брауна. Согласно второму методу Брауна, предполагается, что если ряд значений спроса можно описать некоторой моделью, то желательно применить регрессионный анализ на основе взвешенной регрессии, т. е. большее внимание необходимо уделять той информации, которая поступает позже. Данный метод основывается на простом способе вычисления оценок по методу минимизации взвешенной суммы квадратов ошибок прогноза в случае линейно-аддитивного тренда. Оценка по взвешенному методу наименьших квадратов равна [c.127]
На практике пригодность определяется функцией пригодности — блоком программы, который рассчитывает показатель относительной привлекательности решения. Функция может быть запрограммирована для определения пригодности именно так, как пожелает трейдер например, пригодность можно определять как общую прибыль за вычетом максимального падения капитала. Функция расходов устроена аналогично, но чем выше ее значение, тем хуже работает система. Сумма квадратов ошибок, часто вычисляемая при использовании систем с нейронными сетями или линейной регрессией, может служить примером функции расходов. [c.48]
Анализ (в смысле. математический или комплексный анализ) является расширением классического исчисления. Аналитические оптимизаторы используют наработанные методы, в особенности методы дифференциального исчисления и исследования аналитических функций для решения практических задач. В некоторых случаях анализ дает прямой (без перебора вариантов) ответ на задачу оптимизации. Так происходит при использовании множественной регрессии, где решение находится с помощью нескольких матричных вычислений. Целью множественной регрессии является подбор таких весов регрессии, при которых минимизируется сумма квадратов ошибок. В других случаях требуется перебор вариантов, например невозможно определить напрямую веса связей в нейронной сети, их требуется оценивать при помощи алгоритма обратного распространения. [c.57]
Сумма квадратов ошибок. Значения расстояний всех точек до линии регрессии возводят в квадрат и суммируют, получая сумму квадратов ошибок, которая является показателем общей ошибки [c.650]
Задавшись затем значением р, мы получим оценки р , р и р2, i процесс такого последовательного оценивания можно продолжать до ех пор, пока не будет достигнута сходимость с выбранной заранее точ-юстью. Некоторые эконометрики предпочитают комбинировать поиск итеративной процедурой, применяя поиск для решетки с очень широкими относительно р ячейками и выбирая в качестве начального значе-П1я р для итеративной процедуры тот узел решетки, который обеспе-шл наименьшее значение суммы квадратов ошибок. [c.318]
По аналогии с моделью регрессии для оценки качества построения модели или для выбора наилучшей модели можно применять сумму квадратов полученных абсолютных ошибок. Для данной аддитивной модели сумма квадратов абсолютных ошибок равна 1,10. По отношению к общей сумме квадратов отклонений уровней ряда от его среднего уровня, равной 71,59, эта величина составляет чуть более 1,5% [c.245]
Численные значения ошибки приведены в гр. 7 табл. 5.14. Если временной ряд ошибок не содержит автокорреляции, его можно использовать вместо исходного ряда для изучения его взаимосвязи с другими временными рядами. Для того чтобы сравнить мультипликативную модель и другие модели временного ряда, можно по аналогии с аддитивной моделью использовать сумму квадратов абсолютных ошибок. Абсолютные ошибки в мультипликативной модели определяются как [c.250]
В данной модели сумма квадратов абсолютных ошибок составляет 207,40. Общая сумма квадратов отклонений фактических уровней этого ряда от среднего значения равна 5023. Таким образом, доля объясненной дисперсии уровней ряда равна (1 - 207,40/5023) = 0,959, или 95,9%. [c.250]
Остаточная сумма квадратов по аддитивной модели (сумма квадратов абсолютных ошибок) была рассчитана ранее (табл. 5.10) и составляет 1,10. Следовательно, модель регрессии с фиктивными переменными описывает динамику временного ряда потребления электроэнергии лучше, чем аддитивная модель. [c.255]
Сумма квадратов абсолютных ошибок = 1,0981 [c.27]
Сумма квадратов абсолютных ошибок S Е = 1,0981 [c.28]
Для его вычисления отклонения по итоговым показателям по каждому признаку в отдельности возводятся в квадрат, полученные величины умножаются на соответствующие частоты, произведения суммируются, сумма делится на все число случаев, результаты уменьшаются на квадраты ошибок и из полученных чисел извлекается квадратный корень. [c.270]
Главная причина зависимости меры разброса от квадратов ошибок, а, например, не просто от суммы ошибок в том, что возведение в квадрат делает результат положительным вне зависимости от того, была ли первоначальная ошибка отрицательной или положительной. Для большинства прогнозов сумма ошибок стремится к нулю, т. е. положительные и отрицательные ошибки компенсируют одна другую. Вот почему сумма ошибок не может служить удовлетворительной мерой разброса. [c.42]
Метод, используемый чаще других для нахождения параметров уравнения регрессии и известный как метод наименьших квадратов, дает наилучшие линейные несмещенные оценки. Он называется так потому, что при расчете параметров прямой линии, которая наиболее соответствует фактическим данным, с помощью этого метода стараются найти линию, минимизирующую сумму квадратов значений ошибок или расхождений между величинами Y, которые рассчитаны по уравнению прямой и обозначаются Y, и фактическими наблюдениями. Это показано на рис. 6.2. [c.265]
После построения сети следует этап ее обучения (тренировки). На этапе обучения происходит подбор коэффициентов в формулах (2.4.1), (2.4.2) для нейронов сети. Эту процедуру можно назвать контролируемым обучением на вход сети подается вектор исходных данных, а сигнал на выходе сравнивается с известным результатом. Целью обучения является минимизация функции ошибок или невязки на множестве примеров путем выбора значений коэффициентов сети. Обычно в качестве меры погрешности берется средняя квадратичная ошибка, которая определяется как сумма квадратов разностей между истинной величиной выхода d k и полученными на сети значениями по всем Р примерам [c.144]
В ряде случаев проблема мультиколлинеарности может быть решена изменением спецификации модели либо изменением формы модели, либо добавлением объясняющих переменных, которые не учтены в первоначальной модели, но существенно влияющие на зависимую переменную. Если данный метод имеет основания, то его использование уменьшает сумму квадратов отклонений, тем самым сокращая стандартную ошибку регрессии. Это приводит к уменьшению стандартных ошибок коэффициентов. [c.252]
Сумма квадратов остатков е2 = е е является естественным кандидатом на оценку дисперсии ошибок а1 (конечно, с некоторым поправочным коэффициентом, зависящим от числа степеней свободы) [c.73]
Формально это записывается как минимизация суммы квадратов отклонений (ошибок) функции регрессии и исходных точек [c.112]
Эти два выражения показывают, как возникает ковариация между [52 и Рз в СИЛУ присутствия 2ыу в каждом из выражений для ошибок Р2 и (33. Положительное и большое значение ос приводит, как мы видим, к большим противоположным значениям ошибок J32 и(33- Если (32 оценивает значение р 2 снизу, то р3 оценивает значение ps сверху, и наоборот. Очень важным является то обстоятельство, что стандартные ошибки могут служить одним из индикаторов наличия мульти-коллинеарности. Формула (5.84) показывает, что истинное значение стандартной ошибки возрастает с увеличением а, однако эта формула содержит неизвестный параметр а . В оцененной величине стандартной ошибки значение а заменяется на Ее2/(п — /г), где 2е2 — сумма квадратов остатков после подгонки уравнения регрессии к эмпирическим данным. Как было показано в (5.19), [c.162]
| Рис. А.4. Блок-схема вычисления мер точности прогноза 1) суммы квадратов ошибок 2) среднего квадрата ошибок 3) средней ошибки 4) среднеа45сол отной процентной ошибки 5) средней лроцентной | 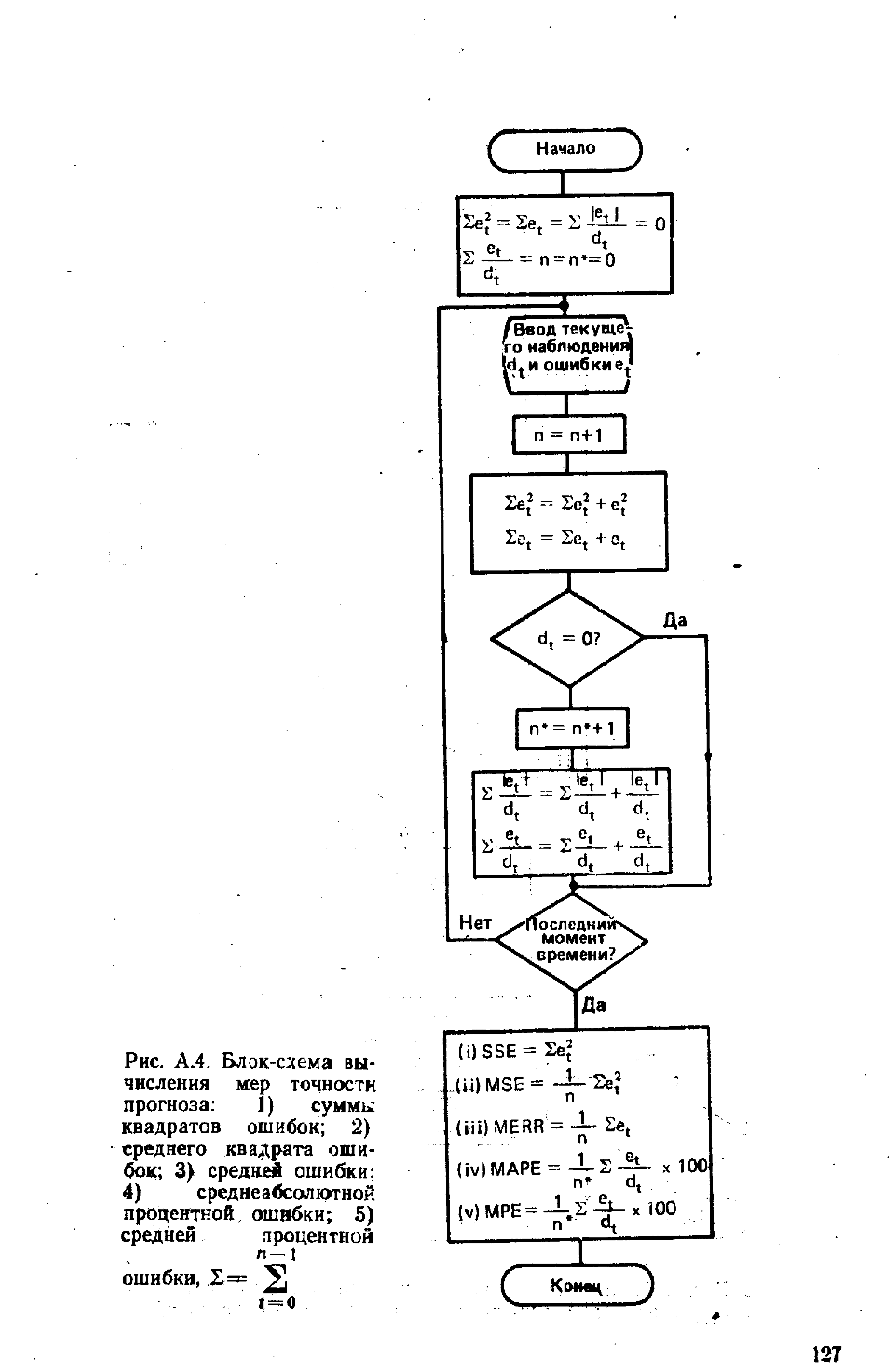 |
Частные производные от суммы квадратов разности по данному весу довольно легко вычисляются и оказываются пропорциональными расчетным ошибкам, полученным в ходе данной итерации. При этом расчетная ошибка нейрона выходного слоя пропорциональна фактической ошибке на его выходе, а расчетная ошибка нейрона слоя, предшествующего выходному, пропорциональна сумме ошибок всех нейронов выходного слоя, умноженных на соответствующие синаптические веса. Поэтому сначала вычисляют ошибки выходного слоя и определяют приращение весов его связей, а затем вычисляют ошибки предыдущего слоя и вычисляются веса его связей и так корректируются все веса по направлению от входа к выходу. Поэтому такой алгоритм и назван [c.132]
При выполнении предпосылок 1)-4) относительно ошибок е( оценки параметров множественной линейной регрессии являются несмещенными, состоятельными и эффективными. Отклонение зависимой переменной у ву-м наблюдении от линии регрессии, ер записывается следующим образом е = у - а0 - atx - a fl -. .. - amxjm. Обозначим сумму квадратов этих величин, которую нужно минимизировать в соответствии с методом наименьших квадратов, через Q. [c.308]
Возникает естественный вопрос, при каких обстоятельствах можно пользоваться описанным выше методом. Ниже будут описаны некоторые процедуры, позволяющие выявлять гетероскеда-стичность того или иного рода (тесты на гетероскедастичность). Здесь мы ограничимся лишь практическими рекомендациями. Если есть предположение о зависимости ошибок от одной из независимых переменных, то целесообразно расположить наблюдения в порядке возрастания значений этой переменной, а затем провести обычную регрессию и получить остатки. Если размах их колебаний тоже возрастает (это хорошо заметно при обычном визуальном исследовании), то это говорит в пользу исходного предположения. Тогда надо сделать описанное выше преобразование, вновь провести регрессию и исследовать остатки. Если теперь их колебание имеет неупорядоченный характер, то это может служить показателем того, что коррекция на гетероскедастичность прошла успешно. Естественно, следует сравнивать и другие параметры регрессии (значимость оценок, сумму квадратов отклонений и т. п.) и только тогда принимать окончательное решение, какая из моделей более приемлема. [c.170]
Пусть теперь Е( ) = О Q, где Q - вещественная, симметрическая положительно определенная матрица (структура ковариации ошибок). Обобщенный метод наименьших квадратов (ОМНК), приводящий к оценкам класса BLUE, означает минимизацию взвешенной суммы квадратов отклонений [c.27]
Чтобы сделать определенным анализ системы уравнений, предполагаемой уравнением (3.25), допустим, что NS - это положения ПВ, NR - положения сейсмоприемни-ков, NG - положения ОСТ. Определим кратность как NF. Задача состоит в том, чтобы разложить наблюденные времена пробега, оцененные (пикированные) по данным ( уй) на составляющие, как определено в правой части уравнения (3.25). Количество пиков времени (или отдельных уравнений) равно NG x NF. Количество неизвестных равно NS + NR + NG + NG. Обычно NG x NF > NS + NR + NG + NG количество уравнений превышает количество неизвестных. Это задача наименьших квадратов, в которой мы должны минимизировать сумму энергии ошибок наименьших квадратов между наибольшими пиками t ijh и смоделированными временами t [c.49]
